P10789 [NOI2024] 登山 解题报告

Tag：DP，DP 优化。

大约 \(3\text{ months}\) 之前开了这个题，发现自己一点也不会，遂弃之，现在才来补。

\bx\bx\bx jg。

做法来源于：《题解：P10789 [NOI2024] 登山》——Larunatrecy。

一开始看了看出题人题解，你的方法小众又独特。这老哥把前面的 Subtask 都讲得很清楚，但是你倒是告诉我怎么做线段树合并的逆啊？？呜呜呜哭菜。

Statement

题意简述：有一棵以 \(1\) 为根的有根树，需要计算出以每个 \(i\) 为起点，\(1\) 为结尾的攀登序列的方案数，其中攀登过程可以由攀登或下滑（仅当可下滑时）构成。对于攀登，对每个节点给出了攀登步数区间 \([l_i,r_i]\)，且给出 \(lim_i\)，要求对于每次攀登其节点深度 \(dep_i<\) 前面所有访问过节点的 \(dep_j-lim_j\)。

Analysis

为了方便，我们先记 \([l_i,r_i]\) 表示能爬到的深度区间，并记 \(lim_i\) 表示至少要爬到的深度最大值。发现我们的操作可以是若干次下滑 + 一次攀登循环组成。即每次找到点 \(i\)，往下滑到子树内点 \(j\)（\(j\) 可能 \(=i\)，即不滑），然后再跳到 \(i\) 的某个祖先 \(k\)。

由于在 \(j\) 往上跳，\(k\) 当然要满足 \(dep_k\in[l_j,r_j]\)。同时我们发现跳到一个新节点后，其 \(lim_k\) 一定 \(<\) 之前所有节点最小的 \(lim_j\)。于是对于下一次跳跃，我们只需要计算下滑的那一段的 \(lim\) 的 \(\min\)，并且对深度区间加以限制。不妨令 \(v_{i\to j}\) 表示 \(i\to j\) 路径上 \(lim\) 的 \(\min\)，则有：\(dep_k\in[l_j,\min(r_j,v_{i\to j})]\)。

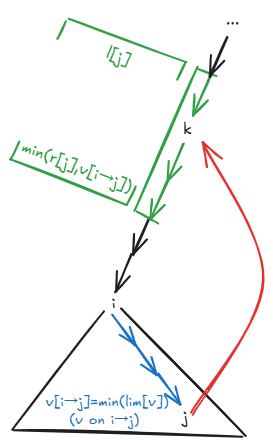
这样从上至下 DP，设 \(f_i\) 表示以 \(i\) 为起点的合法登山序列数量，每次在 \(i\) 子树中枚举 \(j\) 把一段祖先链 \(k\) 加到 \(i\) 上即可解决。使用祖先链上前缀和优化一下转移时间复杂度 \(\Theta (n^2)\)。

发现我们优化时间的瓶颈主要在于我们 \(k\to i\) 的转移实际上依赖 \(i\) 子树内的节点 \(j\)。不妨换个角度思考，让 \(j\) 去找 \(i\)，把其对 \(i\) 的贡献直接变成一个前缀和的形式：\(s_{\min(r_j,v_{i\to j})}-s_{l_j-1}\)。考虑 \(-s_{l_j-1}\)，发现此时 \(j\) 贡献到的 \(i\) 是一段后缀，且链首的父亲是第一个 \(lim_i < l_j\) 的 \(i\)，这个离线下来简单链加单点查即可解决。（树状数组 + DFS 序解决链加单点查：查询时查子树信息，单点加 DFS 序对应位置）

考虑解决 \(s_{\min(r_j,v_{i\to j})}\)，发现这个东西难处理在它有个 \(\min\)，导致它能贡献到的 \(i\) 会动态变化（但总是一段后缀）。考虑拆掉这个 \(\min\)，发现可以分为：

1. \(r_j\le v_{i\to j}\)，此时直接取 \(s_{r_j}\)，可以贡献到的 \(i\) 是一段固定后缀。

2. \(r_j > v_{i\to j}\)，此时我们不妨让那个取到 \(lim_u=v_{i\to j}\) 的点 \(u\) 为我们代替 \(j\) 向 \(i\) 贡献。由于可能有多个，我们取其中最深的那个，能贡献到的 \(i\) 是以 \(u\) 为结尾的一段后缀。

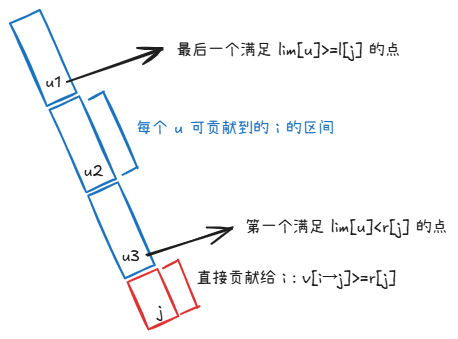
如何处理这个东西？瓶颈在快速找到所有 \(u\)。发现可以对于每个 \(i\) 都找到第一个 \(<lim_i\) 的点 \(lim_{fa}\)，然后 \(fa\to i\) 连边可以形成一棵树（以 \(0\) 为根），然后 \(j\) 能找到的所有 \(u\) 构成该树上的一个后缀，也是链加然后计算出对于每个 \(u\) 有多少对应的 \(j\) 数量为 \(w_u\)。

有了 \(w_u\)，我们发现此时 \(u\) 能贡献到的点与 \(j\) 无关，而是与 \(lim_u\) 直接相关。因为 \(u\) 需要作为 \(i\to j\) 上第一个取到最小值的点，所以其最浅作用节点就截至到第一个取到 \(lim_k < lim_u\) 的 \(k\) 前（不包含）。然后在 \(u\) 链加单点查即可。

考虑消除转移后效性，需要把每个需要 \(s_u\) 信息的转移离线下来，等到处理好 \(f_u,s_u\) 后再去链加后面的点。这样做是 \(O(n\log n)\) 的。

Summary

总结：我们在题目中做出了几步关键转化：

1. \(lim\) 的限制在攀登时收紧，因此只需考虑最新取到的 \(lim\)。

2. 贡献转祖先链上前缀和，使得消除链查的可能。

3. 找到后缀最小值 \(u\)，因为取到了该节点就可以取到这个最小值，限制最紧。

4. 拆 \(\min\)，自己能贡献的自己贡献，否则给第一个取到 \(\min\) 的 \(u\) 贡献。

附赠一组样例图片：

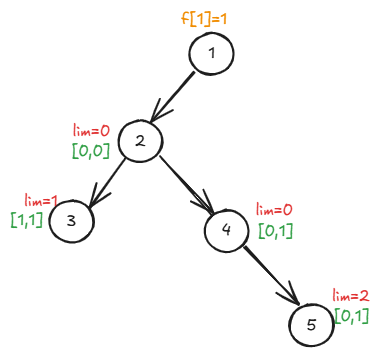
点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD=998244353;
const int N=1e5+5;
int n,dfn[N],tms,fat[N],siz[N];
int lim[N],dep[N],L[N],R[N];
int rfat[N],stk[N],tp,w[N];
int mn[N][18],up[N][18];
LL s[N],f[N];
vector<int>G[N],rG[N];
struct Q{int L,R,v;};
vector<Q>op[N];
int qcnt;
struct BIT{
	LL av[N];
	inline int lowbit(int x){return x&-x;}
	void init(){for(int i=1;i<=n;i++)av[i]=0;}
	void add(int p,LL x){
		if(!p)return ;
		for(int i=p;i<=n;i+=lowbit(i))
			(av[i]+=x)%=MOD;
	}
	LL que(int p){
		LL res=0;
		for(int i=p;i;i-=lowbit(i))
			(res+=av[i])%=MOD;
		return res;
	}
}T;
void init(){
	T.init();qcnt=tms=0;
	for(int j=0;j<=17;j++)
		mn[0][j]=-1;
	rG[0].clear(); 
	G[0].clear();
	for(int i=1;i<=n;i++){
		w[i]=f[i]=s[i]=0;
		G[i].clear();
		rG[i].clear();
		op[i].clear();
		for(int j=0;j<=17;j++)
			mn[i][j]=-1,up[i][j]=0;
	}
	f[1]=s[1]=1;
}
inline int findlast(int u,int k){
	if(lim[u]<k)return u;
	for(int i=17;i>=0;i--)
		if(up[u][i]&&mn[u][i]>=k)
			u=up[u][i];
	return u;
}

void dfs0(int u){
	dfn[u]=++tms;
	w[0]=0;siz[u]=1;
	for(int v:G[u]){
		up[v][0]=u;
		mn[v][0]=lim[u];
		for(int j=1;(1<<j)<=dep[u]+1;j++)
			up[v][j]=up[up[v][j-1]][j-1],
			mn[v][j]=min(mn[v][j-1],mn[up[v][j-1]][j-1]);
		dfs0(v);siz[u]+=siz[v];
	}
}

inline int findw(int k){
	int l=1,r=tp,res=tp;
	while(l<=r){
		int mid=(l+r)>>1;
		if(lim[stk[mid]]>=k)res=mid,r=mid-1;
		else l=mid+1;
	}
	return stk[res];
}
void dfs1(int u){
	stk[++tp]=u;
	if(u&&u!=1&&lim[u]>=L[u]){
		int p1=findw(L[u]),
		 p2=findw(R[u]);
		 if(lim[p2]>=R[u])p2=rfat[p2];
		w[p2]++;w[rfat[p1]]--;
	}
	for(int v:rG[u]){
		dfs1(v);
		w[u]+=w[v];
	}
	stk[tp--]=0;
}
void dfs2(int u){
	stk[tp++]=u;
	int fa=fat[u];
	if(w[u])op[stk[lim[u]]].emplace_back(Q{findlast(u,lim[u]),u,w[u]});
	if(lim[u]>=L[u]&&L[u]>=1)
		op[stk[L[u]-1]].emplace_back(Q{findlast(u,L[u]),u,-1});
	if(lim[u]>=R[u])
		op[stk[R[u]]].emplace_back(Q{findlast(u,R[u]),u,1});
	for(int v:G[u])
		dfs2(v);
	stk[--tp]=0;
}
void dfs(int u){
	int fa=fat[u];
	if(u!=1){
		f[u]=(T.que(dfn[u]+siz[u]-1)-T.que(dfn[u]-1)+MOD)%MOD; 
		s[u]=(s[fa]+f[u])%MOD;
	}
	for(Q v:op[u]){
		int l=v.L,r=v.R,val=v.v;
		T.add(dfn[r],(val*s[u]%MOD+MOD)%MOD);
		T.add(dfn[fat[l]],(-val*s[u]%MOD+MOD)%MOD); 
	}
	for(int v:G[u])
		dfs(v);
}
int main(){
	//freopen("mountain.in","r",stdin);
	//freopen("mountain.out","w",stdout);
	int Cn,Tn;scanf("%d%d",&Cn,&Tn);
	while(Tn--){
		scanf("%d",&n);
		init();
		for(int i=2;i<=n;i++){
			int l,r,h;
			scanf("%d%d%d%d",&fat[i],&l,&r,&h);
			G[fat[i]].emplace_back(i);
			dep[i]=dep[fat[i]]+1;
			lim[i]=dep[i]-h-1;
			swap(l,r);
			L[i]=dep[i]-l;
			R[i]=dep[i]-r;
		}
		dfs0(1);
		for(int i=1;i<=n;i++){
			int fd=findlast(i,lim[i]);
			rfat[i]=fat[fd];
			rG[fat[fd]].emplace_back(i);
		}
		dfs1(0);
		dfs2(1);dfs(1);
		for(int i=2;i<=n;i++)
			printf("%lld ",f[i]);
		printf("\n");
	}
	return 0;
}