Paper | Contrast Limited Adaptive Histogram Equalization
Contrast Limited Adaptive Histogram Equalization
1. 背景
1.1. 对比度和直方图均衡HE
“对比度contrast ratio”这一概念,类似于“动态范围dynamic range”,衡量的是图像中亮区与暗区的比例。
对比度实际上没有统一的测量标准,参见:维基百科
但我们知道,对比度是影响图像视觉效果的重要因素。
对比度小的图像,其色彩层次少,看起来要么太亮,要么太暗。如下图(太暗):

实际上摄影师是为了追求这种效果啦,但我们还是拿来做一个demo。
利用MATLAB内置的histeq函数,可以得到对比度增强的图片:
img=imread('Cloudy Night View.jpg');
rimg=img(:,:,1);
gimg=img(:,:,2);
bimg=img(:,:,3);
resultr=histeq(rimg);
resultg=histeq(gimg);
resultb=histeq(bimg);
result=cat(3,resultr,resultg,resultb);
imwrite(result,'result.jpg')

图像清晰了太多有没有!!!很多隐藏的细节都被挖掘出来了。
当然,这个结果有些色彩失真。我们尝试在Lab color space上进行,据说是最接近人眼特性的色彩空间:
cform2lab = makecform('srgb2lab');
imgLAB = applycform(img, cform2lab);
L = imgLAB(:,:,1);
imgLAB(:,:,1) = histeq(L);
cform2srgb = makecform('lab2srgb');
result2 = applycform(imgLAB, cform2srgb);
imwrite(result2,'result2.jpg')

可以看到,色彩失真有所改善。
直方图均衡的本质是灰度值映射。而映射函数可以由分布曲线(累积直方图)得到:
其中 \(A_0\) 是像素总数(图像面积),\(D_{max}\) 是最大灰度值,\(D_A、D_B\) 分别是转换前、后的灰度值,\(H_i\) 是第 \(i\) 级灰度的像素个数。
例如原直方图为:

-
灰度值0到120,累积像素个数都为0,因此灰度值0到120都映射到灰度值0;
-
此后黑线开始上升,其纵坐标就是映射到的灰度值(当然还有系数 $ \frac {D_{max}}{A_0} $ )。
-
灰度值200左右,黑线饱和,因此其后的灰度值都映射到最大灰度值255。
经过均衡后的直方图为:

综上,HE后的直方图实际上是原直方图的拉伸,只是左右拉伸程度是变化的,取决于原直方图的幅度变化。
参见:维基百科 histogram equalization
1.2 HE的问题
以上是直方图均衡Histogram Equalization的简单应用。事实上,HE最初用在医疗图像上。以下图为例:
如果只应用简单的HE,结果如图:
尽管组织“点亮”了,但底噪一样被“点亮”了。
1.3 AHE
在CLAHE提出以前,学者还提出了自适应直方图均衡Adaptive Histogram Equalization。
AHE的思想很简单:"Since our eyes adapt to the local context of images to evaluate their contents, it makes sense to optimize local image contrast (Pizer et al. 1987)."
大体上是:为了改善局部对比度,我们采用块操作。此时HE在每一个块上都会最优,从而实现各个局部最优。进一步,为了避免边界效应,我们组合块时采用双线性插值法,而不是简单的合并。
根据实验结果,AHE在目标区域表现比HE更出色,但底噪问题仍然没有解决。
1.4 底噪问题
我们思考一下底噪问题的本质。
不妨考虑极端情况。假设原直方图中只有一个柱子,对应灰度值为0。这就是说,这本应该是一个全黑的块。
然鹅,根据HE原理,由于灰度值0处
因此灰度值0的柱子变成了灰度值255的柱子,整幅图像变成了全1阵(为什么是1不是255?这里涉及到MATLAB图像格式的问题,不赘述)。即,全黑图像变成了全白图像。

因此,我们应该限制分布函数cumulative distribution function的斜率。
大斜率导致低灰度值映射到高灰度值,使原本集中的黑色背景“点亮”。这就是CLAHE的根本思想。
2. CLAHE
2.1 效果展示
References:
Karel Zuiderveld, "Contrast Limited Adaptive Histogram Equalization", Graphics Gems IV, p. 474-485, code: p. 479-484
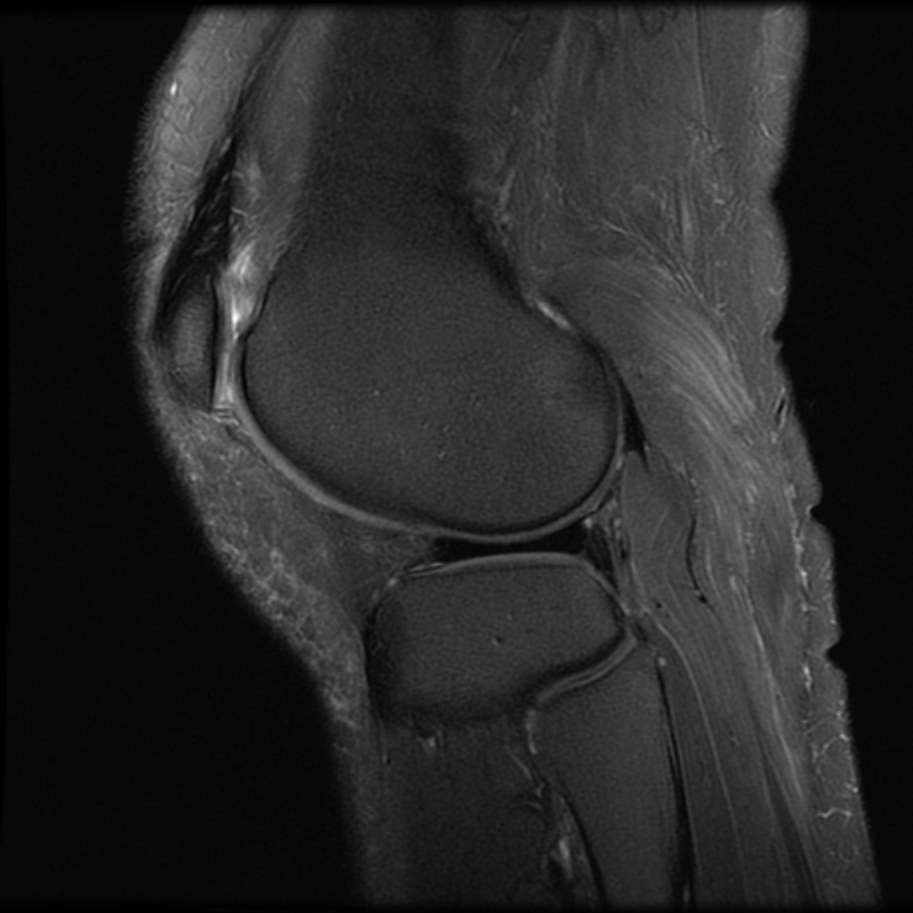
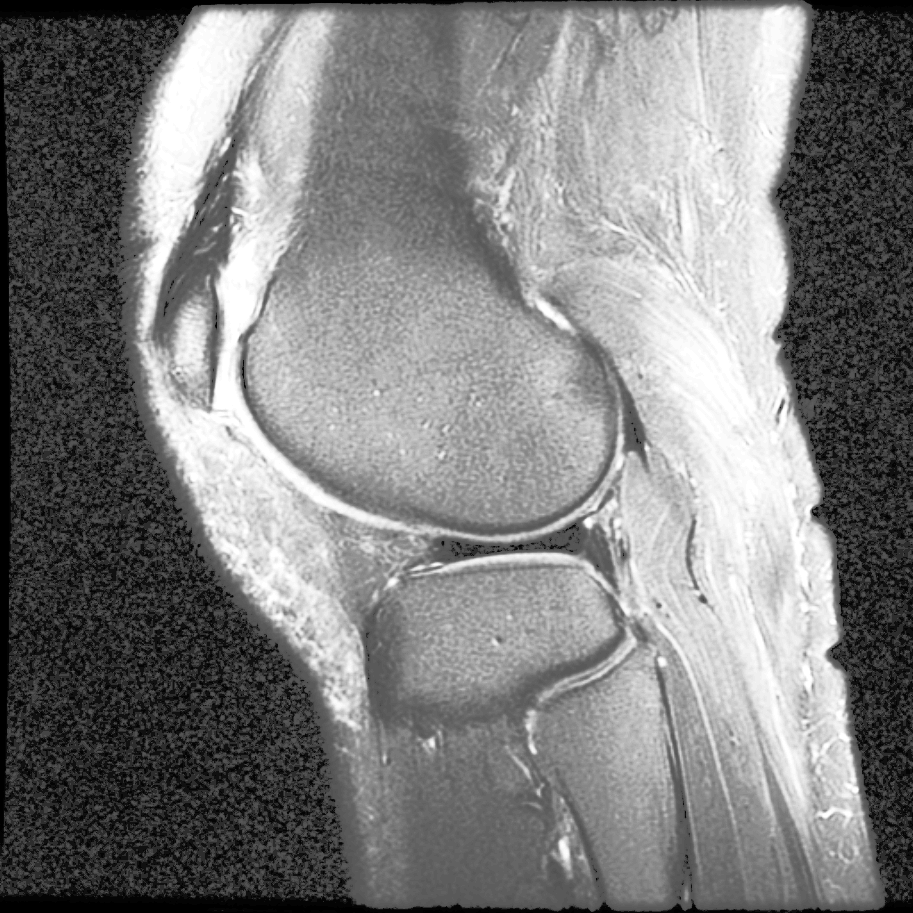
MATLAB内置了adapthisteq函数,可以实现CLAHE算法。我们以Human Knee为例,看看CLAHE效果:
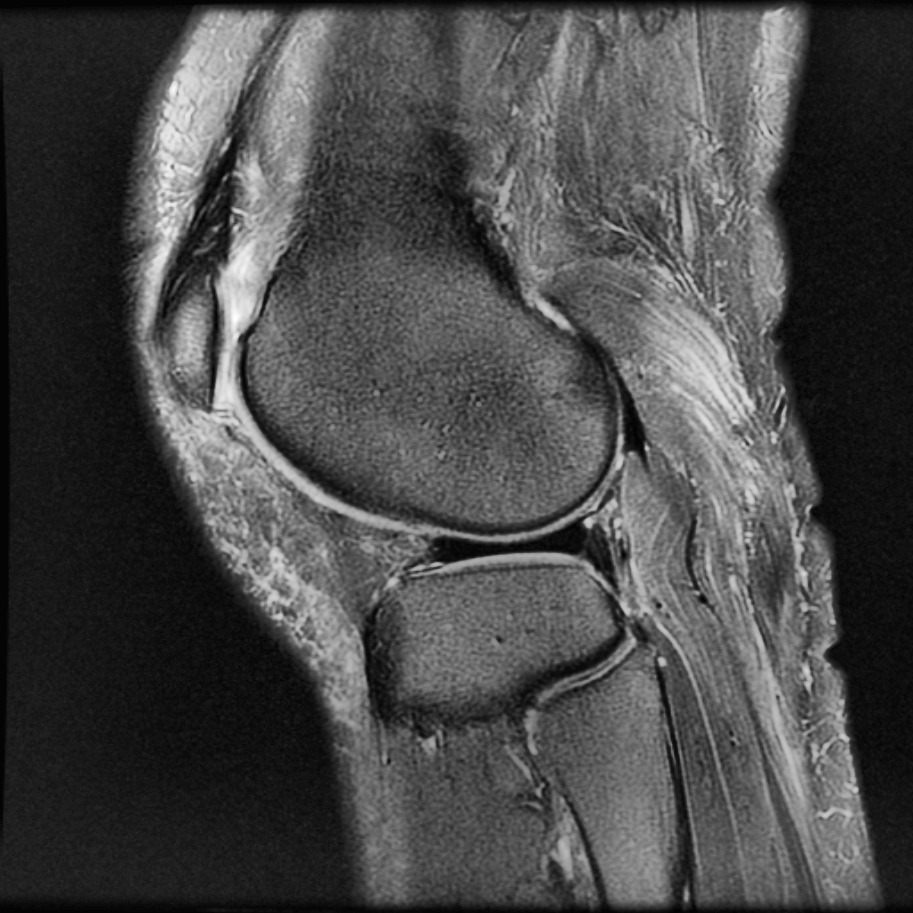
不仅目标被点亮了,而且低噪也被抑制了!
2.2 算法格式和细节
原作中给出的是C语言程序实现。这里我们研究MATLAB内置函数adapthisteq的源代码。
函数的输入方式有两种:
J = ADAPTHISTEQ(I)
J = ADAPTHISTEQ(I,PARAM1,VAL1,PARAM2,VAL2...)
显然第一种使用的是默认参数。
参数有:
-
NumTiles:是一个[M N]行向量,表征tile的行和列数。默认8x8。最好通过实验确定。
-
ClipLimit:0到1的一个标量,表征最大最大clip。显然是归一化的。默认0.01。如果太大,CLAHE退化为AHE。
-
NBins:输出图像直方图的柱子个数。因此输入图像和输出图像的位数不一定相同,NBins越大,动态范围越大,但速度越慢。默认为256。
-
Range:要么是'original',要么是'full'。前者限制变换范围在[min(I(😃) max(I(😃)],后者是整个允许范围。默认为full。
-
Distribution:每一个tile的直方图的目标。'uniform', 'rayleigh', 'exponential'。默认为均衡分布'uniform'。对于水下图片,瑞利分布更自然。
-
Alpha:非负标量,在瑞利分布和指数分布时使用。
为了简化计算,以及避免边界效应,这里只计算了每一个tile的cluster,其余像素点使用了插值的方法:
% 4. Interpolate gray level mappings in order to assemble final CLAHE image
% * extract cluster of four neighboring mapping functions
% * process image region partly overlapping each of the mapping tiles
% * extract a single pixel, apply four mappings to that pixel, and
% interpolate between the results to obtain the output pixel; repeat
% over the entire image
原文说明:



