[SDOI2012] 任务安排

[SDOI2012] 任务安排

斜率优化 dp 裸题。

题意

给定 \(n\) 个任务，每个任务有一个时间 \(T_i\) 和一个费用系数 \(C_i\)。

你需要将 \(n\) 个任务划分成若干非空连续段，从时刻 \(0\) 开始，依次执行每段任务。

对于每段任务，令其对应任务编号为 \([l,r]\)，则其首先需要 \(S+\sum_{i=l}^{r}T_i\) 的时间准备，然后瞬间完成编号在 \([l,r]\) 内的所有任务。

我们定义任务 \(i\) 的费用是其完成时刻 \(end_i\) 与其费用系数 \(C_i\) 的乘积，求所有任务费用的最小值。

其中 \(1 \leq n \leq 3 \times 10^5\)，\(1 \leq S \leq 2^8\)，\(0 \leq C_i \leq 2^8\)，\(|T_i| \leq 2^8\)，注意 \(T_i\) 可以为负，也就是说完成某些任务可以让时光倒流。

思路

首先我们考虑最朴素的 dp。我们令 \(dp_{i,j}\) 表示对于前 \(i\) 个任务划分为 \(j\) 段的最小费用。那么我们有下面的转移方程：

\[dp_{i,j}=\min_{0 \leq k < i} \{dp_{k,j-1}+(S \times j+\sum_{l=1}^{i}T_l) \times \sum_{l=k+1}^{i} C_l\} \]

这个做法是 \(O(n^3)\) 的，显然不可通过。

dp 中记录 \(j\) 的根本目的是为了 \(S\) 贡献的加权。单独考虑 \(S\) 的加权，就会发现其应该是其后所有任务费用和。

所以我们去掉一维，就有下面的转移方程：

\[dp_i=\min_{0 \leq j < i} \{dp_j+S \times \sum_{k=j+1}^{n}C_k+\sum_{k=1}^{i}T_k \times \sum_{k=j+1}^{i} C_k\} \]

现在已经是 \(O(n^2)\) 了，考虑继续进行优化。

首先我们可以求出 \(C\) 和 \(T\) 的前缀和数组，记为 \(sumc\) 和 \(sumt\)，那么方程化为：

\[dp_i=\min_{0 \leq j < i} \{dp_j+S \times (sumc_n-sumc_j)+sumt_i \times (sumc_i-sumc_j)\} \]

为了方便，我们转化为数组的形式：

\[dp[i]=\min_{0 \leq j < i} \{dp[j]+S \times sumc[n]-S \times sumc[j]+sumt[i] \times sumc[i]-sumt[i] \times sumc[j]\} \]

提出一些常量，可得：

\[dp[i]=S \times sumc[n]+sumt[i] \times sumc[i]+\min_{0 \leq j < i} \{dp[j]-S \times sumc[j]-sumt[i] \times sumc[j]\} \]

我们令 \(k=S+sumt[i]\)，则可得：

\[dp[i]=(S \times sumc[n]+sumt[i] \times sumc[i])+\min_{0 \leq j < i} \{dp[j]-k \times sumc[j]\} \]

\(dp[j]-k \times sumc[j]\) 长得很像直线，所以我们令直线 \(l\) 经过点 \((sumc[j],dp[j])\) 且斜率为 \(k\)，则其截距就是 \(dp[j]-k \times sumc[j]\)。

所以我们动态维护平面上的点集 \((sumc[i],dp[i])\)，则需要维护两个操作：

• 加入一个点

• 对每个点画一条斜率为 \(x\) 的直线，询问截距的最小值。

在这个过程中，很容易发现一个关键的性质，，即加入的点横坐标一定单调递增。

其次，在第二个操作中，我们发现只有下凸壳上的点有可能会产生答案。

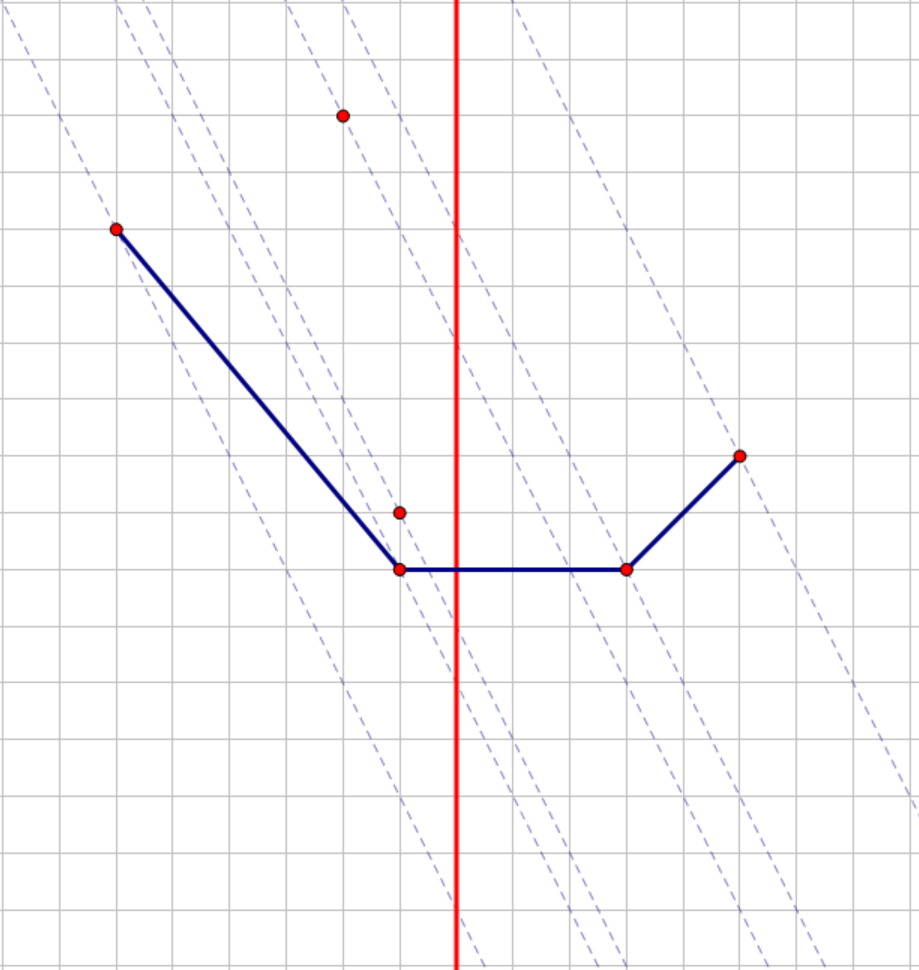
如图，这是斜率优化的重要性质。因为加入的点横坐标单调递增，所以可以使用单调栈维护下凸壳。

对于操作二，我们可以二分斜率解决。

然后这道题目就结束了，属于是入门斜率优化 dp 了。

代码

#include<iostream>
#include<cstdio>
using namespace std;
long long T[300010],C[300010],sumt[300010],sumc[300010],dp[300010];
int st[300010],top;
long long query(long long slope){
	int l=1,r=top;
	while(l<r){
		int mid=(l+r)>>1;
		if((dp[st[mid+1]]-dp[st[mid]])>=slope*(sumc[st[mid+1]]-sumc[st[mid]])){
			r=mid;
		}
		else{
			l=mid+1;
		}
	}
	return dp[st[l]]-slope*sumc[st[l]];
}
int main(){
	int n;
	long long S;
	scanf("%d %lld",&n,&S);
	for(int i=1;i<=n;i++){
		scanf("%lld %lld",&T[i],&C[i]);
		sumt[i]=sumt[i-1]+T[i];
		sumc[i]=sumc[i-1]+C[i];
	}
	st[++top]=0;
	for(int i=1;i<=n;i++){
		dp[i]=S*sumc[n]+sumt[i]*sumc[i]+query(S+sumt[i]);
		while(top>=2  &&  (dp[st[top]]-dp[st[top-1]])*(sumc[i]-sumc[st[top]])>=(dp[i]-dp[st[top]])*(sumc[st[top]]-sumc[st[top-1]])){
			top--;
		}
		st[++top]=i;
	}
	printf("%lld",dp[n]);
	return 0;
}