BUAA_OO_第三单元总结

OO第三单元总结

第三单元要求了解JML语法和语义，并根据JML给出的规格编写代码，从而实现一个简单的社交关系模拟和查询系统，关键在于要准确的理解JML规格。

一、架构设计与算法性能优化

整体图模型建构

这一单元作业的背景是一个社交网络，层次有三层：Network，Group和Person，本质就是一个图，其中每一个person就是一个节点，relation就是节点之间的边，Network中的一系列方法都是用来维护这个图的方法，在完成Network中的方法时也借助了很多数据结构时所学的关系到图的算法。

关于Network中方法的实现，当然最准确和最保险的策略就是仔细阅读JML规格，一句一句翻译实现，只要与JML一模一样就一定不会出错，但是这并不是最好的策略。对于简单的方法这样做没有大问题，但是像isCircle等这些方法，JML规格有几十行长，而且全部都是括号的嵌套，要全部读懂真的很费劲。

所以在完成这一单元的作业时，我更倾向于先理解再下手，因为这次实现的就是一个社交网络，里面的很多功能其实与现实生活中是很像的，比如发送消息、发送表情包、存表情包这一系列的操作……所以我采用的方法时，首先弄明白已给出的各个类之间的关系，明白person和relation这些边与节点之间的关系，然后看方法名猜功能，首先思考这个方法要干什么，与现实生活里的场景（比如发微信）相联系，思考实现这个方法的必要性与意义。当自己对这个功能大致有一个认识之后，再读JML进行验证以及补充完善，这样能大大的减少花费在阅读JML上的时间。

容器选择

为了使用访问更加方便，我使用了HashMap作为容器，如MyPerson的acquaintance，MyNetwork的people、groups、messages等属性。

除此之外，Hashmap中的key与value属性也可以自行构造类来代替，这样更有灵活性。

hw9

UML图

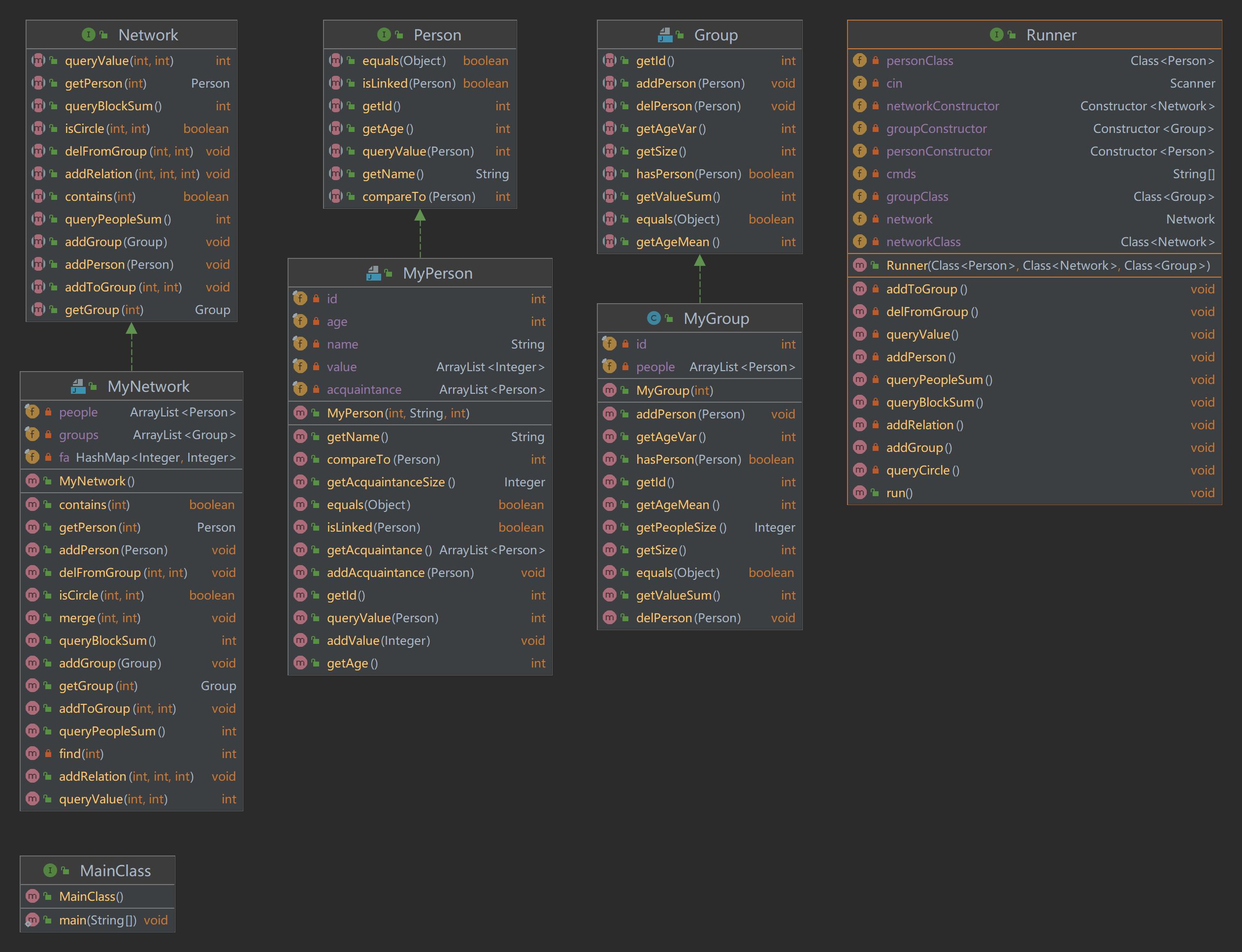
路径压缩并查集

针对isCircle方法，拒绝了dfs：本身时间复杂度就高，queryBlockSum按照规格的实现方法甚至还会调isCircle，风险较大。

为了降低时间复杂度，所以选取了讨论区助教提供的并查集方法，具体实现与助教讨论曲中给出的思路一致，建立find与merge的方法。

但是我在进行路径压缩优化的时候遇到了一点问题。

我第一次实现的find方法是这样的，这里面fa是一个HashMap类型的，key存储的是节点的id，value存储的是节点父节点的id：

public int find(int id) {
    int father = fa.get(id);
    if(father == id) {
        return id;
    } else {
        return find(father);
    }
}

由于采用了上面这种方法后，对节点的父节点的指向并没有做出改变，仅仅是用其中一个直接指向另一个的father而已，所以如果测试数据比较***，构建的树的深度就会很大，从而遍历的深度增加，就会很慢。

所以我思考了之后，决定要采用路径压缩的方法，代码就变成了下面这样：

public int find(int id) {
 	if(fa.get(id) != id) {
        fa.put(id, find(fa.get(id)));
    }   
    return fa.get(id);
}

采用以上这个方法，把所有的节点都指向根节点了，按理说会减少递归次数，性能应该会增强才对，但是在bug修复时却发现这样的性能更弱了。

后来跟助教交流过之后，分析的原因是，有可能对map的操作变多了 ，可能是调用fa.get(id)的次数过多，第一个方法里是获取了一个fa.get(id)然后存储在father这个局部变量里之后再使用，但是第二个方法最坏的情况下会调用三次，可能是这个地方造成了常数的瓶颈，所以应该试一试把一些东西用局部变量存起来。

也就是如果采用以上的方法，可能会在人多的时候造成栈溢出。

于是我又改成了下面这样，先将find其父节点的返回值保存，再替换和返回：

public int find(int id) {
      if (fa.get(id) == id) {
          return id;
      }
      int ans = find(father.get(id));
      father.put(id, ans);
      return ans;
  }

hw10

UML图

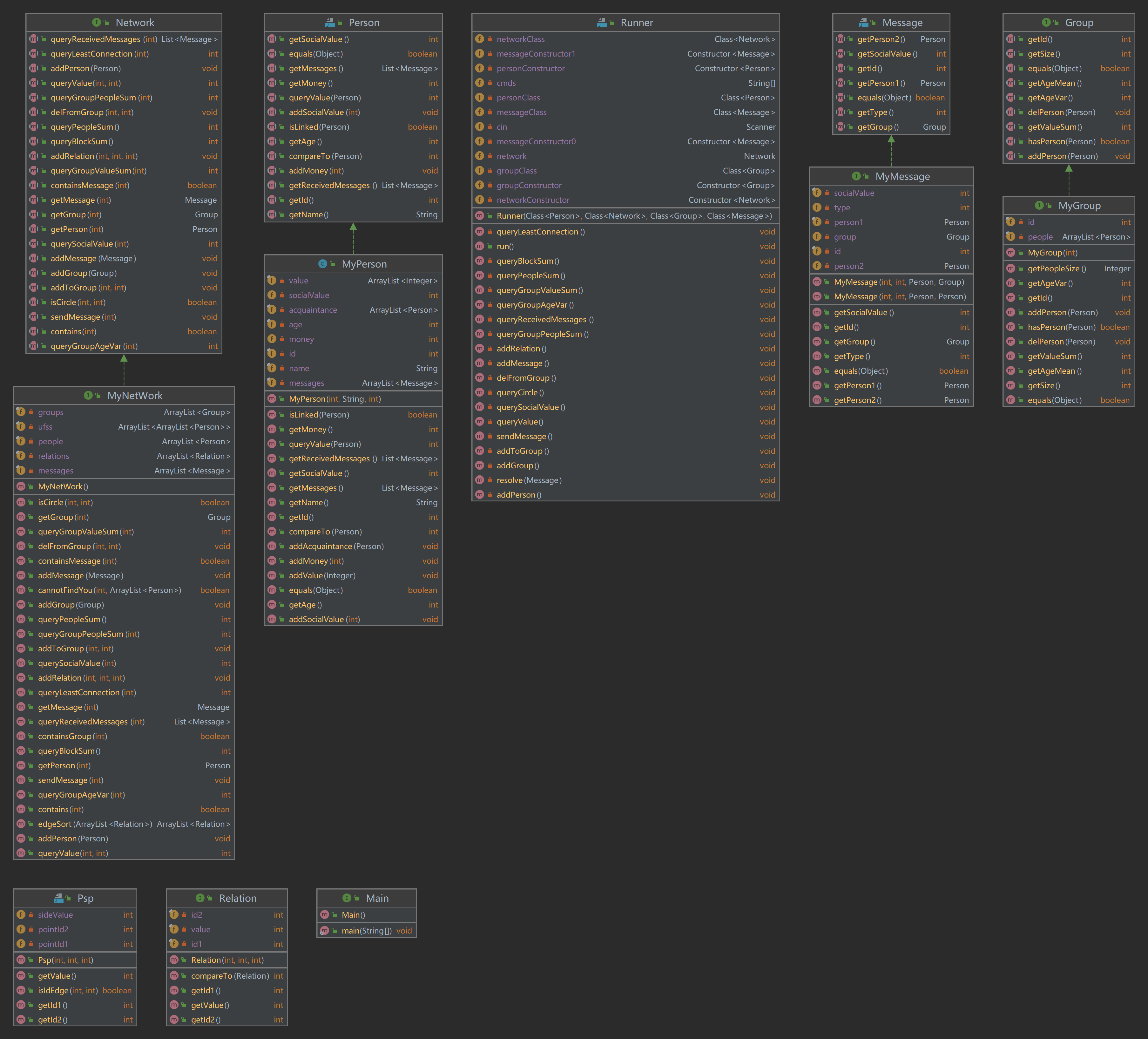
最小生成树——Kruskal算法

针对queryLeastConnection这个方法，要求某点可达的所有点组成的自小生成树。关于最小生成树可选的方法有Prim算法和Kruskal算法，这里我选择的是Kruskal算法，维护了边的序列，实现了判断两个点是否可以连通的方法。

根据图的一个定理，那么如果一个最小连通图有n个点，那么他的最小生成树一定有n-1条边。所以这个算法的主要思路是，首先将所有的边按照他们各自的权重大小进行一个排序，之后从大到小依次选择每条边。如果这条边加入后没有出现回路那么就加入，否则舍弃。这样的话，需要维护几个方法有：

• 判断加入新的一个边之后是否会出现回路——维护并查集，表示与某一点连通的所有点，要求加入的边两端不在同一集合内。
• 按照边的权重排序——维护边序列，在这个序列里边有序排列，可以查找合适位置进行插入。

hw11

UML图

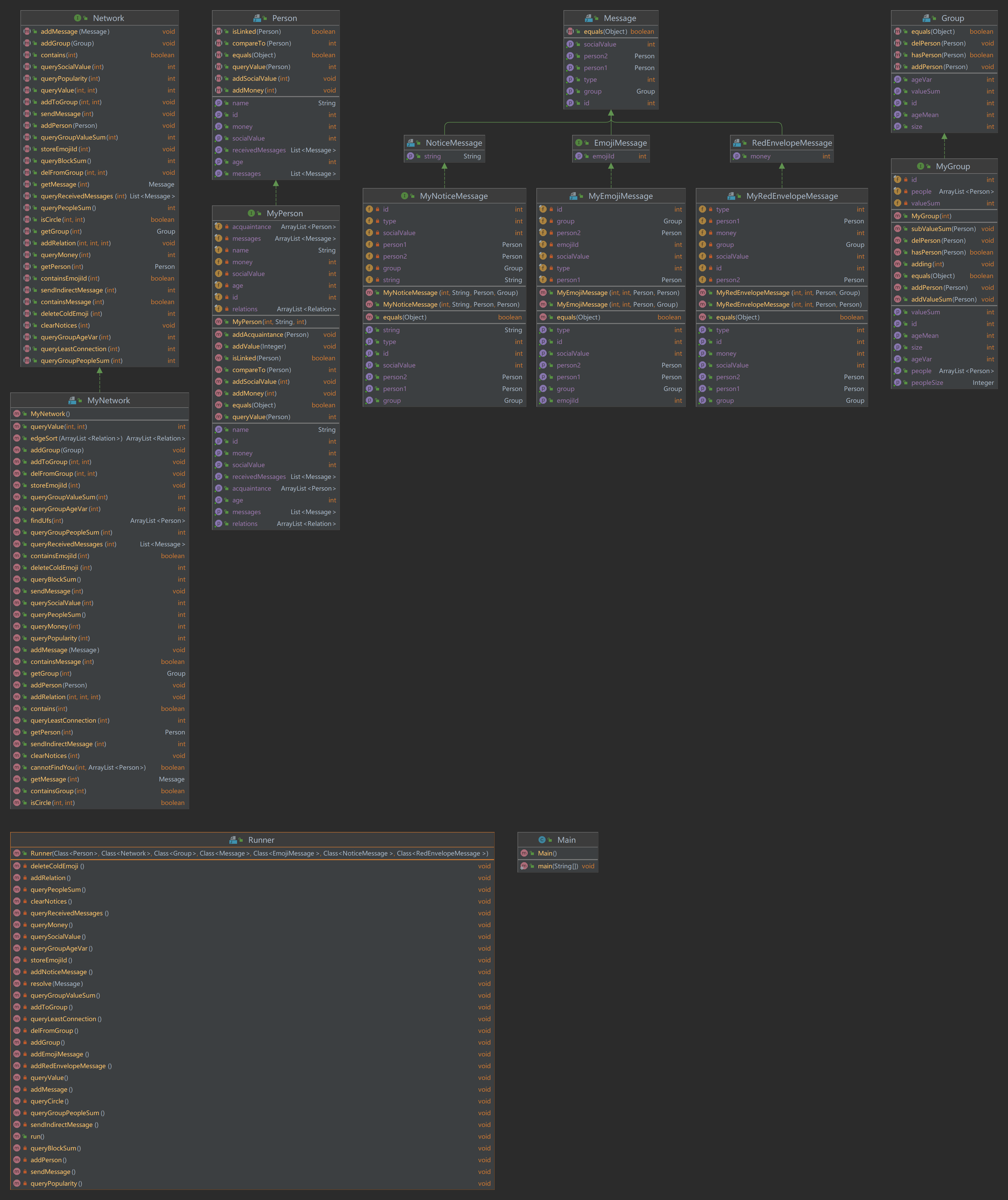
堆优化的Dijistra

这个主要针对的是sendIndirectMessage这个方法，这个方法要求的是两个点之间的最短路径，关于最短路径最经典的方法是Dijistra算法。Dijistra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。

Dijkstra算法采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合T；初始时，原点s的路径权重被赋为0 （dis[s] = 0）。若对于顶点s存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。

初始时，集合T只有顶点s。然后，从dis数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入到T中，此时完成一个顶点，然后，我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值。然后，又从dis中找出最小值，重复上述动作，直到T中包含了图的所有顶点。

二、自测策略与bug分析

Junit测试程序

本单元的指导书中建议用Juint单元测试测试程序，我在测试时也采用了这种方法，Juint的单元测试是利用一个相关插件自动生成测试文件，并且在这个测试文件中针对要测试的方法编写测试方法。具体是在该方法内，新建一个待测试的类，在该测试方法中先创建相关环境，再将测试方法得到的结果返回值同正确结果返回值比较。

JUnit中有两个基本对象：

• TestCase：TestCase可以为测试提供一组方法，在创建测试程序的时候继承TestCase的类，按照需要编写自己的测试方法即可。后来从跟同学交流发现这个可以在IDEA的插件帮助下快速完成，节省了大量的时间在编写测试用例上。
• TestSuite：TestSuite由几个TestCase或者TestSuite组成，使用TestSuite可以创建一个用于测试的树形结构。

但是JUnit的测试需要基于对于JML完全理解的基础上，并且需要提前构造好数据。

比较遗憾的是，由于自己有点偷懒的心态，过了弱测中测之后就不想再自己测试了，所以强测被干的很惨Orz。

第三单元是我提交次数最少的一个单元，因为弱测中测实在太弱了，以至于给我了一种像交设计文档一样只要交上去就对的错觉，但是这种写代码时的轻松真的是有代价的……

对拍

由于本单元不像前两个单元，大家的输出结果在正确的情况下一定是相同的，所以找同学对拍应该是最简单有效的方式。

读代码

因为这一单元有JML的限制，所以大家的代码结构都不会相差很大，有时直接阅读代码也是很好的debug和互测策略。

Bug分析

我在强测和互测中出现的bug全都是tle引起的，由于一开始没有采用并查集的算法而是使用ArrayList实现存储，在第一次作业的时候性能还是不错的，到第二次和第三次作业的时候，劣势就显现出来了，所以我后来改变了原有的写法，采用了助教提供的并查集方法。在第三次作业的bug修复时，我采用了堆优化来提高性能。

三、扩展任务

假设出现了几种不同的Person

• Advertiser：持续向外发送产品广告
• Producer：产品生产商，通过Advertiser来销售产品
• Customer：消费者，会关注广告并选择和自己偏好匹配的产品来购买 -- 所谓购买，就是直接通过Advertiser给相应Producer发一个购买消息
• Person：吃瓜群众，不发广告，不买东西，不卖东西

如此Network可以支持市场营销，并能查询某种商品的销售额和销售路径等 请讨论如何对Network扩展，给出相关接口方法，并选择3个核心业务功能的接口方法撰写JML规格（借鉴所总结的JML规格模式）

相关接口方法

前三种person均可以继承Person类，同时增加Product类，表示商品，每个product都有自己的id，并且advertiser有一定数量的product缓存。

JML规格撰写

setPreference

  /*@ public normal_behavior
    @ requires (\exists int i; 0 <= i && i < people.length;
    @          (Personid == people[i].getId()) && (people[i] instanceof Customer)) 
    @          && (\exists int i; 0 <= i && i<= products.length;
    @          products[i].getId() == ProductId);
    @ assignable getPerson(personId).preferences;
    @ ensures getPerson(personId).prefer(ProductId);
    @ ensures (\forall Product i;\old(getPerson(PersonId).prefer(i)); 
    @         getPerson(PersonId).prefer(i));
    @ public exceptional_behavior
    @ signals (PersonIdNotFoundException e) !(\exists int i; 
    @         0 <= i && i < people.length;people[i].getId() == id && 
    @         people[i] instanceof Customer);
    @ signals (ProductIdNotFoundException e) !(\exists int i; 
    @          0 <= i && i < products.length;products[i].getId() == ProductId);
    @ */
    public void setPreference(int PersonId, int ProductId) throw PersonIdNotFoundException, ProductIdNotFoundException;

produce

  /*@ public normal_behavior
      @ requires (contains(id1) && (getPerson(id1) instanceof Producer));
      @ requires getPerson(id1).containsProduct(id2);
 	  @ ensures (getPerson(id1).getProduct(id2).amount =
      @         \old(getPerson(id1).getProduct(id2).amount) + 1);
	  @ ensures (getPerson(id1).productList.length ==
      @         \old(getPerson(id1).productList.length));
      @ public normal_behavior    
      @ requires (contains(id1) && (getPerson(id1) instanceof Producer));
      @ requires !getPerson(id1).containsProduct(id2);
      @ ensures getPerson(id1).getProduct(id2).amount = 1;
      @ ensures (getPerson(id1).productList.length ==
      @         (\old(getPerson(id1).productList.length) + 1));
      @*/
    public void produce(int id1, int id2);

purchase

    /*@ public normal_behavior
      @ requires containsProduct(productId);
      @ requires getPerson(id2).getProduct(productId).amount > 0;
	  @ requires contains(id1) && (getPerson(id1) instanceof Customer);
      @ requires contains(id2) && (getPerson(id2) instanceof Producer);
      @ ensures getPerson(id1).money = 
      @         (\old(getPerson(id1).money) - getProduct(productId).getValue);
      @ ensures getPerson(id2).money = 
      @         (\old(getPerson(id2).money) + getProduct(productId).getValue);
      @ ensures getPerson(id2).getProduct(productId).amount =
      @         (\old(getPerson(id2).getProduct(productId).amount) - 1);
      @*/
    public void purchase(int id1, int id2, int productId);

四、学习体会

这一单元的难度明显比前两个单元小了很多，重点考察的也是和图相关的一系列算法，与之前作业不同的是，将自然语言描述换为了JML规格描述，在理解了JML规格之后，重点也就似乎回到了数据结构的相关知识上。

JML语言最大的优势应该就是表述清晰，不会出现歧义，因此这次的作业只要按照JML严格执行，就不会出现除了TLE之外的错误，但是JML语言理解起来确实比较困难，尤其是涉及到比较复杂的函数，就会出现多层括号嵌套的JML规格，读起来确实有点头疼。在实验和研讨课里也写过JML规格，写JML也是难度不小的一件事，因为要充分考虑各种可能出现的情况，并且要用JML正确表达想法，不然一旦JML出错，就会造成很大的问题。

总体来说这一单元难度还是小的，但是其实学完了之后感觉收获不是很大。相比上一个电梯单元的各种阴间错误，这一单元是代码量太大以至于给我感觉是有点重复劳动了，有点付出和收获不成正比的感觉。尤其checkstyle限制文件总行数不能超过500行，但是要实现的方法确实很多，为了代码风格拿高分，我在减少行数的过程中，做出了许多违背自己最初想法的改动，牺牲了代码的可读性来满足代码风格，我觉得有点本末倒置了。

JML毕竟只是一种规格语言，是否精通JML似乎没有那么重要，我觉得更重要的是通过这次作业，要掌握基于规格实现代码的思想，以及掌握代码写作规范。