BUAA_OO_第一单元总结
第一单元作业进行的是表达式的去括号与化简。
第一次作业要求对表达式的结构进行建模,完成单变量多项式的括号展开;第二次作业在第一次作业的基础上增加了单层括号嵌套的三角函数、自定义函数与求和函数;第三次作业将第二次作业的功能进一步扩展,要求完成多层嵌套的表达式和函数调用的括号展开与化简。
思路
第一次作业
由于本人能力有限,加上第一周时间较为紧张,所以第一次作业采用了题中所给的预解析的方法,思路较为简单。
-
设立一个表达式类与一个主类,并建立表达式容器,采用预解析每次读入一个新fn后,用表达式容器中具体的表达式替换相应参与运算的符号fn,继而创建一个新的表达式对象并将其存入表达式类;
-
在对表达式进行处理时,采用
switchcase结构,对各运算add、sub、mul、pow、pos、neg以及常量数字分别进行较为简单的处理; -
在所有多项式都处理完之后,对最终形成的不含括号的表达式进行进一步化简,因为担心出错,所以只进行了类似
--x+-x这种赘余符号的处理和0项比如x**0x*0的处理,而并未进行合并同类项,至此,第一次作业的构建基本完成。
第一次作业我基本延续了C语言的写法,没有体现面向对象的思维方法,总体来说不值得提倡。但在构建代码过程中,我也采用了一些较为巧妙的策略使得利用相对较少的代码量便完成了第一次作业。
在我的构建中,空格是关键,由于采用预解析读入时表达式是不含有多余空格的,但是空格又是我用于区分不同项的关键,所以我在每一部分运算的处理时,会有选择地在必要之处添加空格。具体是,只在项之前加空格,对于+ - 号,若其表示的是neg、pos的含义,则将其和其后的内容看作一个整体,不在其前加空格;若其表示的是add、sub的含义,则在其前添加空格,处理好后存入表达式容器中,后续会利用split()函数根据空格存在的位置将各个项分割并存入数组,以便于表达式mul 和 pow 计算,以保证结果正确性。
第二次作业
第二次作业若仍沿用预解析,则方法很简单,只需要添加cos sin 的case,并对其进行相应处理即可,总体添加的代码量在十行以内,但使用预解析是第一次作业时间实在不够的无奈之举,第二次时间相对充足 ,所以便思考如何实现预解析的过程。
解决的方法也很简单,可以使用栈的方法,读入所求表达式,并将读入的中缀表达式转为后缀表达式,之后出栈进行计算,构建各种运算add 、sub、mul、pow、pos、neg、sin、cos的类,并在主体上依旧延续第一次作业的整体架构,便完成了第二次作业的处理。
第三次作业
第三次作业增加的内容并不多,仅在第二次作业的基础上完成了一些扩展功能,实现了可以多层嵌套的三角函数和自定义函数。但是由于架构问题,我的第二次作业并不能轻易的实现第三次作业的要求,若在每个运算的类中实现增量,那么在输出结果中则会出现各种新的和旧的bug,甚至之前已通过的测试点也会出错。
原因在于,若在程序最后统一处理,一般情况没有什么大问题,但是若有cos这种情况出现时,便会出错,因为cos实际上起的是一个去符号,或者称为加绝对值的作用,但是在原来的架构中,我把cos视为和()一样的效果,忽略了这种特殊情况,也导致了第二次作业收到hack。
仔细考虑后,我决定修改自己的架构,将原来的化简过程和去除赘余符号的步骤由原来的放在代码最后统一处理改为在每一项分别处理,由于表达式的处理实际上是由因子—>项—>表达式过程,而表达式又可作为表达式因子,所以又可将其带入因子的部分从而重现因子—>项—>表达式的过程,实际上是一个递归的思想,借助这一思想,那么其实我的处理就简单了很多,只对每一步处理,处理时只考虑最简单情况即可,因为参与处理的项或因子或表达式,都是在前几部中已经经过化简的,借此便也完成了第三次作业的编写。
综合
三次作业之后,目前的作业整体架构是:
读入表达式 —> 对表达式进行预处理 —> 解析表达式 —> 化简表达式
程序结构分析
因为使用了预解析加上程序结构比较差,面向对象的思维基本没有体现,所以UML图和复杂度度量都极为单薄…
第一次作业UML图
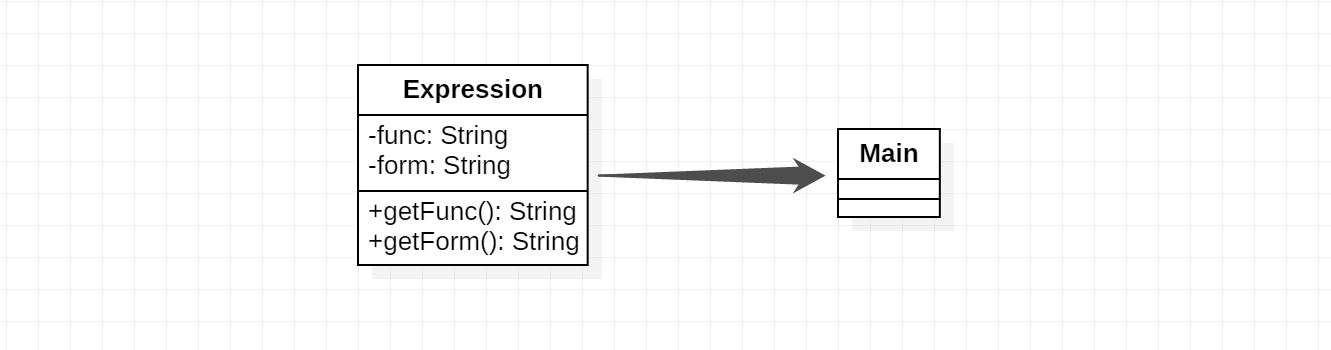
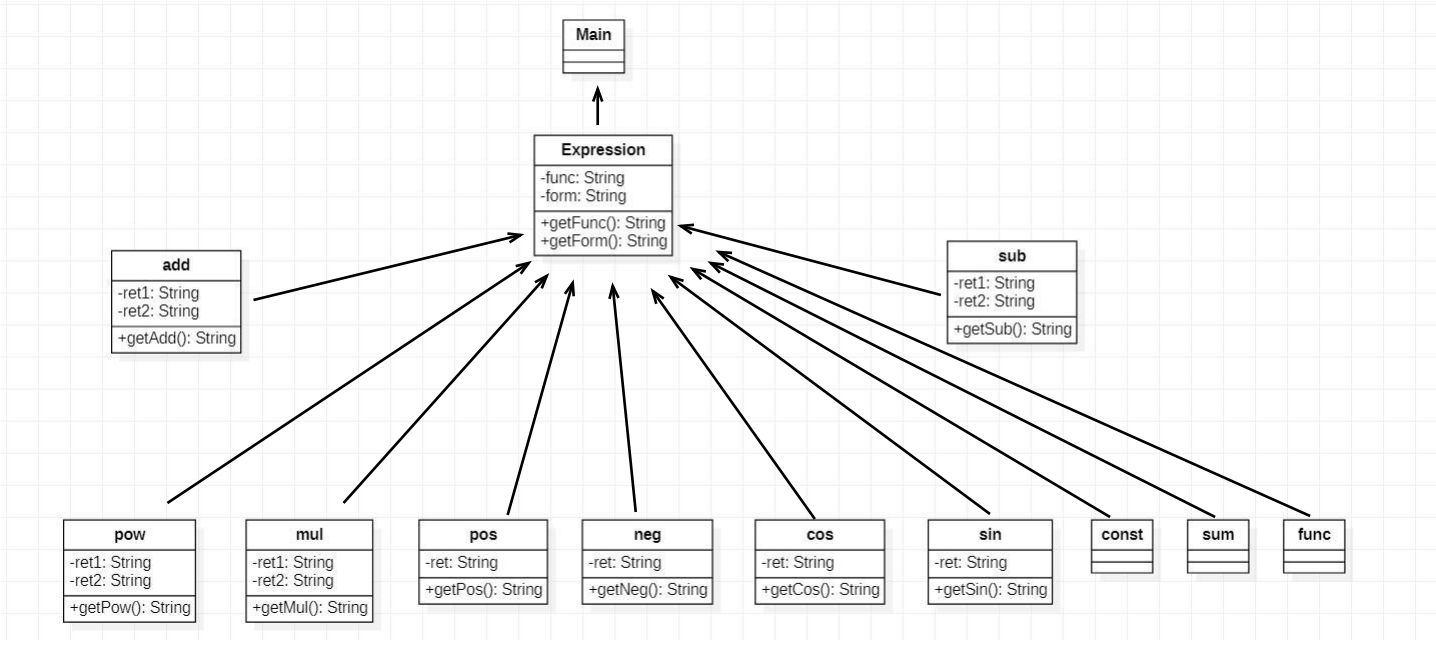
第二三次作业UML图
度量
-
CogC 认知复杂度
-
ev(G) 基本复杂度
-
iv(G) 模块设计复杂度
是用来衡量模块判定结构,即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度,因此模块设计复杂度不能大于圈复杂度,通常是远小于圈复杂度。
-
v(G) 圈复杂度
是用来衡量一个模块判定结构的复杂程度,数量上表现为独立路径的条数,即合理的预防错误所需测试的最少路径条数,圈复杂度大说明程序代码可能质量低且难于测试和维护,经验表明,程序的可能错误和高的圈复杂度有着很大关系。
第一次作业复杂度
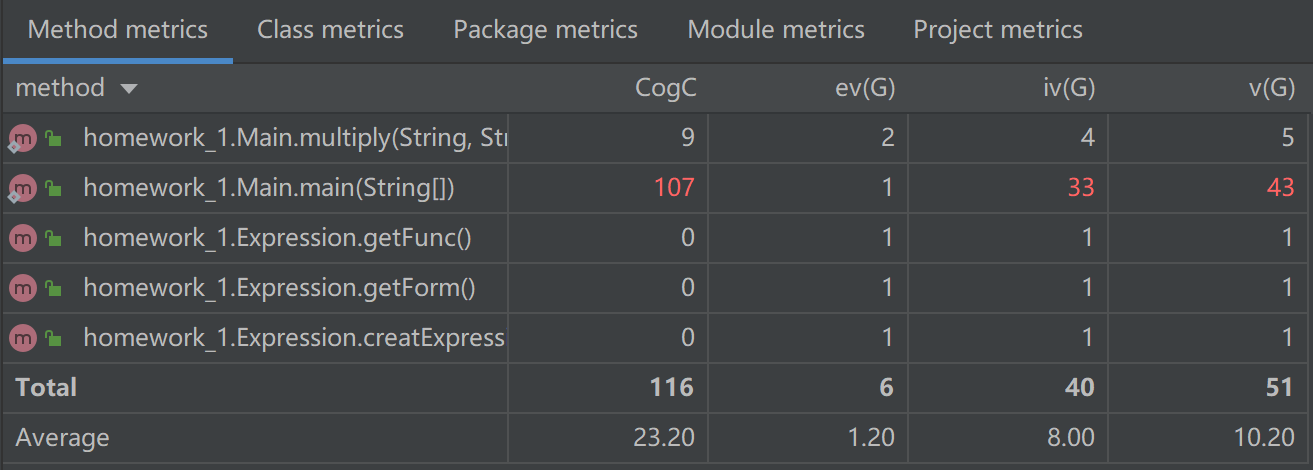
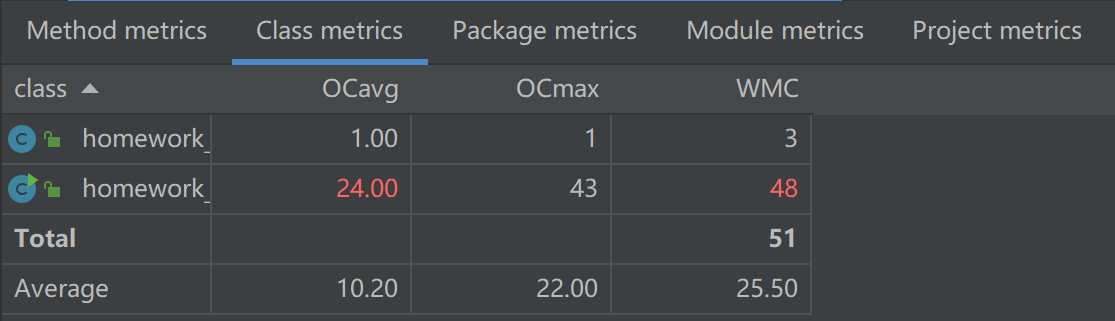
第二次作业复杂度
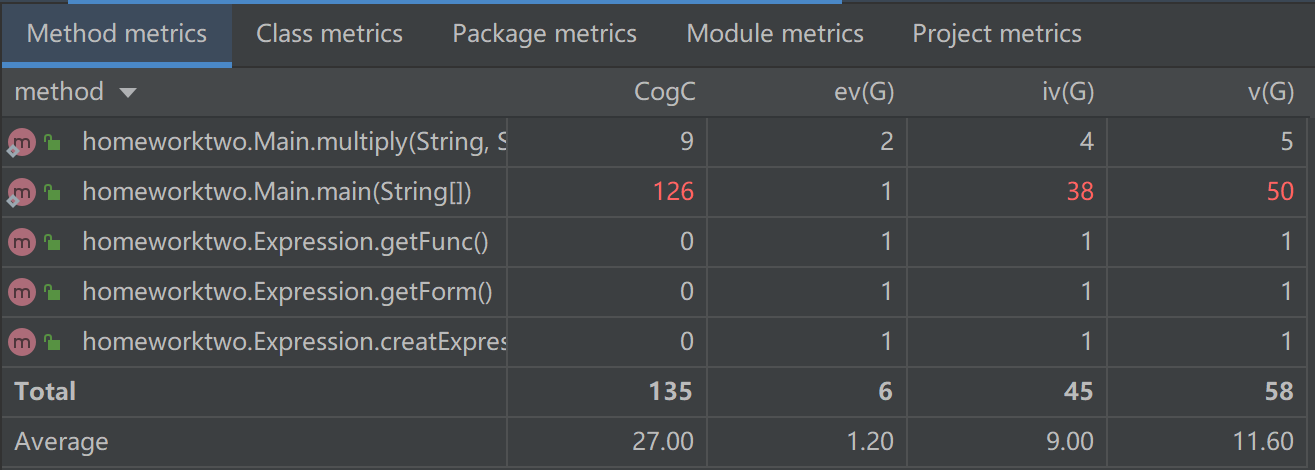
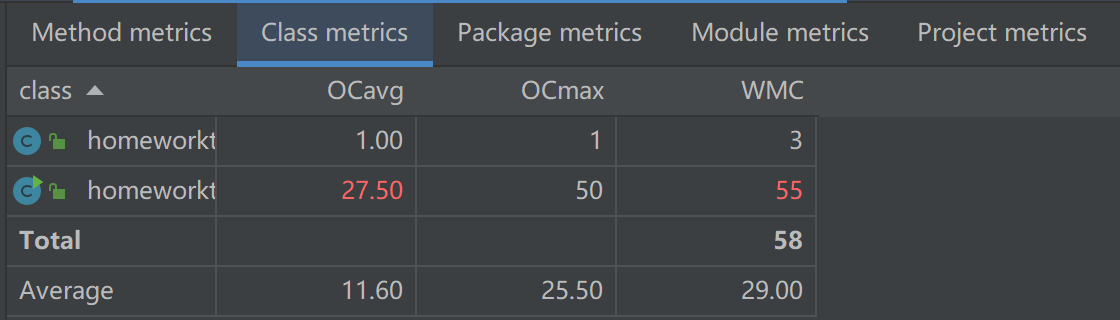
第三次作业复杂度
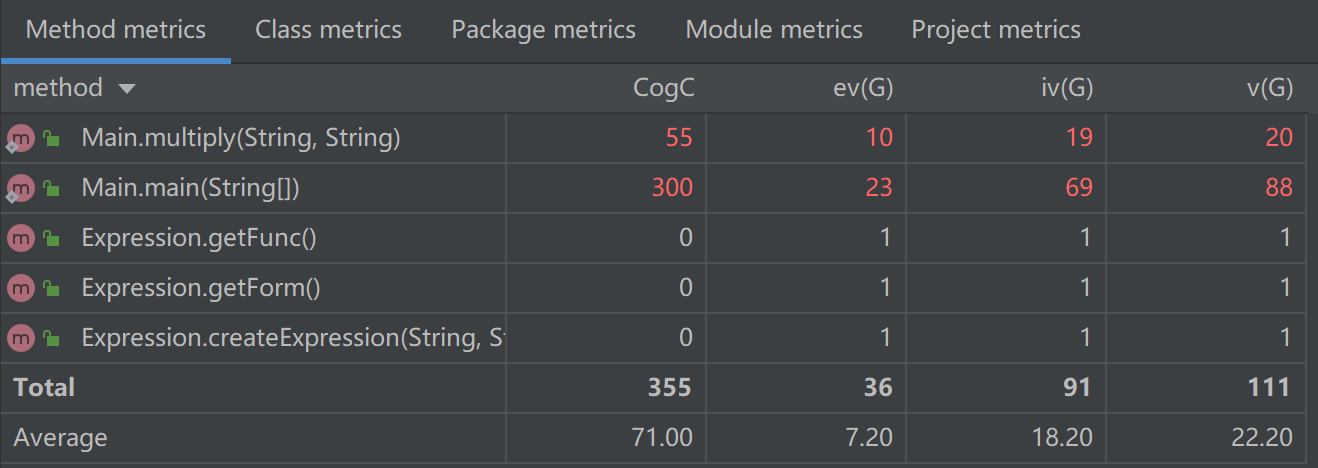
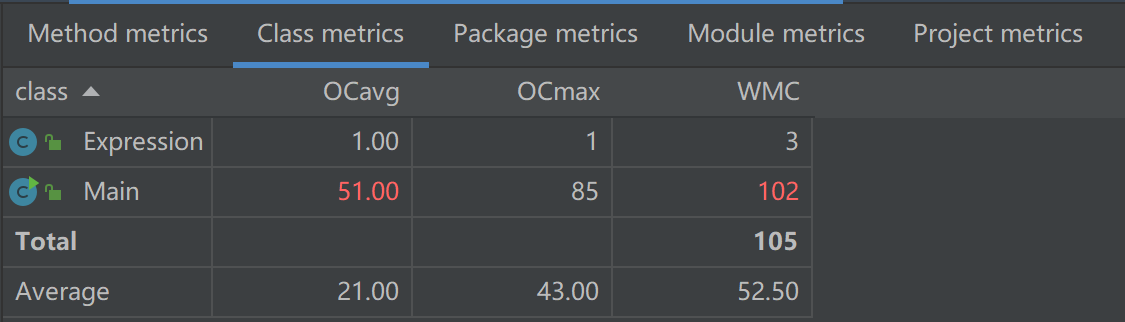
三次作业bug分析
第一次作业
第一次作业的架构还较粗糙,bug也相对较致命,由于第一次作业时思路仍不太清晰,导致去符号出错,具体出错的点在,比如,输入(x+ x+ x) - (x+ x) *x * x ** 0时,我的输出为x+x+x+x*x*1x*x*1,很明显可以看出出错在于1和x之间的符号被吞了,经过一系列debug之后,我找到了问题所在,主要是由于对空格的使用不当,已经没有区分+、-作为运算符和作为正负号的区别,导致项的划分不清楚以至的出错。这一点也在后续的hack中被不断攻击,十分惨烈。
第二次作业
经过第一次作业的强测和互测,第二次作业关于第一次作业中几种运算的表达式问题没有再出bug,而第二次的bug主要在于新增的三角函数符号的处理,对于cos()函数,由于盲目的想优化删去符号以至于忽略了cos()函数内部恒正的性质,以至于输入cos(-1)时,竟输出了-cos(1)的情况,在hack阶段被找到bug后也对此进行了修改,不过竟然侥幸过了强测。
第三次作业
相比起前两次作业受到的hack,第三次作业的hack显得尤为蠢。原因在于导入了官方的official(3)的包之后,竟然忘记修改头文件,头文件仍然是official(2)的头文件,在hack阶段由于版本问题出现了format error而被hack,虽然过了强测但是互测还是死得很惨。
不过第三次作业最痛苦的debug是在过弱测和中测的时候,由于我在第三次作业对架构进行了重新搭建,以至于出现了很多在一二次作业中的bug,输入x*cos((x+x))却输出了x*cos((x))+x*cos((x))的结果,这是由于空格使用的不当导致了错误的项的分割,于是为了解决空格问题,我将所有存入表达式容器的内容中的空格删去,并在每一步单独处理并化简,最终完成了第三次作业。
hack策略
-
评论区看到很多人分享自己的自动化测试程序,但是利用自动化程序生成数据时,对于程序的要求较高,我自己写过较简单的自动化生成程序,但是效果比较差,由于数据输入的限制较多,加上程序功能比较简单,因此生成的数据较弱,且很容易就出现数据不合法的情况,所以最终没有采取这种方式。
-
尝试边界数据,测定数据类型是否合理,尝试多层函数嵌套。
-
集中关注复杂度较高的环节,如输入部分、三角函数部分等。
-
关注化简的较多的代码,因为一般bug都是出在优化阶段。
-
还有一点就是利用自己的错误点,会把自己在debug自己的程序时遇到的比较***钻的数据保存下来,在互测阶段测试别人。
心得体会
这次作业比较遗憾的是采用了预解析和面向过程的解题方法,这也导致自己的UML类图和度量分析显得比较捉襟见肘,几乎没什么内容。其实还是因为第一周在面对一门几乎全新的语言时比较怯,所以更倾向于选择自己熟悉的解题思路,不管是预解析还是栈,都是已经比较熟悉的内容,所以有点临阵脱逃的意味,这也导致第一次oo研讨课时我个人的体验感比较差,参与度也比较低。总而言之,作为6系人,更多时候应该相信自己,直面挑战。
这三次作业也让我体会到了架构的重要性,由于前两次架构的不合理,才导致了第三次作业的大规模更改,除此之外,在本单元作业中,我的层次化的设计并没有充分的体现,结构还相对比较混乱,三次作业过后,我还是不能交出一份很让自己满意的代码,在以后的设计中,要充分考虑代码的可扩展性,要有高瞻远瞩的思考。
关于hack,第一次参加hack的时候,因为不太懂寻找方法因此盲目的hack了几个小时但是没有收获,所以第二周的时候对hack的热情有所减少。但是后来发现,hack时通过观看别人的代码,也可以学习到他人的一些巧妙设计,借鉴别人的优点;除此之外,找别人的bug过程,不但锻炼了自己构造数据的能力,也增加了自己对题目理解的深度,使自己考虑问题更全面。只要用心,也能收获很多。
第一单元告一段落,不管结果是否满意,但是不得不承认在这期间我确实学到了很多,在今后的学习中,希望自己可以及时总结和反思,不断吸取经验教训。



