1136. 平行课程(拓扑排序)

1136. 平行课程

已知有 N 门课程，它们以 1 到 N 进行编号。

给你一份课程关系表 relations[i] = [X, Y]，用以表示课程 X 和课程 Y 之间的先修关系：课程 X 必须在课程 Y 之前修完。

假设在一个学期里，你可以学习任何数量的课程，但前提是你已经学习了将要学习的这些课程的所有先修课程。

请你返回学完全部课程所需的最少学期数。

如果没有办法做到学完全部这些课程的话，就返回 -1。

 

示例 1：

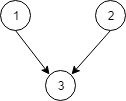
输入：N = 3, relations = [[1,3],[2,3]]
输出：2
解释：
在第一个学期学习课程 1 和 2，在第二个学期学习课程 3。

示例 2：

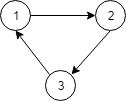
输入：N = 3, relations = [[1,2],[2,3],[3,1]]
输出：-1
解释：
没有课程可以学习，因为它们相互依赖。

 

提示：

1. 1 <= N <= 5000
2. 1 <= relations.length <= 5000
3. relations[i][0] != relations[i][1]
4. 输入中没有重复的关系

class Solution {
public:
    int minimumSemesters(int n, vector<vector<int>>& relations) {
        vector<unordered_set<int>> graph(n + 1); // 用邻接表存储节点与边的关系
        vector<int> indegree(n + 1); // 存储顶点的入度
        // 构建课程与先修关系图
        // X->Y, 学习Y课程必须先学习X课程
        for (auto &vec : relations) {
            indegree[vec[1]]++;
            graph[vec[0]].insert(vec[1]);
        }
        queue<int> q; // 存储入度为0的课程
        for (int i = 1; i <= n; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }
        int step = 0; // 学完全部课程所需的最少学期数
        int cnt = 0; // 学习课程数
        // BFS进行逐层剪枝选修课程
        while (!q.empty()) {
            int size = q.size();
            step++;
            for (int i = 0; i < size; i++) {
                int temp = q.front();
                q.pop();
                cnt++;
                // 剪枝去除边,相当于对端顶点的入度--,如果剪枝后对端顶点的入度为0则入队
                for (auto node : graph[temp]) {
                    indegree[node]--;
                    if (indegree[node] == 0) {
                        q.push(node);
                    }
                }
            }
        }
        return (cnt < n) ? -1 : step;
    }
};