24.12.23

菜死了啊啊啊

A

luogu P9266

耶？这不是我们决策单调性嘛，我能受这委屈，我刚学的擒拿术。
然后靠着渺远的记忆加了 wqs 二分。
然后冲了一整场爆蛋了。
🤡👈🤣

首先需要知道怎么快速求区间权值。

我们考虑最优的决策点一定是 \(s_i = (\) 且 \(s_{i + 1} = )\) 的，不然移到最近的这种位置一定使划分的两个区间权值不增。

如果划分的次数 \(k - 1\) 比决策点多答案为 \(0\)。

考虑合法括号序列的包含关系构成一棵树，一个节点包裹范围内的总权值是 \(\sum_{y \in ch_x} val_x + \binom{|ch_x|}{2}\)。
为方便处理，给每段极长合法子段建立虚根，其范围的权值计算方式同上。

那么由于上面对最优决策点的讨论所以划分的位置一定在叶子上。
对于一个划分出来的区间从两端点的叶子可以求出 LCA。
那么贡献区域应该长成这样：

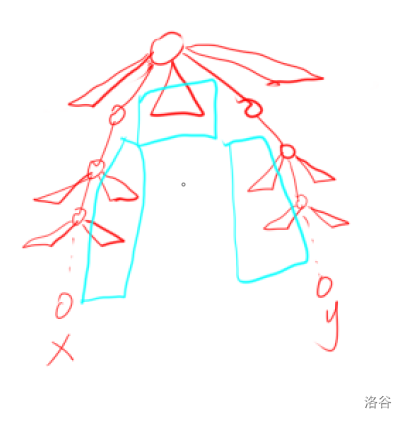
三角形是省略了的子树。

对于链上的右翼和左翼显然可以树上前缀和计算，
对于 LCA 子节点中间部分可以维护前缀和快速求区间和以及个数（用上面那个式子）。

所以上面需要求 LCA 和一个点在某个点方向的直接儿子（树上 k 级祖先）。
所以这里其实是可以预处理单次 \(O(1)\) 求的，但是重剖学傻 er 直接上 \(O(\log)\) 了。

哦还有特殊情况是两个划分点不属于同一极长合法子段。

这个直接树上前缀和求两个翼的权值和，中间的虚根们求区间和（注意不算组合数）。

如果需要计算没有左端点或右端点的区间代价额外处理一下。

Code with prework

int build(int l, int r, int bl) {
		int x = ++idx; id[l] = id[r] = x;
		val[x] = 1; bel[x] = bl;
		rep(i, l + 1, r - 1) {
			assert(s[i] == '(' && mch[i]);
			ch[x].push_back(build(i, mch[i], bl));
			val[x] += val[ch[x].back()];
			i = mch[i];
		}
		if (ch[x].size()) {
			sum[ch[x][0]] = val[ch[x][0]]; cnt[ch[x][0]] = 1;
			rep(i, 1, ch[x].size() - 1)
				sum[ch[x][i]] = sum[ch[x][i - 1]] + val[ch[x][i]],
				cnt[ch[x][i]] = cnt[ch[x][i - 1]] + 1;
			val[x] += C2(ch[x].size());
		}
		return x;
	}

	LL Lsum[N], Rsum[N];
	void dfs(int x) {
		for (int y : ch[x]) {
			Lsum[y] = Lsum[x] + sum[y] - val[y] + C2(cnt[y] - 1);
			Rsum[y] = Rsum[x] + sum[ch[x].back()] - sum[y] + C2(cnt[ch[x].back()] - cnt[y]);
			dfs(y);
		}
	}

	int son[N], siz[N], top[N], dfn[N], rnk[N], dcnt;
	void dfs1(int x) {
		siz[x] = 1;
		for (int y : ch[x]) {
			fa[y] = x; dep[y] = dep[x] + 1; 
			dfs1(y); siz[x] += siz[y];
			if (siz[y] > siz[son[x]]) son[x] = y;
		}
	}
	void dfs2(int x, int tp) {
		top[x] = tp; dfn[x] = ++dcnt; rnk[dcnt] = x;
		if (son[x]) dfs2(son[x], tp);
		for (int y : ch[x]) if (y != son[x]) dfs2(y, y);
	}
	int Lca(int x, int y) {
		while (top[x] != top[y])
			dep[top[x]] > dep[top[y]] ? x = fa[top[x]] : y = fa[top[y]];
		return dep[x] < dep[y] ? x : y;
	}
	int kfa(int x, int k) {
		while (dep[x] - dep[fa[top[x]]] <= k)
			k -= dep[x] - dep[fa[top[x]]], x = fa[top[x]];
		return rnk[dfn[x] - k];
	}
	int Son(int x, int y) {
		if (x == y) return y;
		return kfa(y, dep[y] - dep[x] - 1);
	}

	LL W(int l, int r) {
		if (l == 1 && r == n) return sum[Rt.back()];
		if (l == 1) {
			int y = id[r];
			LL res = sum[bel[y]] - val[bel[y]];
			res += Lsum[y];
			return res;
		}
		if (r == n) {
			int x = id[l];
			LL res = sum[Rt.back()] - sum[bel[x]];
			res += Rsum[x];
			return res;
		}
		int x = id[l], y = id[r];
		if (bel[x] != bel[y]) {
			LL res = sum[bel[y]] - val[bel[y]] - sum[bel[x]];
			res += Lsum[y] + Rsum[x];
			return res;
		} else {
			int lca = Lca(x, y), fx = Son(lca, x), fy = Son(lca, y);
			LL res = sum[fy] - val[fy] - sum[fx] + C2(cnt[fy] - 1 - cnt[fx]);
			res += Lsum[y] - Lsum[fy] + Rsum[x] - Rsum[fx];
			return res;
		}
	}

	void prework() {
		bool fl = 0;
		rep(i, 1, n) {
			if (mch[i]) {
				if (!fl) Rt.push_back(++idx), fl = 1;
				ch[Rt.back()].push_back(build(i, mch[i], Rt.back()));
				i = mch[i];
			} else fl = 0;
		}
		rep(i, 0, Rt.size() - 1) {
			int x = Rt[i];
			for (int y : ch[x]) val[x] += val[y];
			val[x] += C2(ch[x].size());
			sum[x] = val[x];
			if (i) sum[x] += sum[Rt[i - 1]];
			sum[ch[x][0]] = val[ch[x][0]]; cnt[ch[x][0]] = 1;
			rep(i, 1, ch[x].size() - 1)
				sum[ch[x][i]] = sum[ch[x][i - 1]] + val[ch[x][i]],
				cnt[ch[x][i]] = cnt[ch[x][i - 1]] + 1;
			dfs(x); dfs1(x); dfs2(x, x);
		}
	}

我知道我写的很屎。

然后已经会 \(O(\log n)\)（或 \(O(1)\)）求区间权值了。

然后就是 wqs 二分套决策单调性了。

就是二分一个区间的额外权值，跑决策单调性 dp，同时记录决策划分的段数。
根据 dp 出最优的答案的段数调整额外权值。
最后把最终的额外权值带进去跑一遍，最后的答案减去区间数乘上额外权值。

常数相关

ooo，是不是第一次我博客里见三级标题）

之前我使用的板子是

for (int i = 1; i <= n; ++i) {
	while (hed < tal && get(q[hed], q[hed + 1]) <= i) ++hed;
	f[i] = Calc(q[hed], i);
	while (hed < tal && get(q[tal - 1], q[tal]) >= get(q[tal], i)) --tal;
	q[++tal] = i;
}

在队列里只记录了一个值，缺点是每次一询问边界就要二分，导致常数巨大。
所以大家喜欢维护（决策点，左边界）二元组不是没道理的。

rep(i, 1, n) {
	while (hed < tal && _l[q[hed + 1]] <= i) ++hed;
	f[i] = Calc(q[hed], i);
	while (hed < tal && (_l[q[tal]] == n + 1 || Calc(q[tal], _l[q[tal]]) >= Calc(i, _l[q[tal]]))) --tal;
	q[++tal] = i; _l[i] = get(q[tal - 1], i);
}

这个给我减了快一半的常熟。

然后在 wps 二分时上界设成答案最大值（\(W(1, n)\)），多少有点用。

B

NT 贪心模拟网络流秒了/bx/bx/bx。

不如去看 NT 博客

C

luogu P11303

PC ✌教我李超树斜率优化。

P6246

emmm...

首先我们知道一个区间中点以左去左边，中点以右去右边

可以预处理 \(a_1 \sim a_n\) 之间每个位置作为中点，它左边的点要去左边，右边的点要去右边，他左边的第一个点编号是多少。

然后就可以 \(O(1)\) 算区间权值了。

// sum 是 pos 的前缀和
LL Calc(int j, int i) {
	if (j == 0) return pos[i] * i - sum[i];
	int p = pre[pos[j] + pos[i] >> 1];
	LL res = pos[i] * (i - p) - (sum[i] - sum[p]) +
		(sum[p] - sum[j - 1]) - pos[j] * (p - j + 1);
	return f[j] + res - Delta;
} 

然后是和 A 同样的 wqs 二分套决策单调性 dp

void solve() {
	ans = 1e16; ansk = 0;
	q[hed = tal = 0] = 0;
	rep(i, 1, n) {
		while (hed < tal && _l[q[hed + 1]] <= i) ++hed;
		f[i] = Calc(q[hed], i); g[i] = g[q[hed]] + 1;
		LL val = f[i] + (sum[n] - sum[i - 1]) - pos[i] * (n - i + 1) - Delta;
		if (val < ans) ans = val, ansk = g[i];
		while (hed < tal && (_l[q[tal]] == n + 1 || Calc(q[tal], _l[q[tal]]) >= Calc(i, _l[q[tal]]))) --tal;
		q[++tal] = i; _l[i] = get(q[tal - 1], i);
	}
	// LOOK_TIME;
}
// ...
LL l = -1e9, r = -1, res = 0;
while (l <= r) {
	LL mid = l + r >> 1;
	Delta = mid; solve();
	if (ansk >= m) res = mid, r = mid - 1;
	else l = mid + 1;
}
Delta = res; solve();
printf("%lld\n", ans + Delta * m);