蒙皮动画技术（Skinned Animation）

蒙皮动画（Skinned Animation）

过程概述

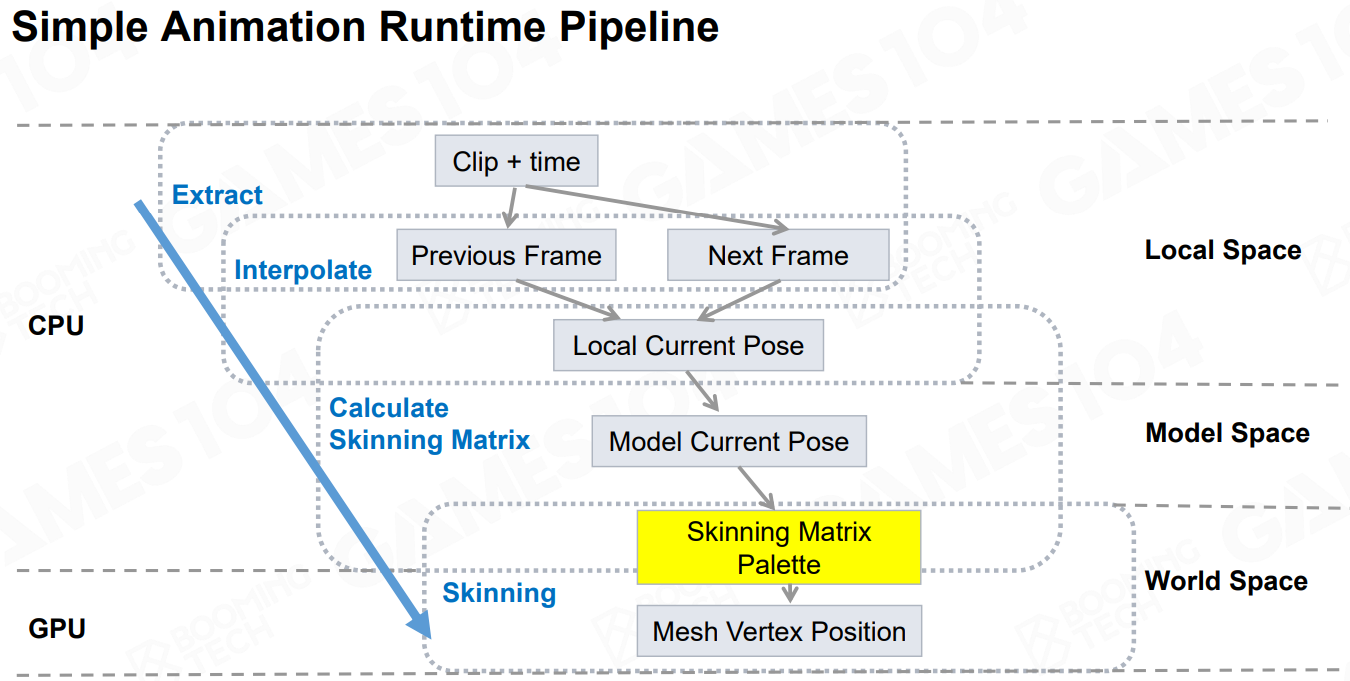
DCC 过程：

创建一个 binding pose 的 mesh
创建一个 binding pose 的 skeleton
对 Mesh 每个顶点进行设置，设置其受各 joint 影响的权重

CPU（每帧）：

解压动画 Clip，并通过 time 访问到相邻两个关键帧 pose
对两个关键帧 pose 进行插值计算得到当前帧的 local space pose，然后再转换成 model space
传入 Skinning Matrix Palette 到 GPU

GPU（每帧）：

渲染角色 mesh（vertex shader 需根据 Skinning Matrix Palette 变换 vertex）

姿势 (Pose)

pose 是角色的某种静止状态，而艺术家设计出多个关键帧的 pose ，然后通过某种插值算法来产生动作（pose 之间的渐变）。

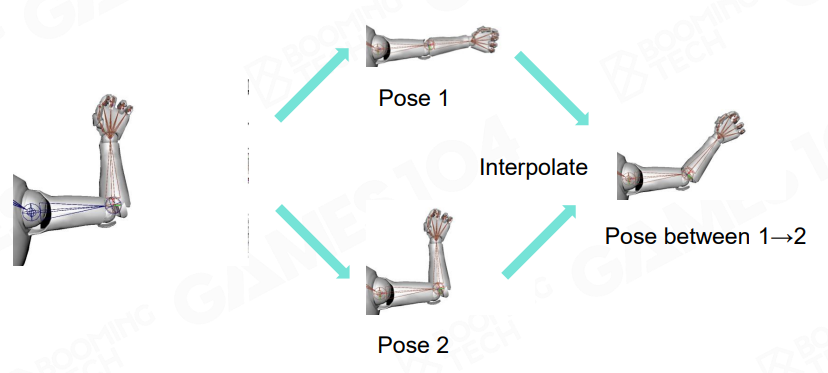
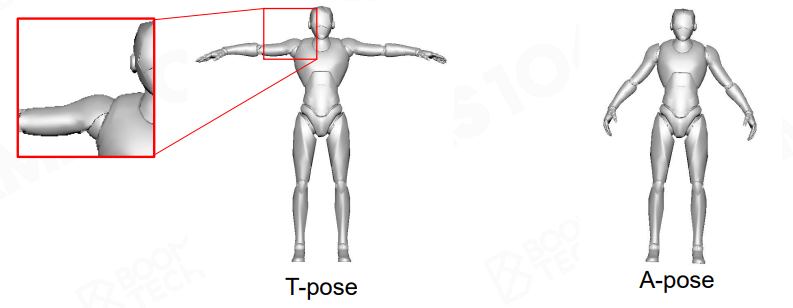
binding pose（绑定姿势）：艺术家进行创作时的初始 pose，往往会让角色呈现出一种比较自然和展开的姿势，以方便创作

主流有两种绑定姿势：T-pose 和 A-pose，业界一般会更倾向于使用 A-pose，这是因为 A-pose 的肩膀会更加自然放松（高精度）而 T-pose 的肩膀容易出现挤压（低精度）

关节 (Joint) & 骨骼 (Bone)

关节 (Joint)：存储关节的旋转、位移、拉伸属性（共 9 DoFs），并且存在父子关节的关系；通过修改关节的属性，来驱动 skeleton 的变化，从而产生角色动画

一般角色拥有 50~100 个 joint；而表示生动的面部表情和加上 gameplay 用途的 joint，则可能超过 300+ 个joint

struct Joint
{
    String		m_joint_name;
    UINT8		m_parent_joint_index;
    Translation	m_bind_pose_translation;
    Rotation	m_bind_pose_rotation;
    Scale		m_bind_pose_scale;
    Matrix4X3	m_inverse_bind_pose_transform;
};

骨骼 (Bone)：抽象的概念，每对父子关节之间的位移就是一段骨骼

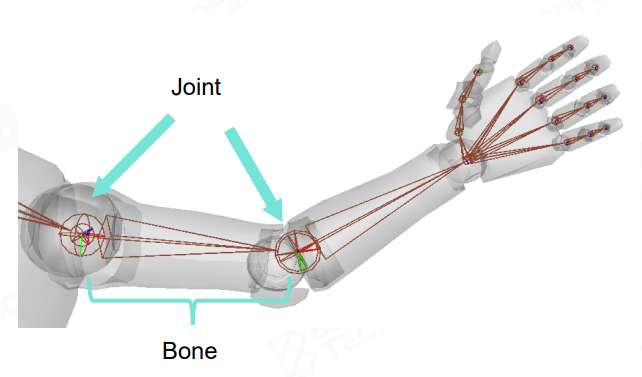
骨架 (skeleton)：其实就是多个 joint 组成的骨骼层次体系，用来管理 joints

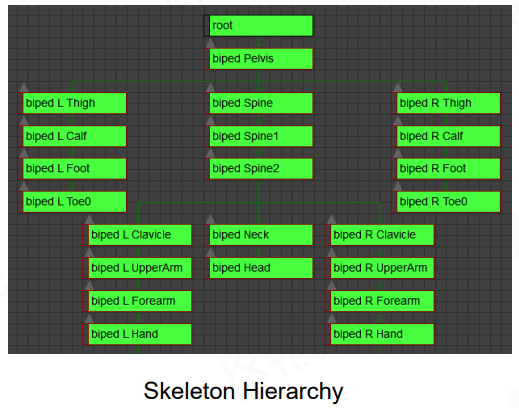
struct Skeleton
{
  UINT 		m_joint_count;	// number of joints
  Joint 	m_joints[];		// array of joints
};

以下是一些特殊的 joint：

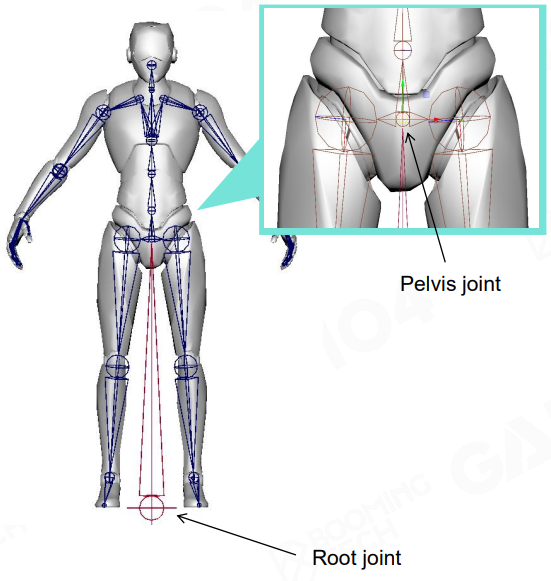
root joint: 双脚底的中心，方便贴合在地面上

pelvis joint: root joint 的第一个子关节，方便分离开上半身和下半身

weapon joint: 常常设置在武器把柄上，方便与 mount joint 贴合

mount joint: 常常设置在手上，方便与 weapon joint 贴合

蒙皮矩阵 (Skinning Matrix)

Local Space, Model Space, World Space

由于 joint 之间存在父子关系，因此也需要理清各个 space 的关系：

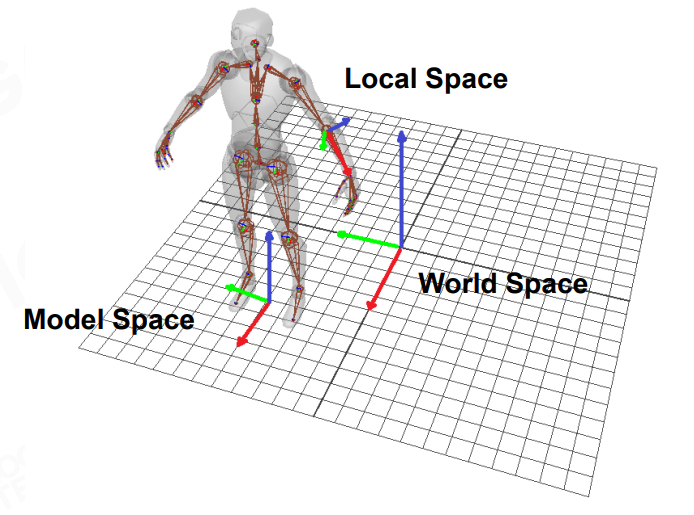
Local Space：相对于父节点（parent joint）的空间

Model Space：相对于根节点（root joint）的空间

World Space：相对于场景原点的空间

计算 Joint Pose Matrix

对于某个 joint $j$ ，它的 pose 实际上就是 Scale, Rotation, Translation 属性组成的变换：

M_{j}^{l o c a l} = T R S = [\begin{array}{cc} R S & T \\ 0 & 1 \end{array}]

$M^{local}_{j}=T R S=\left[\begin{array}{cc}RS & T \\ 0 & 1\end{array}\right]$

$M^{local}_{j}$ ：joint $j$ 的 local space pose

类似于模型变换，都有 SRT 属性，只不模型变换是对整个模型（例如整个角色）的 SRT 变换，而 joint pose 是局部到某个关节的 SRT 变换

然后，为了计算出 $j$ 的 model space pose，还得知道 $j$ 的 parent joint 的 model space pose，即：

M_{j}^{m o d e l} = M_{p (j)}^{m o d e l} M_{p (j)}^{l o c a l} = \prod_{x = p (j)}^{0} M_{x}^{l o c a l}

$M_{j}^{model}= M_{p(j)}^{model}M^{local}_{p(j)} = \prod_{x=p(j)}^{0} M_{x}^{local}$

$p(j)$ ：joint $j$ 的 parent joint

$M_{j}^{model}$ ： joint $j$ 的 model space pose

计算 Skinning Matrix

通常来说，DCC 在记录一个角色模型 mesh 的顶点时，会记录它们在 binding pose 下的 model space 位置而不是 local space 位置。

为此，如果需要用到顶点的 local space 位置，则必须通过下式计算出来（假定顶点 $V$ 只受该 joint $j$ 影响）：

V_{b}^{l o c a l} = {(M_{b (j)}^{m o d e l})}^{- 1} \cdot V_{b}^{m o d e l}

$V_{b}^{local}=\left(M_{b(j)}^{model}\right)^{-1} \cdot V_{b}^{model}$

$M_{b(j)}^{model}$ ： joint $j$ 的 model space binding pose

在实际每帧运行（第 $t$ 帧）中，假如我们已经通过逻辑驱动了 skeleton（或者说各个 joint）的变化。

那么要算出顶点的 model space 位置，就得通过下式：

V^{m o d e l} (t) = V_{j}^{m o d e l} (t) = M_{j}^{m o d e l} (t) \cdot V_{b}^{l o c a l} = M_{j}^{m o d e l} (t) \cdot {(M_{b (j)}^{m o d e l})}^{- 1} \cdot V_{b}^{m o d e l} $ ​

$V^{model}(t)=V^{model}_{j}(t)=M_{j}^{model}(t) \cdot V_{b}^{local}=M_{j}^{model}(t) \cdot\left(M_{b(j)}^{model}\right)^{-1} \cdot V_{b}^{model}$$

$\left(M_{b(j)}^{model}\right)^{-1}$ ：也可以叫 inverse binding pose matrix

由于 binding pose 是固定的，不会随着时间 $t$ 的变化而变化，因此可以在每个 joint 中计算一遍并存储对应的 inverse binding pose matrix ，以便之后每帧计算顶点 model space 位置直接读取使用，而不必重新计算一遍。

其实所谓的蒙皮矩阵，就是 $K_{j}=M_{j}^{model}(t) \cdot\left(M_{b(j)}^{model}\right)^{-1}$

为什么 DCC 的文件不记录成 local space 位置，明明这样还能省去逆矩阵的计算？

local space 位置实际上是耦合了 skeleton 信息和 mesh 信息，而采用蒙皮矩阵方式可以轻松将 skeleton 套在任意的 mesh 上（例如换个人物模型）

实际上蒙皮动画的顶点是受 N 个 joint 影响的，那这样一个顶点就要记录 N 个 local space 位置，大大增加模型文件的体积

加权 Skinning Matrix

当然在蒙皮动画中，顶点往往受多个 joint 影响，因此需要计算它们的加权和，得到的结果就是顶点 $V$ 的真正位置：

V^{m o d e l} (t) = \sum_{i = 0}^{N - 1} W_{i} \cdot V_{J_{i}}^{m o d e l} (t) $

$V^{model}(t)=\sum_{i=0}^{N-1} W_{i} \cdot V_{J_{i}}^{model}(t)$$

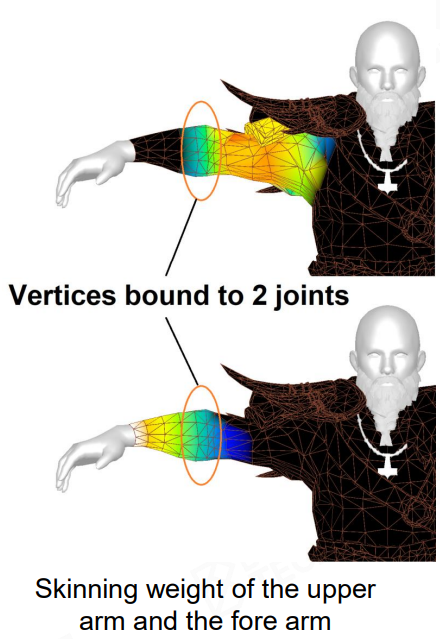
为什么顶点不设计成只受 1 个 joint 影响？

设计成受多个 joint 影响时，mesh 的变化会更加符合皮肤的特性，即可以在各种旋转扭曲等变化下保持肢体之间的连接性

若设计成只受 1 个 joint 影响，那么各个部位会看着像是一块块坚硬的刚体，且部位之间容易产生重叠、中空

Skinning Matrix Palette 优化

提前将各 joint 的蒙皮矩阵计算出来，形成一个 Skinning Matrix 数组送入 GPU 以供渲染使用

角色渲染的 vertex shader 也从以往的乘 $MVP$ 矩阵变成乘 $KM^{world}VP$ 矩阵
Skinning Matrix 的基础上再乘多一个 $M^{world}$ 来把 model space 转换成 world space

K_{j}^{'} = M^{w o r l d} \cdot M_{j}^{m o d e l} (t) \cdot {(M_{b (j)}^{m o d e l})}^{- 1}

$K_{j}^{\prime}=M^{world} \cdot M_{j}^{model}(t) \cdot\left(M_{b(j)}^{model}\right)^{-1}$

角色渲染的 vertex shader 也从以往的乘 $MVP$ 矩阵变成乘 $K^{\prime}VP$ 矩阵

动画插值

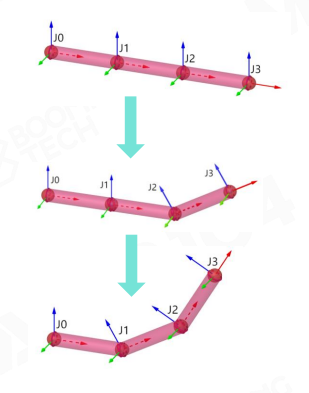
那么蒙皮动画该怎么驱动 skeleton 产生变化呢？

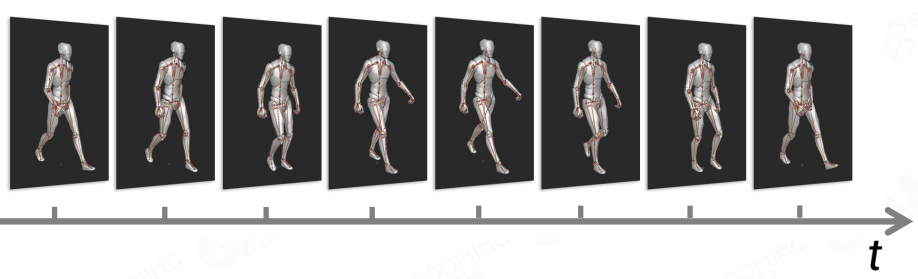
在每个关键帧上摆好一个 skeleton pose（这一系列的 skeleton pose 也被称为一个 Clip），然后再通过对前后两个关键帧 pose 的插值得到当前帧的 pose，也就是得到产生变化的 skeleton pose

注意：Joint Pose 插值应当在 local space 上进行，而不应当在 model space 上插值

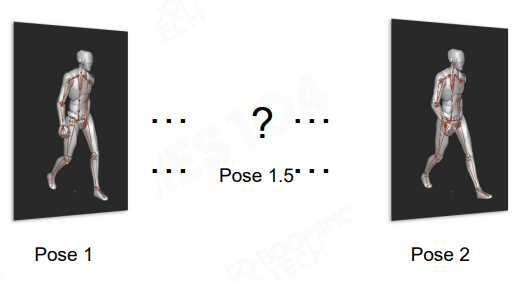
Translation & Scale 插值：LERP

对于 Translation 和 Scale 的插值，可以简单的使用 LERP（线性插值）。

Translation：

T (t) = (1 - a) T (t_{1}) + a T (t_{2})

$T(t)=(1-a) T\left(t_{1}\right)+a T\left(t_{2}\right)$

Scale：

S (t) = (1 - a) S (t_{1}) + a S (t_{2})

$S(t)=(1-a) S\left(t_{1}\right)+a S\left(t_{2}\right)$

$a=\frac{t-t_{1}}{t_{2}-t_{1}}, t_{1}<t_{2}, t \in\left[t_{1}, t_{2}\right]$

Rotation 插值：LERP, NLERP, SLERP

Rotation：

LERP（线性插值）
- 最直接的插值方式，可用于 Translation，Scale
- 但是往往不适用于 Rotation（四元数）插值
$q_{t}=\operatorname{Lerp}\left(q_{t 1}, q_{t 2}, t\right)=(1-a) q_{t 1}+a q_{t 2}$

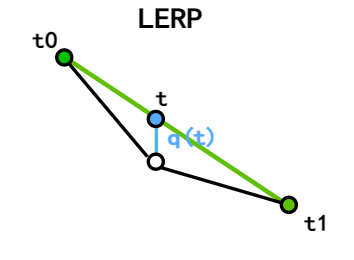
NLERP
- 插值的角速度是不固定的
- 当 $\theta$ 很小时，可以近似看成插值角速度相等

q_{t}^{'} = Nlerp (q_{t 1}, q_{t 2}, t) = \frac{(1 - a) q_{t 1} + a q_{t 2}}{‖ (1 - a) q_{t 1} + a q_{t 2} ‖}

$q_{t}^{\prime}=\operatorname{Nlerp}\left(q_{t 1}, q_{t 2}, t\right)=\frac{(1-a) q_{t 1}+a q_{t 2}}{\left\|(1-a) q_{t 1}+a q_{t 2}\right\|}$

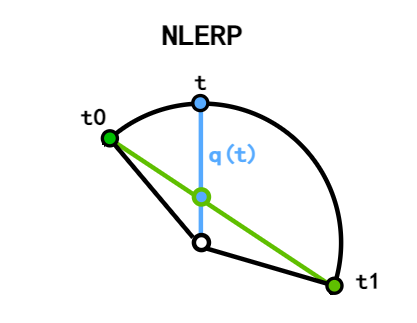
SLERP
- 插值的角速度是固定的
- 但当 $\theta$ 很小时，可能会出现零除问题
- 计算量稍大

q_{t} = Slerp (q_{t 1}, q_{t 2}, t) = \frac{\sin ((1 - t) θ)}{\sin (θ)} \cdot q_{t 1} + \frac{\sin (t θ)}{\sin (θ)} \cdot q_{t 2}

$q_{t}=\operatorname{Slerp}\left(q_{t 1}, q_{t 2}, t\right)=\frac{\sin ((1-t) \theta)}{\sin (\theta)} \cdot q_{t 1}+\frac{\sin (t \theta)}{\sin (\theta)} \cdot q_{t 2}$

$\theta=\arccos \left(q_{t 1} \cdot q_{t 2}\right)$

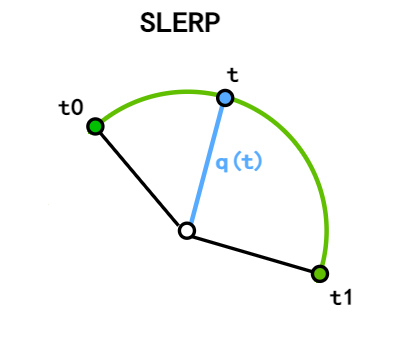
Rotation 插值方法结论：

当 $\theta$ 很小时，使用 NLERP 进行四元数插值
当 $\theta$ 很大时，使用 SLERP 进行四元数插值

动画压缩

减少 DoF（自由度）

scale：

可以舍弃 scale 属性（通常 joint 的 scale 是不会发生改变的，除了面部 joint）

translation：

可以舍弃 translation 属性（通常 joint 的 translation 是不会发生改变的，除了面部 joint，pelvis joint 等）

减少线性关键帧

当 Clip 中存在有一些关键帧 pose 和其前后关键帧 pose 插值结果相差不大时，我们可以移除掉这种关键帧，这样可以减少动画 Clip 的体积：

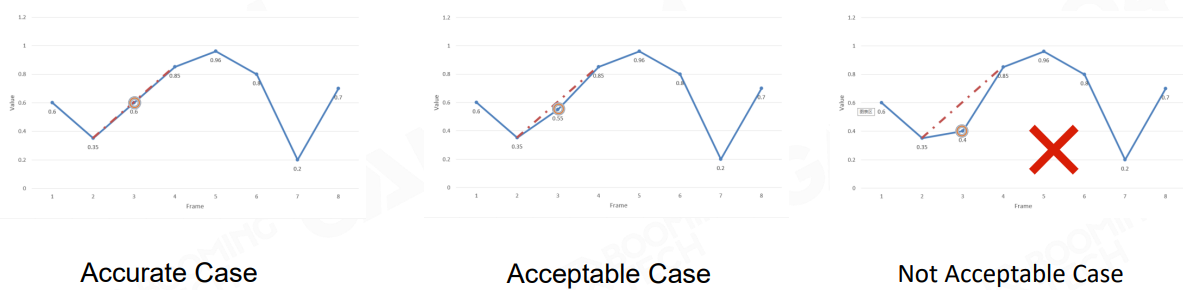
KeyFrame = {}
for i = 1 to n-1 do
    frame_interp = Lerp(frame[i-1], frame[i+1])
    error = Diff(frame[i], frame_interp)
    if isNotAcceptable(error) then
        KeyFrame.insert(frame[i])
	end
end

Catmull-Rom Spline 拟合动画曲线

现实捕捉出的动画往往是各种曲线的，如果默认用线性来拟合真实动画曲线（离线拟合），那么可能会产生大量关键帧。

而 Catmull-Rom Spline 可以用四个控制点（P0, P1, P2, P3）来生成一条从 P1 到 P2 的曲线，

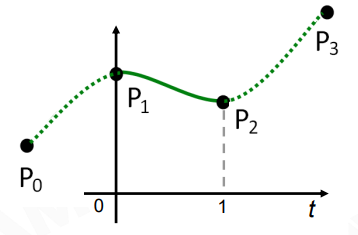
将其用于拟合真实动画可以节省大量关键帧：

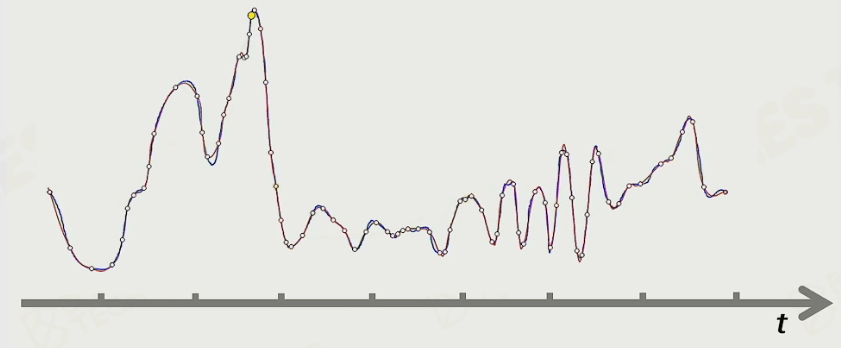
这样在 Clip 的关键帧间我们将通过下式计算出在 Catmull-Rom Spline 中的插值结果：

P (t) = [\begin{array}{llll} 1 & t & t^{2} & t^{3} \end{array}] [\begin{array}{cccc} 0 & 1 & 0 & 0 \\ - a & 0 & a & 0 \\ 2 a & a - 3 & 3 - 2 a & - a \\ - a & 2 - a & a - 2 & a \end{array}] [\begin{array}{l} P_{0} \\ P_{1} \\ P_{2} \\ P_{3} \end{array}]

$P(t)=\left[\begin{array}{llll}1 & t & t^{2} & t^{3}\end{array}\right]\left[\begin{array}{cccc}0 & 1 & 0 & 0 \\ -a & 0 & a & 0 \\ 2 a & a-3 & 3-2 a & -a \\ -a & 2-a & a-2 & a\end{array}\right]\left[\begin{array}{l}P_{0} \\ P_{1} \\ P_{2} \\ P_{3}\end{array}\right]$

$a$ 决定了曲线的弯曲程度有多尖锐（通常会设置 $a=0.5$ ）

Float Quantization

实际上动画中的各属性的 float 数值很少达到 float 可表达的最大范围（约 -3.4e+38 ~ 3.4e+38），因此我们可以先设定一个值域范围 $[v0, v1]$ ，然后均匀映射到更少位（如 16 位）的无符号整型范围上，这样的无符号整型中每相隔 1 就是代表了 $\frac{v1-v0}{2^{16}}$ 的数值（同时也代表了这种表示的精度）。

Scale：可以采用 16 位 float quantization（原始存储需要 32 位，即1个float）

Translation：可以采用 3 个 16 位 float quantization（原始存储需要 96 位，即3个float）

四元数：可以采用 48 位的存储方案（原始存储需要 128 位，即4个float）：

使用 2 位来表达哪个分量被丢弃了：即指明 X, Y, Z, W 哪个分量的绝对值最大，这样抛弃掉该分量后，可以由四元数性质通过 $1-\sum_{other}{scalar}^{2}$ 来推导出来

抛弃绝对值最大的分量，实际上就是保留绝对值较小的分量，这样做可以减少一些精度误差

使用 15 位来表达每个 float quantization ，值域范围在 $\left[-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right]$ ，精度便是 $\sqrt{2} / 32767 \approx 0.000043$

综上，原本一个 joint pose 需要存储 scale, translation, rotation 共 32 字节，用了 float quantization 后可以压缩成 14 字节。

动画误差

我们知道压缩动画必定会牺牲精度，如何让动画既能满足压缩性能又能满足视觉上的正确性（看起来没太大问题就是没问题）？那么我们需要通过离线方法去测量动画的误差并尽可能修正误差，在这些步骤完成后才可以将该动画文件交给玩家老爷们观赏。

误差传播

在动画压缩中，尤其要注意 误差传播：某个 joint pose 产生了误差，那么它的 child joint 会进一步放大这个误差，并且 child 的 child 会递归式地继续放大误差...

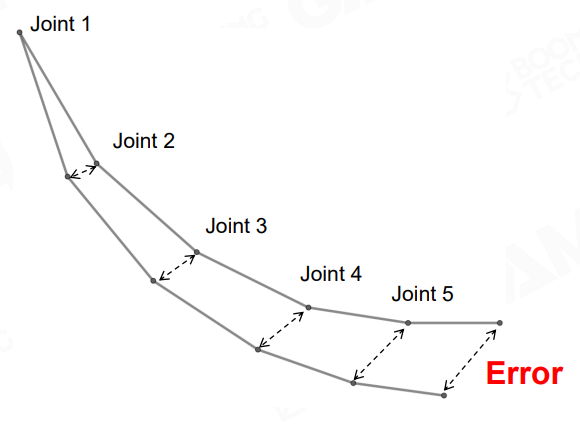
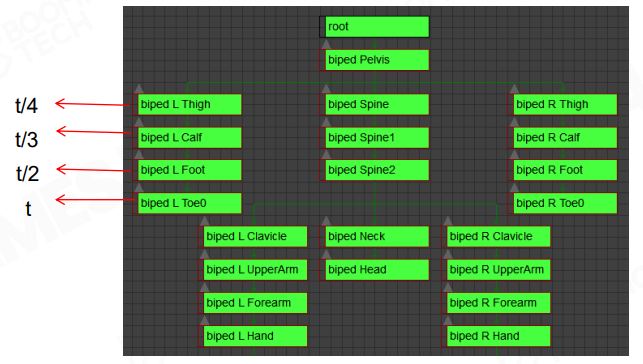
也就是说每个 joint 的误差容忍能力是不同的，而且越靠近 root 的 joint 误差容忍能力越低，反之越接近叶节点的 joint 误差容忍能力越强。我们可以根据 skeleton 层级来决定每个 joint 结点的最大误差

图中叶节点的最大误差值为 $t$

误差测量

通过观测视觉上的动画错误来测量误差是低效率的，而且往往容易看漏。

可以在每个 joint 的两个正交方向上分别放置 Fake Vertex，测量出压缩前和压缩后的 Fake Vertex 位置差，这个位置差便是动画误差：

角色骨骼的 Fake Vertex 一般放置在距离 joint 2~10 cm 的地方
长物体一般放置在距离 joint 1~10 m 的地方

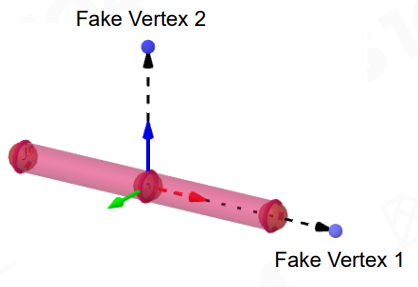
为什么 joint 得放置两个正交方向上的 Fake Vertex，而不是一个 Fake Vertex？

例如在下面情形，joint 出现旋转误差，单个方向上的 Fake Vertex 是无法测量出来的：

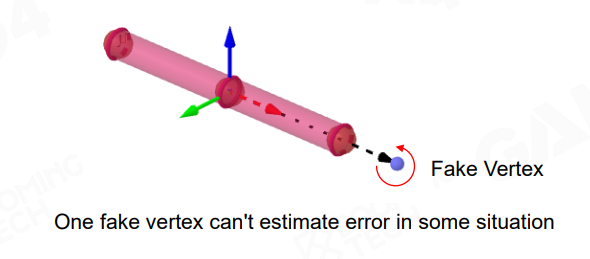
误差补偿

假设在某一关键帧中，parent joint pose 因压缩产生的误差被测量了出来，那么在当前 joint pose 可以做一些反向补偿：例如直接修改当前 joint pose 反向增加该误差值并更新到当前 joint pose

$Pose_{j} := Pose_{j}-Error(Pose_{p(j)})$

当然，当前 joint pose 仍然还是会产生误差，但是抵消了它上一级的误差，因此它的 child joint pose 仍然可以继续使用误差补偿来抵消这一级的误差，从而最终让各级压缩的 joint pose 更加贴合精确 joint pose

但是它也是有缺点的：

初始的 joint pose 动画是平滑的、低频的，但是引入误差补偿，实际上就是引入高频信息，因此越到末端的 joint 越容易出现一些奇怪的抖动（例如末端的肢体可能会发生高频的抽搐抖动）

参考

[1] GAMES104-现代游戏引擎：从入门到实践

个人感想：所谓动画，核心实际上就是压缩，即如何用有限的计算机数据表现现实生活中栩栩如生的角色动画（压缩大小与压缩质量的平衡）。例如只记录关键帧而不记录每一帧，中间帧通过插值计算出来就是一种压缩现实数据的方式；用几十个 joint 组成的 skeleton 来表示人体骨骼也是一种简化现实数据的方式；插值方式, 压缩方法, 误差补偿等等...无一不是为了这两个方面去服务

posted @ 2022-06-10 17:01 KillerAery 阅读(2809) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 实时&离线皮肤渲染技术（Real-time & Offline Skin Rendering）

· 实时光线追踪（2）Denoising: Nvidia Real-time Denoiser 剖析

· 游戏动画技术简介

· C++-游戏动画编程实用指南（全）

· 转:骨骼动画教程及微软示例Skinned Mesh的解析(一)

阅读排行：
· 全程不用写代码，我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了，比商业数据库还牛
· 白话解读 Dapr 1.15：你的「微服务管家」又秀新绝活了

KillerAery