洛谷 - P1852 跳跳棋 题解
题目链接
实际难度
\(\color{4169E1}{省选/NOI-}\)
考察知识点
-
图论 - 树上问题 - 最近公共祖先
-
算法 - 二分
思路分析 Part.1
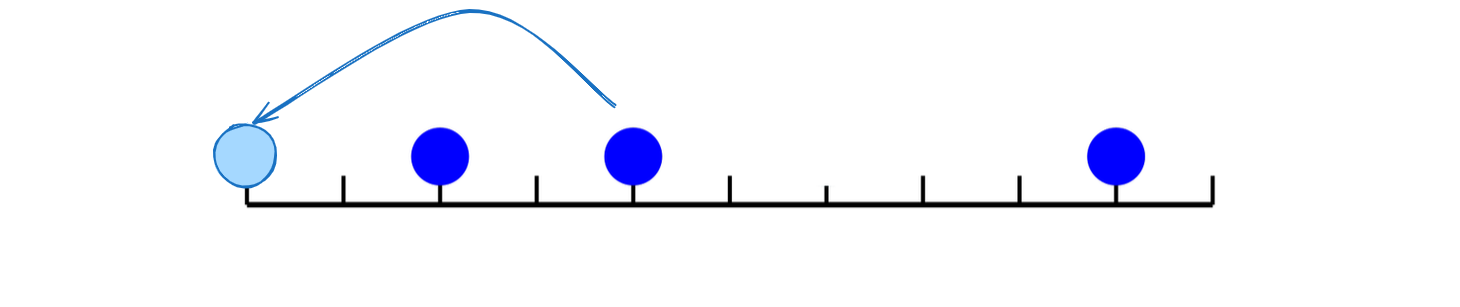
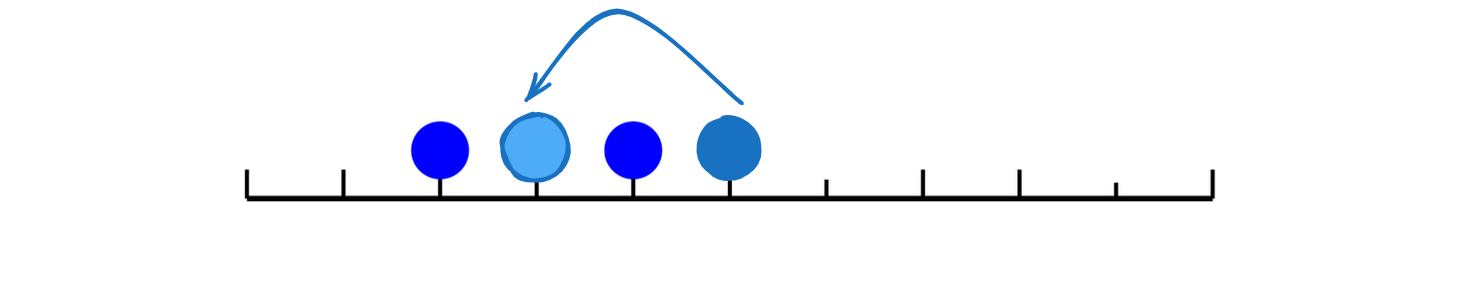
根据题意我们可以发现,跳跳棋移动的情况只有四种,分别是:
可以发现,状态 \((x,y,z)\) 经“中间的点往两边跳”后的状态 \((u,v,w)\) 等价于状态 \((u,v,w)\) 经“两边的点往中间跳”后的状态 \((x,y,z)\)。
可以把状态 \((u,v,w)\) 和状态 \((x,y,z)\) 之间连一条无向边,这样本题第一问就转化为当前棋子的位置状态和目标位置状态是否存在最近公共祖先,第二问就转化为当前棋子的位置状态和目标位置状态的简单路径的长度。
看一眼数据规模:对于100%的数据,绝对值不超过\(10^9\)。如果按照上面的过程建出一个树来,无法通过。因此考虑优化。
回顾一下倍增求最近公共祖先的过程:
-
预处理阶段:通过一次深搜,记录每个节点的深度,并预处理一个重要的数组
fa[node][i]。这个数组的含义是:节点node向上跳 \(2^i\) 步所到达的祖先节点。 -
查询阶段:对于任意两个节点 \(u\) 和 \(v\),通过
fa数组进行“跳跃”操作,先将它们调整到同一深度,然后一起向上跳,直到找到它们的最近公共祖先。
可以发现,倍增求最近公共祖先的核心就是处理向上跳 \(k\) 步后的状态,因此,我们决定优化这一步骤。
令 \(u=y-x,v=z-y\),当左右距离 \(u\) 和 \(v\) 不相等时,可连续跳跃多次。
若 \(u \lt v\),左边棋子可向右跳 \(k=min(\lfloor {\frac{v-1}{u}} \rfloor,s)\) 次(\(s\) 为剩余步数上限),直接更新状态为 \((x+k \times u,y+k \times u,z)\)。
若 \(u \gt v\),右边棋子可向左跳 \(k=min(\lfloor {\frac{u-1}{v}} \rfloor,s)\) 次(\(s\) 为剩余步数上限),直接更新状态为 \((x,y-k \times v,z-k \times v)\)。
为什么这样可行?
思路分析 Part.2
连续跳跃的可行性
当三个棋子的位置为 \((x,y,z)\)(满足 \(x \le y \le z\))时,左右两边的距离分别为:
- 左边距离 \(u=y-x\)(左到中)
- 右边距离 \(v=z-y\)(中到右)
情况 1:\(u \lt v\)(左边距离小于右边距离)
此时,左边的棋子 \(x\) 可以向右跳(属于 “两边向中间跳” 的规则),跳跃后新位置为:
- 原中间棋子 \(y\) 成为新的左端点;
- 原左棋子 \(x\) 跳至 \(2y - x\)(新的中间点);
- 右端点 \(z\) 不变。
新状态排序后为 \((y,2y-x,z)\),此时新的距离为:
- 新左边距离:\((2y-x)-y=y-x=u\)(与原左边距离相等);
- 新右边距离:\(z-(2y-x)=(z-y)-(y-x)=v-u\)(右边距离减少了 \(u\))。
每次左边棋子向右跳时,左边距离 \(u\) 保持不变,而右边距离 \(v\) 会减少 \(u\)(即\(v_{新}=v_{旧}- u\))。 只要 \(v_{新} \gt u\),就可以继续重复这个跳跃过程(因为此时仍然满足 \(u \lt v_{新}\))。
情况 2:\(v \lt u\)(右边距离小于左边距离)
类似地,右边的棋子 \(z\) 可以向左跳,跳跃后新位置排序为 \((x,2y-z,y)\),此时:
- 新右边距离:\(y-(2y-z)=z-y=v\)(与原右边距离相等);
- 新左边距离:\((2y-z)-x=(y-x)-(z-y)=u-v\)(左边距离减少了 v)。
同样,只要 \(u_{新} \gt v\),就可以连续跳跃。
证毕
跳跃次数计算的合理性
连续跳跃的次数 \(k\) 受两个限制:
- 不能超过剩余允许的最大步数 \(s\);
- 不能跳至 “无法继续同方向跳跃” 的状态(即跳 \(k\) 次后,需保证下一次跳跃不再满足同方向条件)。
当 \(u \lt v\) 时:
每次跳跃后右边距离减少 \(u\),经过 \(k\) 次跳跃后,右边距离变为 \(v - k \times u\)。 为了保证 “跳 \(k\) 次后无法再继续同方向跳跃”,需满足:\(v - k \times u \lt u\) (即跳 \(k\) 次后右边距离小于左边距离,下一次跳跃方向改变)。
整理得:\(k \times u \gt v - u \implies k \gt \frac{v-u}{u} \implies k \ge \lfloor \frac{v - 1}{u} \rfloor\)
这里用 \(v - 1\) 是为了取最大整数 \(k\)(例如 \(v=5, u=2\) 时,\((5-1)/2=2\),即最多跳 2 次,跳后右边距离为 \(5 - 2 \times 2 = 1 \lt 2\),符合条件)。
当 \(v \lt u\) 时:
类似地,每次跳跃后左边距离减少 \(v\),经过 \(k\) 次跳跃后,左边距离变为 \(u - k \times v\)。 需满足:\(u - k \times v \lt v \implies k > \frac{u - v}{v} \implies k \ge \lfloor \frac{u - 1}{v} \rfloor\)。
证毕
之后二分从a到a和b的最近公共祖先的距离ans,即可求出答案,为\(2 \times ans+(dep1-dep2)\)。
复杂度分析
时间复杂度
空间复杂度
- 主要存储:\(O(1)\)
- 临时变量:\(O(1)\)
- 总空间:\(O(1)\)
C++代码
无注释代码
// Problem: P1852 跳跳棋
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1852
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include <cstdio>
#include <algorithm>
struct Node{
int x,y,z;
void init(){
scanf("%d%d%d",&x,&y,&z);
if(x>y) std::swap(x,y);
if(x>z) std::swap(x,z);
if(y>z) std::swap(y,z);
};
};
bool equal(Node a,Node b){
return a.x==b.x&&a.y==b.y&&a.z==b.z;
}
Node transform(Node t,int s,int &l){
l=0;
while(s>0){
int u=t.y-t.x,v=t.z-t.y;
if(u==v) break;
int k;
if(u<v){
k=std::min((v-1)/u,s);
t.x+=k*u,t.y+=k*u;
}else{
k=std::min((u-1)/v,s);
t.y-=k*v,t.z-=k*v;
}
l+=k;
s-=k;
}
return t;
}
int main(){
Node a,b;
a.init(),b.init();
int dep1,dep2;
Node p=transform(a,1e9,dep1),q=transform(b,1e9,dep2);
if(!equal(p,q)) puts("NO");
else{
if(dep1<dep2) std::swap(dep1,dep2),std::swap(a,b);
int tmp;
a=transform(a,dep1-dep2,tmp);
int l=0,r=dep2,ans=0;
while(l<=r){
int mid=(l+r)/2;
if(equal(transform(a,mid,tmp),transform(b,mid,tmp))){
r=mid-1;
ans=mid;
}else l=mid+1;
}
printf("YES\n%d\n",2*ans+(dep1-dep2));
}
return 0;
}
有注释代码
// Problem: P1852 跳跳棋
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1852
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include <cstdio>
#include <algorithm>
// 定义Node结构体,存储三个棋子的位置(保证x<=y<=z有序)
struct Node{
int x, y, z; // 分别存储左、中、右三个棋子的位置(已排序)
// 初始化函数:读取三个棋子位置并排序,确保x<=y<=z
void init(){
scanf("%d%d%d", &x, &y, &z); // 读取原始位置
// 冒泡排序调整顺序,保证左小右大
if(x > y) std::swap(x, y);
if(x > z) std::swap(x, z);
if(y > z) std::swap(y, z);
}
};
// 判断两个状态是否完全相同(三个棋子位置一致)
bool equal(Node a, Node b){
return a.x == b.x && a.y == b.y && a.z == b.z;
}
// 状态转换函数:将状态t向根状态(无法再批量跳动的状态)归约
// 参数t:待转换的状态;s:最多允许跳动的步数;l:输出参数,记录实际跳动的步数
// 返回值:转换后的状态
Node transform(Node t, int s, int &l){
l = 0; // 初始化实际跳动步数为0
while(s > 0){ // 只要还有剩余允许的步数
int u = t.y - t.x; // 左、中棋子的距离
int v = t.z - t.y; // 中、右棋子的距离
if(u == v) break; // 若左右距离相等,无法再批量跳动,退出循环
int k; // 本次批量跳动的步数
if(u < v){ // 左中距离小,左棋子可跳过中棋子,批量向右跳
// 计算最大可跳步数:(v-1)/u 确保跳动后不超过右棋子,同时不超过剩余步数s
k = std::min((v - 1) / u, s);
t.x += k * u; // 左棋子向右移动k*u(跳过k次中棋子)
t.y += k * u; // 中棋子向右移动k*u(保持与左棋子距离不变)
}else{ // 中右距离小,右棋子可跳过中棋子,批量向左跳
k = std::min((u - 1) / v, s);
t.y -= k * v; // 中棋子向左移动k*v
t.z -= k * v; // 右棋子向左移动k*v
}
l += k; // 累计实际跳动步数
s -= k; // 减少剩余允许步数
}
return t; // 返回归约后的状态
}
int main(){
Node a, b; // a:初始状态,b:目标状态
a.init(); // 读取并初始化初始状态
b.init(); // 读取并初始化目标状态
int dep1, dep2; // dep1:初始状态到根状态的步数,dep2:目标状态到根状态的步数
// 将初始状态和目标状态分别归约到根状态(最多跳1e9步,确保归约到底)
Node p = transform(a, 1e9, dep1);
Node q = transform(b, 1e9, dep2);
if(!equal(p, q)){ // 若根状态不同,说明无解
puts("NO");
}else{ // 根状态相同,存在解
// 调整初始状态和目标状态的深度,让a的深度 >= b的深度
if(dep1 < dep2){
std::swap(dep1, dep2);
std::swap(a, b);
}
int tmp; // 临时变量,存储transform的实际步数(无用,仅占位)
// 将a状态向上归约dep1-dep2步,与b状态处于同一深度
a = transform(a, dep1 - dep2, tmp);
int l = 0, r = dep2, ans = 0; // 二分查找公共祖先的步数
while(l <= r){
int mid = (l + r) / 2; // 二分中点:尝试跳mid步
// 分别将a和b向上归约mid步,判断是否到达同一状态
if(equal(transform(a, mid, tmp), transform(b, mid, tmp))){
r = mid - 1; // 找到更优解,向左缩小范围
ans = mid; // 记录当前有效mid(公共祖先步数)
}else{
l = mid + 1; // 未到达同一状态,向右扩大范围
}
}
// 总步数 = 初始状态到公共祖先的步数 + 目标状态到公共祖先的步数
// 初始到公共:(dep1-dep2) + ans;目标到公共:ans;总和为 2*ans + (dep1-dep2)
printf("YES\n%d\n", 2 * ans + (dep1 - dep2));
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号