【RL系列】马尔可夫决策过程——状态价值评价与动作价值评价
请先阅读上两篇文章:
状态价值函数,顾名思义,就是用于状态价值评价(SVE)的。典型的问题有“格子世界(GridWorld)”游戏(什么是格子世界?可以参考:Dynamic programming in Python),高尔夫游戏,这类问题的本质还是求解最优路径,共性是在学习过程中每一步都会由一个动作产生一个特定的状态,而到达该状态所获得的奖励是固定的,与如何到达,也就是之前的动作是无关的,并且这类问题都有一个或多个固定的目标。相比较而言,虽然Multi-Armed Bandit(MAB)问题也可以用状态价值评价的方法进行policy的求解,不过这个问题本质上还是对动作价值的评价。因为在MAB问题中,一个动作只能产生固定的状态,且一个状态只能由一个固定的动作产生,这种一对一的关系决定了其对动作的评价可以直接转化为状态评价。一个典型的SVE问题在转变为动作价值评价(AVE)问题时(前提是这种转变可行),往往奖励机制会发生变化,从对状态奖励转变为对当前状态的某一动作奖励,因为MAB问题的动作状态等价,所以这种变化并不明显,本篇也就不再将MAB问题作为讨论的例子了。本篇将着重分析一个典型的SVE问题和一个典型的AVE问题,从而引出SVE与AVE在马尔可夫决策过程下的统一形式。
这里需要强调一点的是,bellman方程实质上是由AVE的思想引出,与之前我在文章 【RL系列】马尔可夫决策过程与动态编程 中所给出的状态价值评价的推导逻辑还是有些许不同的,所以bellman方程并不适合统一这两种评价体系。如果想要详细了解bellman方程,我认为看书(Reinforcement Learning: An Introduction)和阅读这篇文章 强化学习——值函数和bellman方程 都是不错的选择。
GridWorld
简单介绍一下“格子世界”游戏。这是一个非常简单的寻找最优路径的问题,也是一个典型的SVE问题。给定一个有N*N个网格的地图,在这些网格中有一个或几个目的地,找出地图上任意一个网格到达最近目的地的最短路径。举个例子,如下4x4地图,图中的X即为目的地,A为agent,GridWorld研究的问题就是找到A到达X的最短路径,注意A每回合只能上下左右前进一格:
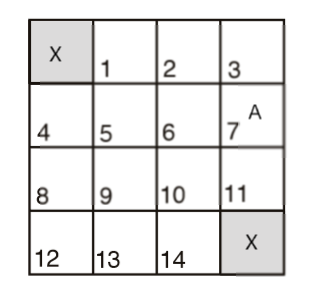
用状态价值评价的方式解决GridWorld问题:
- 将该地图中的16个格子分别记为16种状态,建立奖励机制,给出各个状态的奖励:目的地状态奖励设为1,其它状态奖励设为0,其奖励矩阵可以写为$ \mathbf{R} $: $$ \mathbf{R} = \left[ \begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}\right] $$
- 使用状态价值评价函数求解每个状态收敛时的价值。
- 依据各个状态的价值制定policy,以greedy-policy为例,每次做出前往当前状态周边价值最大的状态的动作。
用bellman方程(AVE)解决GridWorld问题:
- 在迭代过程中,记Agent每做一个动作,奖励为-1
- 目的地的动作选择概率设为0,即在目的地则不作任何动作
- 使用bellman方程来收敛计算价值评价
- 通过动作价值或状态价值计算policy
可以发现两者的不同主要体现在奖励机制的不同,奖励机制的不同也影响了价值评价函数的不一样。bellman方程所使用的奖励机制为动作奖励机制,即给每个动作规定该动作可以获得的奖励,这是典型的AVE的思想。AVE和SVE的最大不同点在于,SVE是用当前状态所获得的奖励与未来可能到达的状态的价值(未来价值)去评价当前状态的价值,而AVE是用未来可能动作价值的期望去评价当前状态的价值,而未来动作价值的期望又是由未来可能奖励的期望与未来可能状态的价值期望的线性组合。
简单来说,SVE的价值更新函数为,其中$ \mathbf{V}' $表示未来状态的价值期望:
$$ \mathbf{V}(s) = \mathbf{R}(s) + \gamma \mathbf{V}' $$
AVE的价值更新函数可以写为:
$$ \mathbf{V} = \sum_{a} \pi(a) \mathbf{Q}(a) $$
其中$ \mathbf{Q}(a) $表示未来可能的动作a的价值评价函数,$\pi(a)$表示动作a的选择概率。$ \mathbf{Q} $ 可以用动作奖励$ \mathbf{R} $与该动作可能的未来状态价值期望$ \mathbf{V}' $的线性组合表示:
$$ \mathbf{Q}(a) = \mathbb{R}(a) + \gamma \mathbf{V}' $$
两个算法在解决效率上几乎没有差别。只是对典型的SVE问题来说,使用SVE方法解决显得更加简洁,AVE稍显复杂但也未尝不可。然而对于典型的AVE问题来说,SVE方法就显得力不从心了。
Recycling Robot
“回收机器人”是一个典型的动作价值评价问题,如需详细了解这个问题,可以阅读Reinforcement Learning: An Introduction(2017)中的第三章。执行主体为回收机器人,其状态可分为两种,高电量状态(Hight)和低电量状态(Low)。可选择的动作有三种,搜索(Search),等待(Wait)和充电(Recharge)。不同的动作也会依一定的概率分布产生新的状态。为了更直观的理解这个问题,这里我们可以画出Recycling Robot的状态转移图像:
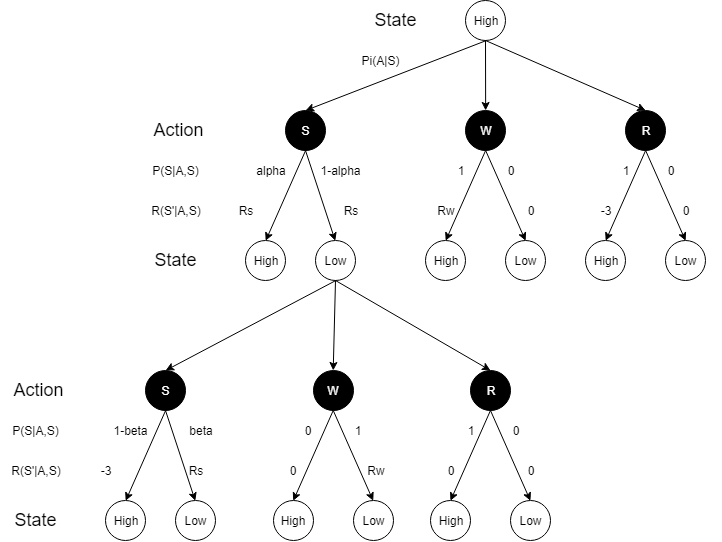
由于在这个问题里,动作与状态不仅不能够实现一一对应,而且该决策过程并没有一个或多个的目标状态,是无法使用SVE方法来解决这个问题的,但bellman方程确是合适的。“回收机器人”的目的并非达到某个目的状态,而是做出符合获取最大利益的决策(动作),所以下面我将给出具体的状态转移概率矩阵与动作奖励矩阵,尝试解决这个决策问题。
- 设$ \alpha = 0.8 $,也就是说在High状态下做出Search动作可保持High状态的概率为0.8,所以电量降低到Low状态的概率为0.2,此时的奖励两者皆为$ R_s = 1 $
- 设$ \beta = 0.15 $,说明在Low状态下做出Search动作可保持Low状态的概率为0.15,获得的奖励为$ R_s = 1 $。没电宕机的概率为0.85,此时需要人为救助重新回到High状态,奖励为$ R_s = -3 $
- 设在两种装填下选择Wait动作可获得的收益为$ R_w = 0.5 $,注意在做Wait动作后,当前状态不会改变,可以保持。
- Recharge动作可以使得当前状态转变为High状态。在High状态下做Recharge动作获得的奖励为$ R_r = -3 $,在Low状态下做Recharge动作不获得任何奖励,记$ R_r = 0 $
依据上述四点假设,我们可以写出动作-状态转移概率矩阵$ \mathbf{P}(a, s', s) $与动作奖励矩阵$ \mathbf{R}(s',a,s) $:
$$ \begin{align} & R(High) & = \left[\begin{matrix} 1 & 0.2 & -3\\ 1 & 0 & 0 \end{matrix}\right]\\ & R(Low) & = \left[\begin{matrix} -3 & 0 & 0\\ 1 & 0.2 & 0 \end{matrix}\right]\\ &P(High) &= \left[\begin{matrix} 0.8 & 0.2 \\ 1 & 0 \\ 1 & 0 \end{matrix}\right]\\ &P(Low) &= \left[\begin{matrix} 0.15 & 0.85 \\ 0 & 1 \\ 1 & 0 \end{matrix}\right] \end{align} $$
可以将(1),(2)式和(3),(4)式合成张量$\mathbf{R}_{s',a}^{s}$和张量$ \mathbf{P}_{a, s'}^s $:
$$ \mathbf{R} = \mathrm{fold}\left[\begin{matrix} R(High)\\R(Low) \end{matrix}\right]\\ \mathbf{P} = \mathrm{fold}\left[\begin{matrix} P(High)\\P(Low) \end{matrix}\right]$$
如果需要计算在Low状态下的未来可能奖励的期望$ \mathbb{R} $,用动作-状态转移概率$P(Low)$与动作奖励$ R(Low) $做矩阵相乘后取对角线即可:
$$ \mathbb{R} = \mathbb{E}(A|S = Low) = \mathrm{diag}\left(\left[\begin{matrix} 0.15 & 0.85 \\ 0 & 1 \\ 1 & 0 \end{matrix}\right] \left[\begin{matrix} -3 & 0 & 0\\ 1 & 0.2 & 0 \end{matrix}\right] \right) = \left[ \begin{matrix} -2.4\\ 0.2\\ 0\end{matrix}\right]$$
至此我们可以写出bellman方程的一般形式:
$$ \begin{align} &\mathbf{V} = \mathbf{\Pi} \mathbf{Q} \\ &\mathbf{Q} = \mathrm{diag}(\mathbf{P}\mathbf{R}) + \gamma \mathbf{P}\mathbf{V}' \end{align}$$
统一形式
首先,我们需要了解的一点就是,bellman方程所评价的状态价值的来源全部都是未来的期望,也就是说,bellman方程是与当前状态所获得的奖励是无关的。如果我们将bellman方程所得到的状态价值评价作为SVE里的未来可能状态价值的期望是绝对可行的!这样的话,SVE与bellman方程的统一形式可以写为:
$$\begin{align} & \mathbf{V} = \mathbf{R}_{s} + \gamma \mathbf{\Pi}\mathbf{Q} \\ & \mathbf{Q} = \mathrm{diag}(\mathbf{P} \mathbf{R}_{s', a}^{s}) + \gamma \mathbf{P} \mathbf{V}' \end{align}$$
其中$ \mathbf{R}_s $指的是当前状态所获得的奖励,$ \mathbf{R}_{s', a}^{s} $指的是在当前状态下执行动作a到达状态s’所得到的奖励。
通过更改$ \mathbf{R}_s $矩阵中对于特定状态的奖励,我们可以获得在某些特殊状况下的policy。比如在GridWorld中,如果有规定某个格子是障碍,不能通过(或可以规定为几乎不可能通过),在应用bellman方程时,需要更改动作-状态转移矩阵或动作奖励矩阵中的8个元素(出入障碍格子的8个动作),而在统一形式中,只需规定该状态的奖励为负值即可。假设障碍状态为$ S_b $,则可以设$ \mathbf{R}(S_b) = -100 $,这样在预处理上就比bellman方程方便许多。
再比如,对于Recycling Robot问题,通过改变High状态和Low状态的状态奖励,也可以在Policy上做出改变。用bellman+softmax求解出的动作选择policy如下(gamma = 0.5,温度系数tau = 0.5):
$$ \pi = \begin{matrix} H\\L \end{matrix} \left[\begin{matrix} P(\mathrm{Search}) & P(\mathrm{Wait}) & P(\mathrm{Recharge}) \\ P(\mathrm{Search}) & P(\mathrm{Wait}) & P(\mathrm{Recharge}) \end{matrix}\right] =\left[\begin{matrix} 0.8198 & 0.1799 & 0.0003\\0.0039 & 0.4937 & 0.5024\end{matrix}\right] $$
可以发现,当电量状态为Low时,机器人执行Wait和Recharge的概率是基本相同的,皆为50%左右。如果我们给High状态和Low做一个评价,比如到达High状态,奖励为1,到达Low状态不奖励,即奖励为0,使用统一形式得到的policy为:
$$ \pi = \left[\begin{matrix} 0.7879 & 0.2118 & 0.0004\\ 0.0049 & 0.2614 & 0.7337 \end{matrix}\right] $$
可以发现,当电量状态为Low时,机器人更加倾向于选择Recharge动作(概率为73.37%)回到状态High。如果Low状态的奖励为1,High状态的奖励为0,可以得到的policy为:
$$ \pi = \left[\begin{matrix} 0.8514 & 0.1483 & 0.0002\\0.0022 & 0.7552 & 0.2426 \end{matrix}\right] $$


 浙公网安备 33010602011771号
浙公网安备 33010602011771号