【RL系列】MDP与DP问题
推荐阅读顺序:
Reinforcement Learning: An Introduction (Drfit)
本篇
马尔可夫决策过程
马尔可夫决策(MDP)过程为强化学习(RL)提供了理论基础,而动态编程(DP)为马尔可夫决策过程提供了一种实现的方法。所以将这两个部分结合在一起去学习,我认为是非常合适的。
在之前的Multi-Armed Bandit(MAB)问题中,RL作为一种方法被用来估计一种状态下不同动作收益均值。在这个问题里,不同的动作只会产生不同的收益,状态看起来没有改变且下一次的可选择动作也不会发生改变。说状态不变有些许的不严谨,MAB问题实际上应该是一个自我状态不断更新的MDP。对于一个K-lever问题,严格上来说,是K个状态之间的不断转换。
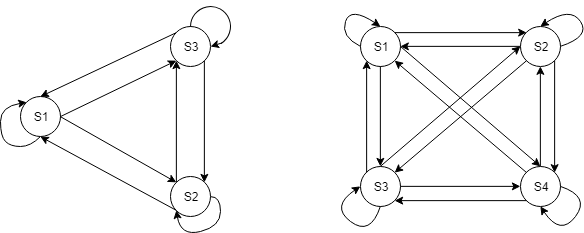
左图为3-lever的状态转移情形,右图为4-lever的状态转移情形。其中的状态转移表示着一个状态执行完一个动作后转变为另一个状态。举个例子,在3-lever的情形中,如果当前状态$ S_1 $,在拉动第三个lever后,转变为$ S_3 $。在状态转移的过程中,对动作选择需要服从的规则称为policy。
在MAB问题中,我们了解到,可以通过估计各个动作产生的收益均值来生成policy,这属于动作价值评价。在MDP中我们可以通过评价各个状态的价值来产生policy,通常来说,一个状态的价值越高,那么从另一个状态转移到这个状态所获得的收益也就越高。如果在状态转移过程中,每次都选择转移到下一个价值最高的状态,这样的policy就可以称为greedy policy(多说一句,相比较于动作评价,通过状态评价产生的greedy policy是比较安全的)。一个状态的价值通常由这个状态当前的奖励(Reward)与这个状态可以转移到的其它状态的价值所决定,后一个也可称为一个状态的未来价值(Future Value)。在MDP中,从一个状态转移到另一个状态可以由下图表示:
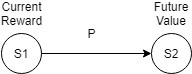
Current Reward表示当前在状态$ S_1 $所获得的奖励,Future Value表示状态$ S_2 $的价值,从$ S_1 $转移到$ S_2 $的概率为P,那么状态$ S_1 $关于状态$ S_2 $的价值计算可以写为:
$$ \mathbb{Value}(S_1|S_2) = \mathbb{Reward}(S_1) + \gamma P(S_1\to S_2) \mathbb{Value}(S_2) $$
如果$ S_1 $可能转移的状态为$ S_i $,$ i\in \{2, 3, ..., N \} $,转移至$ S_i $的概率为$ P(S_1 \to S_i) $,那么$ S_1 $当前的价值估计就可以表示为:
$$ \mathbb{Value}(S_1) = \mathbb{Reward}(S_1) + \gamma \sum_{i = 2}^{N} P(S_1\to S_i) \mathbb{Value}(S_i) $$
这里的$ \gamma $表示折扣系数,通常来说, $ \gamma $越大表示未来价值占价值估计的比重越高,当前奖励的比重越低。同时我们也可以发现,对状态价值的评估实际上就是当前价值与未来价值的一个平衡,这里的未来价值在数学上被定义为对所有可能转移状态的价值的期望。
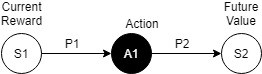
状态转移在RL中实际上分为两个部分,第一是动作选择部分,第二是动作后产生的结果。如果使用状态转移图,可以表示为:
这里的$ P_1 $也就是我们在MAB问题中已经讨论多次的动作选择概率(包括epsilon-greedy策略,UCB策略和Softmax策略等都是用来解决优化这个问题的)。我们用$ \pi(A_i | S_1) $来表示在状态$ S_1 $下选择动作$ A_1 $的概率。$ P_2 $则代表了在状态$ S_1 $下选择动作$ A_1 $产生并产生结果$ S_2 $的概率,通常使用$ P(S_2|A_1, S_1) $来表示。对于转移状态为多个的情况,可以将状态$ S_1 $的价值估计写为:
$$ \mathbb{Value}(S_1) = \mathbb{Reward}(S_1) + \gamma \sum_{i = 1}^{n} \pi(A_i|S_1)\sum_{j = 1}^{N(A_i)}P\left[S_{A_i}(j)|A_i, S_1\right] \mathbb{Value}\left[S_{A_i}(j)\right] $$
在这个式子中,$ N(A_i) $表示在动作$ A_i $下可能产生的状态总数,$ S_{A_i}(j) $表示在动作$ A_i $下的第$ j $个状态。强调一点,该式与Bellman equation并不完全一致,这里将Reward部分单独拿了出来,我是觉得这种形式更符合状态价值评价的推导逻辑。给出这个式子所对应的状态转移图,以便于更好的理解:
动态编程
这种不断产生分支的状态转移图又可以称为树状图(State-Action-State Backup Diagram),此外还有Action-State-Action树状图用于分析动作评价方程,可适用的典型问题有MAB,Q-learning,不过动作评价方程在MAB的应用之前已经用了大量的篇幅去分析讨论,这里就不再过多的赘述。本篇尝试用状态价值评价的方法来解决MAB问题,并以此为动态编程之例。
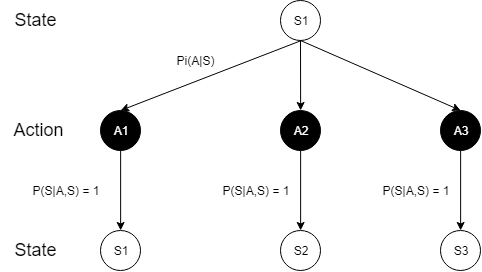
我们以一个3-lever的问题为例,画出它的State-Action-State树状图:
这里是以状态$ S_1 $为出发点,状态$ S_1 $表示第一个拉下第一个臂时的状态,以此类推。每一个动作所产生的状态都是确定的,所以这里的$ P(S_1 \to S_i) $就是$ \pi(A_i | S_1) $,$ S_1 $的状态评价方程可以写为:
$$ \mathbb{Value}(S_1) = \mathbb{Reward}(S_1) + \gamma \sum_{i = 1}^{3} \pi(A_i|S_1) \mathbb{Value}(S_i) $$
因为并不清楚每个状态所获得的具体的奖励,所以动作选择策略为随机选择,即每个动作被选择的概率为1/3。在动态编程中,每一次学习都需要将所有的状态遍历一遍,这样的好处是,即使$ \pi(A | S) $未知(随机选择策略),也可以保证每个状态的迭代次数对其最终结果的影响是相同的,得到的结果也是可靠的,这种收敛价值方程的方法被称为Policy Evaluation。注意动态编程在这里只是提供一个迭代求解状态价值评价的手段。对K-lever问题来说,动态编程将其分割为K个子问题分别求解更新对应的状态价值,这个过程是有违自然地强化学习的过程的,却可以提高求解效率。3-lever问题的状态评价迭代Matlab程序如下:
K = 3;
V = zeros(1, K);
Reward = [1 2 0.5];
P = zeros(1, K) + 1/K;
gamma = 0.5;
delta = 100;
%i = 1;
while(delta > 0.01)
delta = 0;
for state = 1:K
v = V(state);
V(state) = Reward(state) + sum(P.*gamma.*V); % Bellman equation
delta = max([delta abs(v - V(state))]);
end
%plot(i, delta, 'bo')
%hold on
%i = i + 1;
end
这里的$ Reward = [1\ \ 2\ \ 0.5] $,对应着每一个状态所得的奖励,$ \gamma $值为0.5,状态价值评价的最终结果为:
举个例子,依据这个状态价值评价矩阵来生成greedy-policy,那么无论当前处在什么状态,只要达到状态S2,就可以获得最优收益,所以greedy-policy的动作选择概率$P(A) = [0\ \ 1\ \ 0]$


 浙公网安备 33010602011771号
浙公网安备 33010602011771号