颜色空间系列2: RGB和CIELAB颜色空间的转换及优化算法

颜色空间系列代码下载链接：https://files.cnblogs.com/Imageshop/ImageInfo.rar （同文章同步更新）

在几个常用的颜色空间中，LAB颜色空间是除了RGB外，最常用的一种之一，不同于RGB色彩空间，Lab 颜色被设计来接近人类视觉。它致力于感知均匀性，它的 L 分量密切匹配人类亮度感知。因此可以被用来通过修改 a 和 b 分量的输色阶来做精确的颜色平衡，或使用 L 分量来调整亮度对比。这些变换在 RGB 或 CMYK 中是困难或不可能的，它们建模物理设备的输出，而不是人类视觉感知。

关于CIELAB颜色空间的更多原理说明，可见：http://en.wikipedia.org/wiki/Lab_color_space

本文研究的重点是RGB和LAB之间的快速转换过程。

首先，RGB和LAB之间没有直接的转换公式，其必须用通道XYZ颜色空间作为中间层，关于RGB和XYZ颜色空间的转换及优化，详见颜色空间系列1。

XYZ------>LAB转换公式如下：一般情况下我们认为Y_n,X_n,Z_n都为1。

$\begin{align} L^\star &= 116 f(Y/Y_n) - 16\\ a^\star &= 500 \left[f(X/X_n) - f(Y/Y_n)\right]\\ b^\star &= 200 \left[f(Y/Y_n) - f(Z/Z_n)\right] \end{align}$

其中

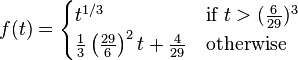
$f(t) = \begin{cases} t^{1/3} & \text{if } t > (\frac{6}{29})^3 \\ \frac13 \left( \frac{29}{6} \right)^2 t + \frac{4}{29} & \text{otherwise} \end{cases}$

在上述表达式中，X,Y,Z及t变量的取值范围都是[0,1]，对应的L分量的取值范围为[0,100],A和B分量都为[-127,127],因此，如果把L拉升至[0,255]，把A,B位移至于[0,255]，就可以同RGB颜色空间表达为同一个范围了。即使这样映射后，一般来说，LAB各分量的结果仍为浮点数，这个和RGB不同，但是在很多情况下，为了速度计效率，我们这需结果的取整部分，得到类似于RGB空间的布局。因此，对这类结果的优化更有实际意义。

关于这样的优化，OpenCv已经做了非常好的工作，各位看客也可以先看看OpenCv的代码，本文未直接沿用其优化，但本文的算法更简单明了，在保证结果无明显变化的同时，速度和效率都有30%以上的提升。

第一步，我们来看看f(t)这个函数的优化，f(t)是个分段函数，如果直接在函数体中判断，会多一些跳转和比较语句，不利于CPU的流水线工作，因此，我考虑的第一步是是否能用查表法来做。

在颜色空间系列1文章中，我们知道，转换后的XYZ值得范围是[0,255]，而这里的t值范围为[0,1],把if t>(6/29)^3这个算法映射到[0,255],则为 if t>2.26 ,因为XYZ都为整数，即此条件和if t>2等价，可见这里会出现一些漏判点；考虑2.26这个数字的特点，如果我们在把这个结果放大4倍，即XYZ范围为[0,1020],则判断条件随之升级为if t>9.04，取整if t>9，则漏判现象大为减少。这是提的第一点。

接着上面，这样的话我们就定义一个查找表，查找表大小应该和XYZ的域相同的，即上面的1020（我更喜欢1024），对于表中的元素值，为求速度，当然必须为int 类型，

也就是说，需要把计算出来的小数值放大一定倍数。这里不多说，见下面的代码：

    for (I = 0; I < 1024; I++)
    {
        if (I > Threshold)
            LabTab[I] = (int)(Math.Pow((float)I / 1020, 1.0F / 3) * (1 << Shift) + 0.5 );
        else
            LabTab[I] = (int)((29 * 29.0 * I / (6 * 6 * 3 * 1020) + 4.0 / 29) * (1 << Shift) + 0.5 );
    }

C#语言是强类型语言，一定要注意运算式中各变量的类型，比如上式中的1.0F/3,我常常写成1/3（这个的运算结果为0），结果往往是总觉得程序写得没问题，但运行效果就是不对，找半天BUG也找不到。

I / 1020的目的还是把值映射到[0,1]范围的。表达式最后的+0.5是因为(int)强制类型转换时向下取整的，+0.5则为四舍五入的效果。显然，这是我们需要的。

OK，有了这个查找表，下面的过程就简单了，对于A,B分量，就是进行简单的乘法、移位及加法，而对于L分量，必须有一个放大的过程，而这个过程我们应该直接从其系数入手，如下所示：

   const int ScaleLC = (int)(16 * 2.55 * (1 << Shift) + 0.5);
   const int ScaleLT = (int)(116 * 2.55 + 0.5);

2.55即为放大倍数，注意116这个数字，由于，其后的 f(x)已经进行了放大，该数字就不能再放大了。

通过以上分析，一个简单的而有高效转换算法就有了：

    public static unsafe void ToLAB(byte* From, byte* To, int Length = 1)
    {
        if (Length < 1) return;
        byte* End = From + Length * 3;
        int X, Y, Z, L, A, B;
        byte Red, Green, Blue;
        while (From != End)
        {
            Blue = *From; Green = *(From + 1); Red = *(From + 2);
            X = (Blue * LABXBI + Green * LABXGI + Red * LABXRI + HalfShiftValue) >> (Shift - 2);　　//RGB->XYZ放大四倍后的结果
            Y = (Blue * LABYBI + Green * LABYGI + Red * LABYRI + HalfShiftValue) >> (Shift - 2);
            Z = (Blue * LABZBI + Green * LABZGI + Red * LABZRI + HalfShiftValue) >> (Shift - 2);
            X = LabTab[X];　　　　　　　　　　// 进行查表
            Y = LabTab[Y];
            Z = LabTab[Z];
            L = ((ScaleLT * Y - ScaleLC + HalfShiftValue) >>Shift);
            A = ((500 * (X - Y) + HalfShiftValue) >> Shift) + 128;
            B = ((200 * (Y - Z) + HalfShiftValue) >> Shift) + 128;
            *To = (byte)L;          // 不要把直接计算的代码放在这里，会降低速度
            *(To + 1) = (byte)A;    // 无需判断是否存在溢出，因为测试过整个RGB空间的所有颜色值，无颜色存在溢出
            *(To + 2) = (byte)B;
            From += 3;
            To += 3;
        }
    }

再来看看反转的过程，即LAB-XYZ的算法，理论公式如下：

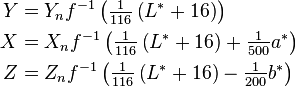
$\begin{align} Y &= Y_n f^{-1}\left(\tfrac{1}{116}\left(L^*+16\right)\right)\\ X &= X_n f^{-1}\left(\tfrac{1}{116}\left(L^*+16\right) + \tfrac{1}{500}a^*\right)\\ Z &= Z_n f^{-1}\left(\tfrac{1}{116}\left(L^*+16\right) - \tfrac{1}{200}b^*\right)\\ \end{align}$

其中：

$f^{-1}(t) = \begin{cases} t^3 & \text{if } t > \tfrac{6}{29} \\ 3\left(\tfrac{6}{29}\right)^2\left(t - \tfrac{4}{29}\right) & \text{otherwise} \end{cases}$

注意，我这里说的转换有个前期条件，即LAB的数据是用类似于RGB空间的布局表达的，也就是说LAB各元素为byte类型。

我曾自己的研究过这些算法，如果完全像上面那样靠整数乘法及移位来实现，主要的难度是t^3这个表达式的计算结果会超出int类型的表达范围，而如果用64位的long类型，在目前32位机器依旧占主流配置的情况下，速度会下降很多。因此，我最后的研究还是以空间换时间的方法来实现。具体分析如下：

观察上式分析，Y的值只于L有关，而L由于我们的限定，只能取[0,255]这256个值，因此建立一个256个元素的查找表即可，而X及Z的值分别于L及A/B有关，需要建立256*256个元素的查找表即可，大约占用0.25MB的内存。查找表的建立如下：

for (I = 0; I < 256; I++)
    {
        T = I * Div116 + Add16;
        if (T > ThresoldF)
            Y = T * T * T;
        else
            Y = MulT * (T - Sub4Div29);
        TabY[I] = (int)(Y * 255 + 0.5);　　　　　　// 映射到[0,255]
        for (J = 0; J < 256; J++)
        {
            X = T + Div500 * (J - 128);
            if (X > ThresoldF)
                X = X * X * X;
            else
                X = MulT * (X - Sub4Div29);
            TabX[Index] = (int)(X * 255 + 0.5);

            Z = T - Div200 * (J - 128);
            if (Z > ThresoldF)
                Z = Z * Z * Z;
            else
                Z = MulT * (Z - Sub4Div29);
            TabZ[Index] = (int)(Z * 255 + 0.5);
            Index++;
        }
    }

最终的LAB-RGB转换算法如下：

 public static unsafe void ToRGB(byte* From, byte* To, int Length = 1)
    {
        if (Length < 1) return;
        byte* End = From + Length * 3;
        int L, A, B, X, Y, Z;
        int Blue, Green, Red;
        while (From != End)
        {
            L = *(From); A = *(From + 1); B = *(From + 2);
            X = TabX[L * 256 + A];      // *256编译后会自动优化为移位的
            Y = TabY[L];
            Z = TabZ[L * 256 + B];
            Blue = (X * LABBXI + Y * LABBYI + Z * LABBZI + HalfShiftValue) >> Shift;　　
            Green = (X * LABGXI + Y * LABGYI + Z * LABGZI + HalfShiftValue) >> Shift;
            Red = (X * LABRXI + Y * LABRYI + Z * LABRZI + HalfShiftValue) >> Shift;
            if (Red > 255) Red = 255; else if (Red < 0) Red = 0;
            if (Green > 255) Green = 255; else if (Green < 0) Green = 0;            // 需要有这个判断
            if (Blue > 255) Blue = 255; else if (Blue < 0) Blue = 0;
            *(To) = (byte)Blue;
            *(To + 1) = (byte)Green;
            *(To + 2) = (byte)Red;
            From += 3;
            To += 3;
        }
    }

通过以上的分析，可以看出，这个转换的过程代码很简单，清晰，而且效率不菲,对一副4000*3000的数码照片进行RGB->LAB,然后再LAB->RGB算法本体的时间只有250ms。

还有几个优化的地方就是我的所有的查找表都不是用的C#的数组，而是直接分配内存，这是因为C#的数组在很多情况下会有一个判断是否越界的汇编码，而用非托管内存则不会。

比如，以下是用非托管内存的数组访问的反汇编：

  static int* TabX = (int*)Marshal.AllocHGlobal(256 * 256 * 4);    // 这是原始的定义

                X = TabX[L * 256 + A];      // *256编译后会自动优化为移位的
00000037  mov         eax,edi 
00000039  shl         eax,8 　　　　　　　　　// 看到这里的移位没有
0000003c  add         eax,edx 
0000003e  mov         edx,dword ptr ds:[005A1F0Ch] 
00000044  mov         eax,dword ptr [edx+eax*4] 
00000047  mov         dword ptr [ebp-14h],eax

而用C#的数组方式生产的汇编如下：

static int[] TabX = new int[256 * 256];     // 这是原始的定义

                X = TabX[L * 256 + A];      // *256编译后会自动优化为移位的
0000003c  mov         eax,edi 
0000003e  shl         eax,8 
00000041  add         eax,edx 
00000043  mov         edx,dword ptr ds:[02A27C68h] 　　
00000049  cmp         eax,dword ptr [edx+4] 　　// 多出这两句代码
0000004c  jae         00000133 
00000052  mov         eax,dword ptr [edx+eax*4+8] 
00000056  mov         dword ptr [ebp-14h],eax

其实还有很多细节上的优化的东西，比如语句的顺序的讲究，有的时候就是调换下不同行的语句，程序的执行效率就有很多的不同，这主要是编译器的优化不同造成的，比如适当的顺序会让编译器选择某个常用变量为寄存器变量。还比如有人喜欢用下面的代码

  *To++ = (byte)L;
  *To++ = (byte)A;
  *To++ = (byte)B;

来代替：

 *To = (byte)L;          
 *(To + 1) = (byte)A;    
 *(To + 2) = (byte)B;
 To += 3;

虽然代码看上去简洁了，可你执行后就知道速度反而慢了，为什么，我想我会在适当时候写一些关于C#优化方面的粗浅文章在对此进行解释吧。

最后附上一些处理的效果，还是拿系列1文章中那些崇洋的新贵门来做实验吧：

原图：

转换后的综合图像：

L通道：

A通道：

B通道：

同样的道理，上述快速算法如果进行多次转换，必然也存在精度上的损失。

LAB空间在以后的肤色检测文章中还会有提到。

'*********************************************************************

　　转载请保留以下信息：

　　作者： laviewpbt

　　时间：2013.2.2 11点于家中

　　QQ:33184777

　　E-Mail : laviewpbt@sina.com

posted @ 2013-02-02 11:41 Imageshop 阅读(22560) 评论(4) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

颜色空间系列2: RGB和CIELAB颜色空间的转换及优化算法

公告