点分治选讲

1. AT_cf17_final_j Tree MST

\(Lemma.\) 对于一个图 \(G = (V,E)\)，我们将 \(E\) 分成 \(E_1,E_2,...,E_n\)，其中 \(E_i\) 是 \(E\) 的一个划分。那么我们对每个 \(E_i\) 求 MST 得到 \(E_1',E_2',...,E_n'\)，再把这些边作为求 MST 的对象跑 MST，得出的就是原图的最小生成树。

\(Proof.\) 我们发现原定理等价于，对于原图上 MST 的一条边 \((u,v)\)，其必然在其子边集 MST 的一条边上。

我们找到包含边 \((u,v)\) 的子边集 \(E_j\)，考虑反证。设 \((u,v)\in E_j\) 且 \((u,v)\notin E_j'\)。

那么在 \(E_j\) 中必然存在一条 \(u\) 到 \(v\) 的路径 \(\mu\) 使得 \(\sum_{e\in \mu} w_e\leq w(u,v)\)。为了后面的论述方便，我们取最大边权最小的路径 \(\mu\)（即 \(\mu\) 是在子边集中第一条让 \(u\) 和 \(v\) 连通的路径）。那么显然的，\(\mu\) 的最大边权一定小于等于 \(w(u,v)\)，不然在跑 Kruskal 的过程中，一定会先连到 \((u,v)\)，这与 \(\mu\) 的最优性矛盾。

根据我们上面的论述，我们得到了 \(\forall e\in \mu\)，\(w_e\leq w(u,v)\)。而在原图跑 MST 的过程中，在 \((u,v)\) 加入之前，\(\mu\) 中所有的边都已经被加入。这时 \(u\) 和 \(v\) 连通，根据 Kruskal 算法，\((u,v)\) 边不可能再被加入。此时 \((u,v)\notin E'\)，这与我们假设的 \((u,v)\in E'\) 矛盾。

证毕。

下面我们根据这个东西想。我们不妨把式子拆开，\(w_u+w_v+dist(u,v)=(w_u+depth_u)+(w_v+depth_v)\)，我们可以发现我们拆的特别好看，把 \(u\) 和 \(v\) 基本分开了。但是我们不定根就完蛋了，因为还得减去两倍 \(depth_{lca}\)。所以我们考虑在根处统计贡献。但是在根处统计它依然是 \(O(n^2)\) 的。于是我们可以往点分治上想（笔者认为这是非常自然的），或者说你也可以认为他是个路径问题然后往这个方面想。

注意一下我们的本质是什么，其实就是尽量的缩减有效边数。而我们缩减的方法就恰好需要使用到上面的定理和点分治的结构。我们先感性的想一下这个算法：对于一个根 \(u\)，我们强制让路径经过这个根，那么我们肯定是找到 \(w_u+depth_u\) 最小的点与其他点配对，对于每一个根都这么办。最后把这些边提出来跑一遍 MST。但是正确性在哪里呢？我们可以从定理出发研究这个问题。

我们把刚才的过程用定理的方式描述一遍：即对于每一个根 \(u\)，我们把过 \(u\) 的路径划分出一个集合。剩下的我们先不管，再剩下的点分治过程我们继续对剩下的集合进行划分，最后划分出了 \(m\) 个集合。对于每一个集合，他的 MST 求解方式如上所说（因为是完全图 MST 所以可以这么干）。

现在我们求出了 \(m\) 个集合中 MST 的边，接下来我们再跑 MST 显然就可以得出原图 MST 了。于是正确性我们也说明完毕了。

2. QOJ4815. Flower's Land

难点并不在于点分治的一道点分治题。

首先我们可以很容易的发现，题目要求我们买一个联通块。根据我们多年做 Shoppings 的经验，你可以把联通块分成过分治中心和不过分治中心两种。这样你可以点分治维护联通块，并且要求必选根，这样很好处理。

顺便说一下题目转化为：对于每个点 \(u\)，求出包含其的大小为 \(k\) 的最大权值联通块。

其实你要是求最大权值联通块就好做了，这个东西它认为强制了一个限制叫包含 \(u\)，然后你就完蛋了。因为对于这个分治中心，你需要强制选 \(u\) 到 \(rt\) 这条到根链，而不能跳过子树，这很困难。

于是你考虑怎么把到根链排除掉，这个非常困难，然后你就可以把两个背包合并起来再加上强制选的即可。这个东西涉及到一个 Trick：树上到根链的补，我把代码放到这里，你最好感性理解且理解透彻，毕竟是非常巧妙的。

点击查看代码

void DFSSiz(LL u, LL fa)
{
	Siz[u] = 1; dfn[u] = (++ dfsTime); idf[dfsTime] = u; rdfn[u] = rdfsTime + 1; 
	for(LL i = 0; i < G[u].size(); i ++)
	{
		LL v = G[u][i]; if(v == fa || vis[v]) continue;
		DFSSiz(v, u); Siz[u] += Siz[v];
	}
	idg[++ rdfsTime] = u;
	return;
}
void DFSCalc(LL u, LL fa, LL depth, LL Sum)
{
	LL nd = k - depth;
	for(LL i = 0; i <= nd; i ++) ans[u] = max(ans[u], f[dfn[u] + 1][nd - i] + g[rdfn[u] - 1][i] + Sum);
	for(LL i = 0; i < G[u].size(); i ++)
	{
		LL v = G[u][i]; if(v == fa || vis[v]) continue;
		DFSCalc(v, u, depth + 1, Sum + A[v]);
	}
	return;
}

3. CF566C Logistical Questions

用我的理解稍微证明一下这种东西。我们先不妨假设我们的答案根是一个点而不是一条边（边是可以推广的，并且很简单），我们要证明的是这么一个图。

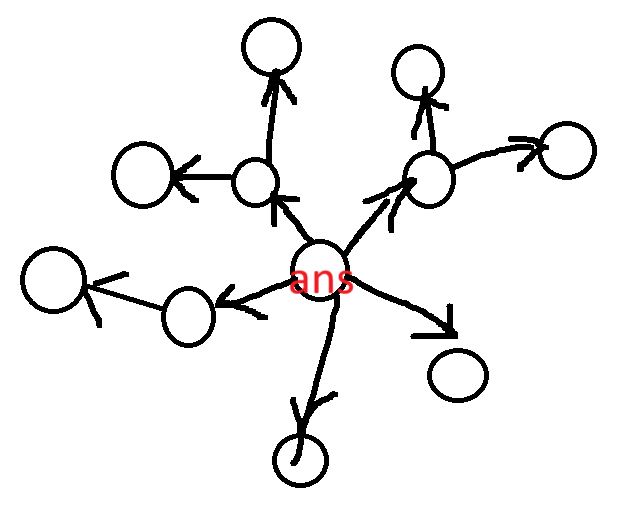
即要证明的是在我答案在点上的情况下，有且仅有一个点是答案的谷点，且其他点的答案从谷点向上单调不减（即树上凸性）。

我们先说明这样的性质有什么好处：好处是我们可以任意选一个点然后进行调整，由于树的凸性，我们最多只会向一个子树内进行调整（从上图可知）。而且我们有方法快速计算调整到哪个子树，这种计算方法与我们的证明大同小异，下面会说。于是我们可以通过调整法找到这个子树。

而这种东西我们根据快递员 Trick 很容易想到每次选取子树重心进行调整。这样我们只会调整 \(\log n\) 次，这就给我们的答案计算留下了很大的时间。

常见错误调整一则：选取子树内的分治中心，求以这些分治中心为根的最小答案，并向此分治中心移动。这种方法在大多数情况下是对的，但有一定概率错误。

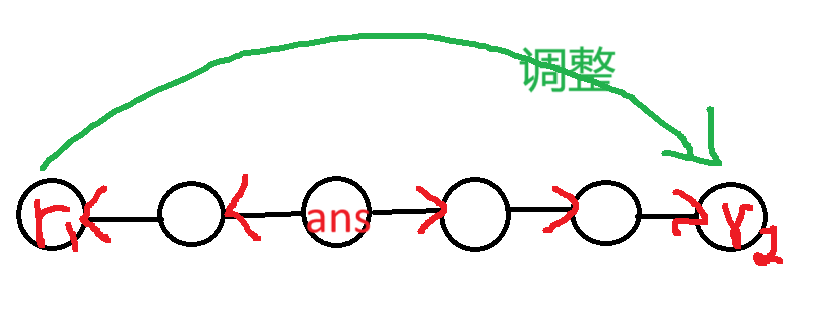
比如这样就有一定概率完蛋。

那么我们先说正确调整的方法，我们看到错误方法错误的原因是其跨过了答案谷点，那么规避的方法也非常简单，即对于我们现在的分治中心 \(u\)，向每个子树方向取一段极小的 \(\Delta x\)，看一下改变量即可。那么改变量其实就是导函数，我们对原函数求导，即 \(f'(x)=1.5wx^{\frac{1}{2}}(x\geq 0)\)，我们设此点有 \(k\) 个子树，\(p_i(i\in [1,k])\) 代表了第 \(k\) 个子树内的改变量之和。那么根据我们上面的结论，找到 \((\sum_{i=1}^k p_i) - 2p_j < 0\) 的第 \(j\) 棵子树继续进行分治即可。

接下来我们说一下证明：比如我们现在随机选一个点 \(u\)，任选其一个子树 \(j\) 计算 \((\sum_{i=1}^k p_i) - 2p_u\)，若其大于 \(0\)，那么我们向这个方向走的第一个点的答案就会大于它，我们现在挪动到这个点上，由于 \(\forall i\) 满足 \(f'(i)\geq 0\)，于是我们记挪动到的这个点为 \(v\)，有 \(p_u>p_v\)，于是 \((\sum_{i=1}^{k'} p_i) - 2p_v\) 只会增大不会减小，再向这个方向挪动也是一样。我们可以归纳说明这个是对的。

接下来，如果我们不幸选到了那个会让答案变小的子树 \(s\)，那么由于我们上面证明了越往这个方向挪，\(p\) 值就会越小，即整个的改变量在增大，所以这个东西早晚会变成正的的情况，而我们的正负分界点就是我们的答案。

接下来证明不会有两个谷点（在答案为点的情况下），这个非常好理解，我们任意选一个谷点 \(u\) 进行调整，往外发散一定变大，所以另一个"谷点"的值一定小于 \(u\)，这与谷点的定义矛盾，证毕。

然后我们就做完了。

4. P9058 [Ynoi2004] rpmtdq

首先我们可以发现，如果我们把区间左端点挂 \(x\) 轴上，区间右端点挂 \(y\) 轴上，那么我们的区间就可以看做一个点，然后询问的是一个 \(4-side\) 矩形的点权最小值。进一步可以发现，由于有 \(i\leq j\) 这个限制，于是我们只需要限制 \(i\geq l\) 和 \(j\leq r\)，于是变成了 \(2-side\)，从右往左扫描线，维护前缀最小值，树状数组即可。

这个做法的缺点很明显，就是点达到了 \(O(n^2)\) 的级别，于是我们要干的事也非常明了，减少点的数量。

我们怎么减少点的数量？一种非常经典的套路就是使用支配点对，即我们考虑若区间 \(i\) 把区间 \(j\) 严格偏序了，那么 \(j\) 就是无用点，接下来我们证明有用点（支配点对）的个数仅为 \(O(n\log n)\) 级别。

题目给定的是树，于是我们考虑把 \(dist(i,j)\) 拆掉，拆成 \(dist(i,rt)+dist(rt,j)\)，树上到根路径拼起来这件事让我们联想到点分治。对于一个分治中心 \(rt\)，我们把联通块内 \(dist(rt,i)\) 都搜出来，从小到大排个序，我们选取两个点 \(i,j\) 不防设 \(i\) 在 \(j\) 前面，那么我们要证明，\((i,j)\) 能构成支配对的必要条件是 \(i\) 是 \(j\) 在编号上的前驱或者编号上的后继（在 \(dist(rt,i)\leq dist(rt,j)\) 的前提下）

考虑反证法证明：若存在 \(g<pre_j\) 且 \((g,j)\) 构成支配对。

则 \(dist(g,pre_j)=dist(g,rt)+dist(pre_j,rt)\leq dist(j,rt)+dist(g,rt)=dist(j,g)\)

由于 \(len([g,pre_j])<len([g,j])\)，且 \(dist(g,pre_j)\leq dist(g,j)\) 所以 \((g,j)\) 被 \((g,pre_j)\) 支配了。证毕。

于是总共点分治的过程中只会提供 \(n\log n\) 级别的点对，于是我们就可以扫描线了。

时间复杂度 \(n\) 带 \(1\) 或 \(2\) 只 \(\log\)，\(q\) 带 \(1\) 到 \(2\) 只 \(\log\)。看实现是否精细，不精细的话需要大力卡常。

5. P7215 [JOISC 2020] 首都

点分治维护连通块的方法。不是难题。

首先你要注意到你选的是一个连通块，又是一棵树，很难不想到点分治对吧。点分治的好处在于可以强制选择分治中心，我们把当前分分治中心所代表的颜色的所有点都加入队列跑多元 BFS。多元 BFS 的跑法就是以当前分治中心为根跳父亲，当你遇到另一个点且这个颜色你没有选过的时候就把所有这个颜色的点都加入队列，直到形成连通块为止。这样你选的点的个数一定是最小的。

注意，如果扩展到的颜色中有任何一个不在当前连通块内，直接结束，因为一定会跨过你点分树上的父亲，这样一定不优。即使统计也是会在以父亲为根统计到。

然后就做完了。

6. BZOJ 3648 寝室管理

非常直观的思路。最开始唐了。

首先第一问的树上大于等于 \(k\) 的路径条数。借这个题我们讲一下理论做法的实现方式。

首先是第一种非容斥的做法，这种就是这样：

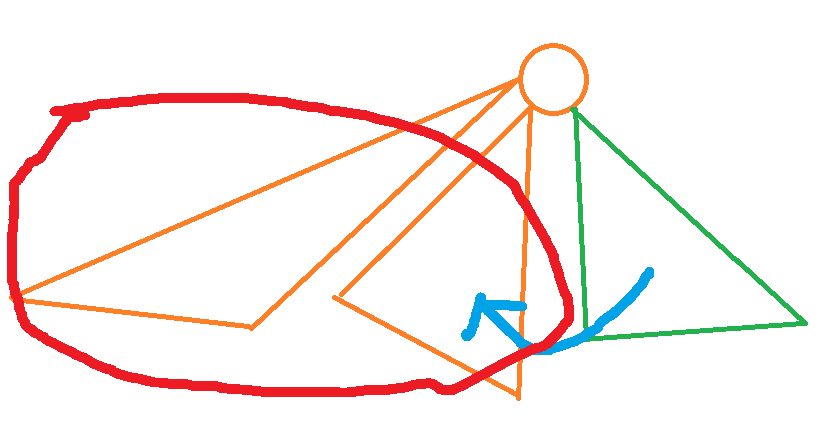
一目了然（雾）

反正就跟 Combining Subtree 挺像的，就是我们把前面的距离都暴力插进了树状数组，然后我们强制钦定路径有一端在我们的绿子树里面，然后和树状数组里面（橙子树部分）的一半路径拼起来。实现上，我们可以暴力枚举绿子树的每一条到分治中心的路径，假设其长度为 \(l\)，那么我们就在 BIT 里查长度为 \(k-l\) 到 INF 的路径。最后再把绿子树的答案全部插入 BIT 里。 显然的，这种方法是不可能重复计数的。

然后是一种容斥做法。

一目了然（雾）

即我们先随便选，我们暴力遍历把所有路径全都插进去，每次插的时候直接查。接下来，我们把 BIT 清空。遍历每个小分治子树，然后对每个小分治子树再进行这个操作，然后减去掉不合法的即可。

这两种做法是基本等价的。

Bonus：你可以联想一下这两种做法与某个数学公式其实是息息相关的。

接下来我们考虑基环树上的问题，这个其实也不是很简单。

如果你稍微见过一个基环树问题的话，你就会很容易想到思路。我们先把环直接断掉，在树上跑一边树分治，我们再想办法把这条边加上。很显然，我们算的是：强制经过本边的长度大于等于 \(k\) 的路径条数。

我们假设这条边的两端为 \(cutu\) 和 \(cutv\)。我们以 \(cutu\) 为根扫一遍整棵树，这样我们可以得到一个所有点到 \(cutu\) 的距离值，方便我们后续的操作，具体我们要做的可以描述为下面这个图。

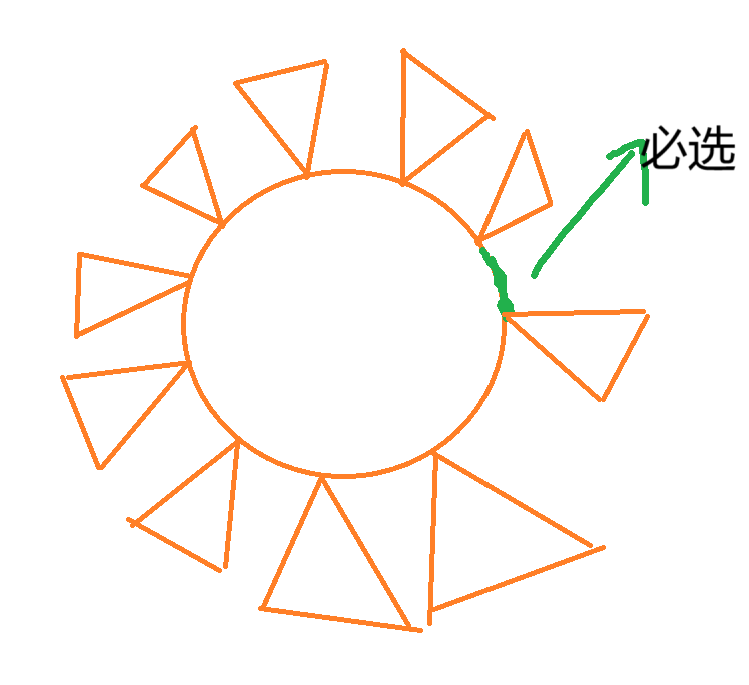
草我到底在画什么啊（）

绿色的边在我们真正建的时候可以断开。我们从 \(cutv\) 开始做。首先把所有路径长度信息全部插入 BIT 中。我们把环找出来，按序遍历环上的每个点，每次先把其对应的子树删掉（橙色三角），暴力遍历，然后作为路径的一半去匹配插入树状数组的路径。所以整个过程看起来就莫名的反着来，但是还是很直观的，然后就做完了。

7. AT_agc001_c [AGC001C] Shorten Diameter（HDU6881） 要求复杂度 \(O(n\log⁡n)\)

最简单的一个题。我们只考虑 \(k\) 是偶数的情况，\(k\) 是奇数随便变一下就好了。

那么题目等价于：选取一个根，使得距离其小于等于 \(\frac{k}{2}\) 的点数最多。这个转化是非常显然的。

嗯然后你的目的是利用点分治对于每个根求出我们想求的东西。这个是点分治对单点进行贡献的套路。

能对 \(u\) 点进行贡献的只有 \(u\) 点的点分树到根链。按照子树顺序正着扫一遍，反着扫一遍，或者你使用容斥大法会更加直观。然后就做完了。

8. P4115 Qtree4

点分树题。首先我们证明点分树上的一个经典结论：有两点 \(u\) 和 \(v\)，记它们在原树上的 LCA 为 \(lca\)，点分树上的 LCA 为 \(lca'\)，则 \(dist(u,lca)+dist(lca,v)=dist(u,lca')+dist(lca',v)=dist(u,v)\)。

\(Proof.\) 首先我们要知道 \(dist(u,k)+dist(k,v)=dist(u,v)\) 在树上的充分必要条件是 \(k\) 在 \(u\) 到 \(v\) 的路径上，但这并不能证明 \(lca'\) 的结论。

我们继续寻找 \(k\) 在 \(u\) 和 \(v\) 路径上的等价条件。我们可以发现，其等价于：删去 \(k\) 后，\(u\) 和 \(v\) 不连通。也就是使得 \(dist(u,k)+dist(k,v)=dist(u,v)\) 的集合 \(K\) 是删去后使得 \(u\) 和 \(v\) 不连通的点的集合。

根据点分树的定义，\(lca'\) 的作用是把该分治中心划分成若干个连通块。于是 \(lca'\) 不同子树必然不连通，也就是删去 \(lca'\) 后，\(u\) 和 \(v\) 不连通。证毕。

这个定理在后面求距离时能让你想清楚求法的正确性。

根据点分树维护信息的经典套路，我们应该往 \(u\) 分治子树内到 \(u\) 的答案和 \(u\) 分治子树内到 \(u\) 在点分树上的父亲的某些答案进行维护。这样做有时是为了方便容斥，有时是为了方便父子关系之间的递推。

我们记 \(f_u\) 为 \(u\) 分治子树内到 \(u\) 在点分树上的父亲的距离集合（我们后面要选取最大值所以这个至少要开成一个堆），\(g_u\) 为 \(u\) 在每个小分治子树里选一条最大路径的集合（开成堆），\(h\) 为每个分治中心贡献答案的集合（也是堆）

有了这些东西，我们可以很容易的由祖先后代的递推关系得出所有的堆，这样我们就会做不带改的了。接下来我们建出点分树，每次白变黑就是删除一个点，其只对自己到最上面的分治根这条链上的点有用，由点分树的结构，其只会修改 \(\log\) 个节点，每个节点的维护更新三个堆也是 \(\log\) 的，这是可以接受的。

实现看自己喜好，可以选用 set 套 pair，multiset，堆等多种方式实现，正确性都没有问题常数有差异（差异还不小），选错就卡常。

9. QOJ5357. 芒果冰加了空气

很好的刻画计数题。

首先如果你对点分树较为熟悉，那么很容易发现：一棵树 \(T\) 的点分治方案与点分树构成双射（一一对应），于是我们把问题转化为了对原树的点分树计数。

转移较为难想。但是你考虑一下我们要干什么，我们肯定不想给自己找麻烦，于是我们想的是在原树上做这个事。数学方法我没有想出来于是我们考虑在树上 dp。

考虑 Combining Subtree 的过程，我们把以 \(v\) 为根的子树并到了 \(u\) 上面。这时，我们连接了在 原树 上 \((u,v)\) 这条边。我们从表象来看合并了两棵树，但是从你计数的手法来看，我们其实是想合并两棵点分树的。接下来考虑怎么合并。看图：

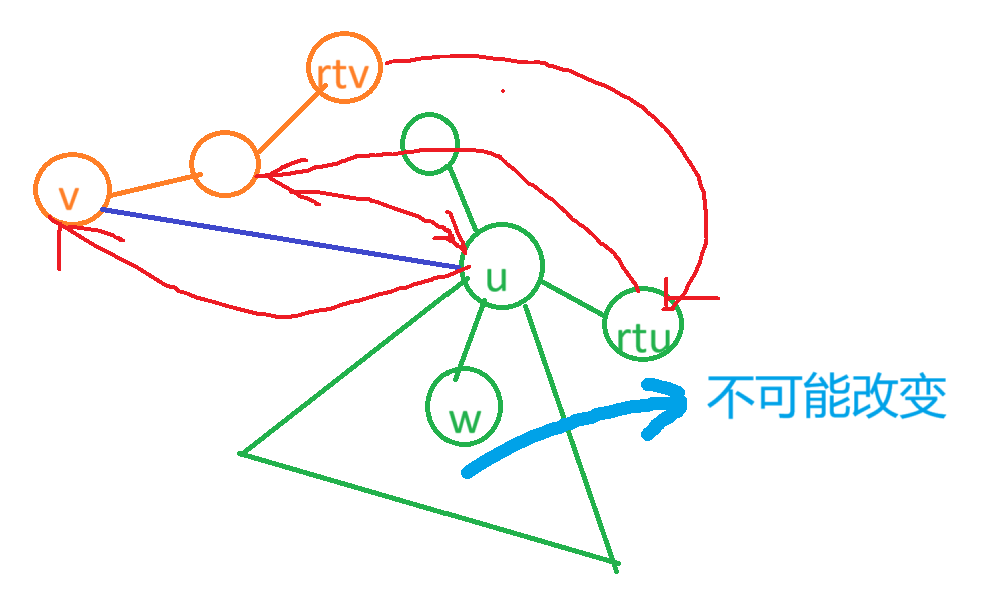
比较抽象，我们一部分一部分解释。类似于 FHQ-Treap 的 Merge 过程，首先树的合并本身你是要有点儿素质的，合并过程中其祖先后代关系必然不可能改变。

这给我们了两个信息：

1. 形如 \(w\) 这样由于和 \(v\) 根本不在一个连通块内的点，其绝对位置可能改变，但其相对位置一定是不变的。于是我们得出改的只有 \(u\) 到 \(rtu\) 这条点分树到根链和 \(v\) 到 \(rtv\) 这条链。

2. 由于祖先后代关系不能改变，所以是两个有序链互相插入，即两个有序序列合并的方案数，即 \(\binom{n+m}{n}\)。

那么我们就可以设计出状态了。我们需要知道 \(n\) 和 \(m\) 即 \(u\) 和 \(v\) 在未合并时点分树的深度，合并后，由于我们钦定了 \(u\) 是 \(v\) 的父亲，所以我们把 \(v\) 的信息传递到 \(u\) 上。\(u\) 在新点分树上的深度可能是 \(n\) 到 \(n+m\) 之间的任意数。由于编号是连续的所以我们可以后缀和优化 dp 进行转移，乘上面的组合系数就可以完成类树上背包的转移了。

10. CF2101E Kia Bakes a Cake

很套路也很好的题，一道点分治优化距离类型 dp 的题目。思路顺水推舟，每一步都非常自然。

权值是有上界的，即 \(w\leq n\)。又由边权每次乘以 \(2\)，很难不让人联想到 \(\log\) 之类的东西，随便分析一下，设 \(w(v_1,v_2)=p\)，则 \(w(v_{m-1},v_m)_{min}=p\times 2^{m-1}\)，令 \(p=1\) 即可得到长度的上界，即 \(2^{m-1}\leq n\)，两边同时 \(\log_2\)，得到 \(m\leq [\log_2 n] + 1\)。

这么好的性质很难让我们不把它记到状态里。设 \(f_{st,len,u}\) 表示起点在 \(st\)，目前在 \(u\) 点，已经走过了 \(len\) 个点的最后一条边的最小值，这个转移看起来是简单的我们先不管它。那么现在看起来题目把我们引领到了一个很像 dp 的区域里。那我们顺着走，证明 dp 是可行的（即 dp 没有后效性）。证明分为两步：

1. \(len\) 这一维的无后效性，这个如果你先枚举 \(u\) 这一维确实是会有后效性的，因为你并没有保证你的前置状态一定被更新了，而且你根本不知道转移的顺序。但是如果你会线段树优化 dp 你是很容易知道可以把 \(len\) 这一维第一个枚举的，这样一层转移完才会进行下一层，这样没有后效性。

2. \(u\) 这一维的无后效性，即证明我们的 dp 不会出现不合法的情况，那这个就需要看一下原题的描述了。我们假设在那个完全无向加权图上，dp 过程中 \(x\) 被重复走了两次，假设 \(x\) 的前置点是 \(y\)，由于路径每次乘 \(2\)，根据等比数列求和公式 \(w(x,y)>w(x,g_1)+w(g_1,g_2)+...+w(g_t,y)\)，而 \(w(x,y)\) 是树上 \(x\) 到 \(y\) 中最短的唯一路径，此不等式与题目所给的树形结构 \(T\) 相矛盾，证毕。

那么我们现在起码有了一个多项式复杂度的 dp 做法了。我们套路的考虑从两部分优化它。

1. 状态定义：注意到我们的状态内部非常不和谐的记录了一个 \(st\)，这是因为我们必须要知道最后把答案贡献给谁，那么这个很讨厌。但是你考虑到我们现在知道什么，我们同时知道了起点和终点！，这并不是我们想要的，因为我们知道的太多了，我们并没想知道终点是啥。由路径的对称性，我们只要反着跑，限制后面的长度至少是前面的一般就好了，这样我们的 \(u\) 维就能记录最后的 \(st\)，不用单独记了，我们现在也只能知道起点了，这非常好。

2. 状态转移：原来的是 \(f_{len,v}=w(u,v)(w(u,v)\leq [\frac{f_{len-1,u}}{2}])\)。这是树上距离，与原树的祖先后代关系无关，而且这是原树的路径，转移我想知道树上所有路径的信息，且还是给单点进行贡献，这与点分治完美契合，于是我们使用点分治优化这个转移，由于限制是 1-side 的，我们完全可以使用 BIT 维护极值。然后跑 \(\log\) 次点分治按层转移即可。

然后我们就做完了，时间复杂度 \(O(n\log^3 n)\)。