Atcoder Regular Contest 168 题解

[ARC168C] Swap Characters

稍微有点儿困难，先摘一张题解里的图。

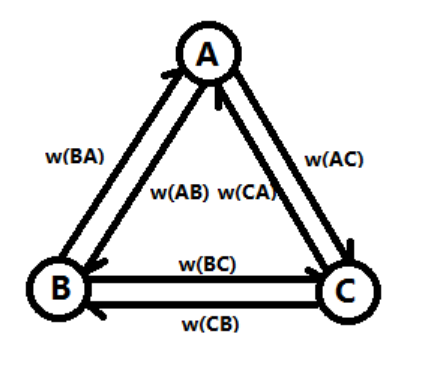
其实就是一个置换的问题。对于把原串 \(s\) 置换到 \(t\)，我们可以拆成把 A 换到 C 的地方，把 A 换到 B 的地方，把 B 换到 C 的地方，反之亦然（如图）。根据贪心的策略，我们一定是使用最少的步数将两个串变相同，这样我们的计数才有正确性。

我们先考虑我们到底是怎样把 \(s\) 置换到 \(t\) 的。这非常简单，首先 A 到 B 和 B 到 A 是对称的，我们可以把这两个同时减去 \(1\)，其他两组是一样的（我们把这样的操作称作操作 \(1\)）。经过操作 \(1\) 后，如果 \(s\) 可以变到 \(t\)，那么一定会形成一个边权相同的环或者全部消没。

如果是一个边权相同的环，我们采用另一种策略，如把 ABC 换为 BCA（当然还存在另一种置换方式，这两种都要考虑），就把 A 和 B 交换，A 和 C 再交换，使用 \(2\) 次操作将环的权值减去 \(1\)。想清楚这个事情后，我们的计数就变得简单了起来。

首先我们当然可以把 \(6\) 条边的权值都枚举一遍，但是复杂度过高。但是根据上面的贪心策略，我们应当有一个发现，就是边权相同的环这个限制非常死，如若我们现在考虑的是 ABC 换为 BCA 的置换，且如果我枚举了这个置换的个数，且我知道了 \(w(AB),w(BC),w(CA)\)，那么另一边的权值是固定死的！换句话说，我们实际上仅有四个自由元！

于是我们可以考虑枚举这四个自由元的个数。然后考虑在一个序列里，以 A 进行变换为例，看他是进行 AB 变换，还是 AC 变换，还是轮环置换，因为如若两个位置置换方式相同，他们没有区别，于是这实际上是一个多重集组合数问题，于是我们就做完了！把三个字符一共九种变换使用多重集组合数组合起来就好了！

[ARC168D] Maximize Update

区间 DP 唐诗题。难度在于二维前缀和。

首先 \(n\leq 500\) 一眼区间 DP，或者你随便试试也知道根本不可能做线性的 dp，你状态都定义不了，你还得在前缀中挖掉一个东西，你也不知道挖的什么东西。

然后套路的定义 \(f_{i,j}\) 表示区间 \([i,j]\) 已经染完颜色的能染色的最多次数。显然的，对于一个大区间 \([i,j]\)，选取一个中间点 \(k\)，从 \(f_{i,k}+f_{k+1,j}\) 转移是可行的。

观察到显然的性质，对于一个区间 \([i,j]\)，如果存在位置 \(k\) 在区间 \((i,j)\) 内，且 \(k\) 未被上色，我们就可以选取一个左端点在 \([i,k-1]\) 且右端点在 \([k+1,j]\) 中的区间进行染色，此时答案加一。因为我们保证了最开始序列无色，所以我们选取 \(f_{i,k-1}\) 和 \(f_{k+1,j}\) 时 \(k\) 一定无色，这保证了这个 dp 的无后效性。

于是我们的问题变为，是否能找到一个区间使得其左端点在 \([i,k-1]\) 且右端点在 \([k+1,j]\) 中。考虑区间平面经典转化，将左端点设为 \(x\) 坐标，右端点设为 \(y\) 坐标，此时问题变为二维数点问题，由于范围不大，直接做二维前缀和查询即可。

[ARC168E] Subsegments with Large Sums

经典题，看到划分成恰好 \(k\) 段，第一考虑将段数记在 dp 状态内进行转移，对于此题来说复杂度过高，第二套路的思考 wqs 二分（带权二分）进行处理。

考虑到由于直接 wqs 二分其答案没有单调性也没有凸性。

于是考虑经典策略，二分答案，我们二分段数，看是否能够 check 成功。考虑如何刻画成功这一性质，非常简单，我们给每个选的段 \([l_i,r_i]\) 赋权为 \(V_i=r_i-l_i\)，其充要条件为 \(\sum V_i \leq n-k\)。此时，选的段数 \(x\) 和 \(g(x)\) 构成的点集 \((x,g(x))\) 是有凸性的，并且我认为是有单调性的。感性理解，首先单调性是不难证明的，凸性就是肯定先选段长小的，后面没办法了才选段长大的。于是这个函数是一个下凸函数。

考虑 wqs 二分如何实现。我们二分斜率 \(k\) 来切 \((x,g(x))\)。具体来说，由于 \(g(x)=kx+h(x)\)，则 \(h(x)=g(x)-kx\)。于是根据经典套路，我们 dp 时，给每一段的 \(V_i\) 都变为 \(V_i-k\)。给 dp 数组设为 pair，first 存 \(h(x)\)，second 存 \(x\)。因为我们要保证的是 \(g(x)\) 最小，\(x\) 仅做辅助记录（因为最后还要加上 \(kx\)），如若这个函数没有单调性，\(x\) 也需要取最小值，因为其不存在反函数，一个 \(g(x)\) 可能对应两个 \(x\)。

wqs 二分中，如若 second（即 \(x\)）小于你二分的段数了，那么 \(k\) 需要增加。感性理解上就是你 \(k\) 越大，段数越多，稍微严谨一点就是，你的斜率越大，你切的越往上，\(x\) 越大，那你做完了。最后判一下 \(kx+b\leq n - k\) 即可。