Atcoder Regular Contest 162 题解

[ARC162A] Ekiden Race

正难则反。考虑一个点不能获奖的充分必要条件。

即存在 \(j>i\) 使得 \(p_j<p_i\)，这表明 \(j\) 去程时间长，且总程比 \(i\) 短，那么回程必然比 \(i\) 短。

暴力枚举 \(O(n^2)\) 可过，可以用树状数组优化到 \(O(n\log n)\)。

[ARC162B] Insertion Sort 2

注意到暴力对序列进行修改复杂度是 \(O(n^2)\)，这是可以接受的。且你的策略与普通排序基本相同，设已经排序好的最大数为 \(x\)，则暴力找到 \(x+1\) 的位置并向前交换修改。

分类讨论：

1. 如果 \(x+1\) 的位置不为 \(n\)，那么设其位置为 \(pos\)，将数对 \((a_{pos},a_{pos+1})\) 向前交换到指定位置。

2. 如果 \(x+1\) 的位置在 \(n\)，那么不能直接换，你需要尽量不影响前面已经排序的数的情况下，把数 \(x+1\) 的位置改到非 \(n\)，且要用最少的步数。于是把 \((a_{n-3},a_{n-2})\) 和 \((a_{n-1},a_n)\) 交换。这样就把第二种情况归约成了第一种情况。

无解分析：如果 \(2\) 操作必定会影响前面已经排好序的数，那么就无解。实现上，不用考虑直接在最后 check 一下即可。

操作次数分析：每个数归位最多只会被操作两次，故总操作次数 \(\leq 2\times n=2\times 10^3\)。

[ARC162C] Mex Game on Tree

首先考虑 Bob 的策略，他怎样才能让子树 \(mex\) 不为 \(k\)，他可以把 \(\leq k\) 的数都填一遍，但是其实他有一个显然更优的策略。

\(Key\space Observation\) Bob 只需要暴力填 \(k\) 就可以让 \(mex\) 不为 \(k\)，证明显然。

接下来考虑 Alice 的策略，固定的，他要让某一棵子树填了 \(0\) 到 \(k-1\)，且不能填 \(k\)，其余随意。

那么我们定性分析这个博弈，可以直观感受到，在随机情况下，Bob 赢得概率远大于 Alice，只有树上的颜色结构满足一些特殊条件时，Alice 才有可能赢。

接下来模拟博弈过程：

1. Alice 放完一个数。
2. 假设 Alice 填在了点 \(u\)，如果下面 \(u\) 的子树内有空位的话，Bob 将 \(k\) 填在任意一个空位上，使 \(u\) 子树变为无效子树。（注意无效子树的定义，\(u\) 子树变为了无效子树后，也有可能存在一个 \(u\) 的儿子 \(v\)，使得 \(v\) 的子树是有效子树）

\(Key\space Observation \space 2\) 如果子树 \(u\) 里面有大于等于两个空位，且 Alice 想让子树 \(u\) 满足条件，那么 Alice 无论做什么操作必定无效，即 Bob 可以在 Alice 填完后立刻把 \(u\) 子树变为无效。

所以，一个子树想要满足条件，其内部只能有一个或零个空位，如果是 \(0\) 个，判断是否 \(1\) 到 \(k-1\) 这些颜色都在内，且 \(k\) 不在。\(1\) 个同理，使用 set check 即可。时间复杂度 \(O(n^2\log n)\)，精细实现可以做到 \(O(n^2)\)。

[ARC162D] Smallest Vertices

首先，枚举树这件事你是无法做到的，考虑到对答案有贡献的是点，于是显然的考虑对单点拆贡献。

对于一个根 \(u\)，如果想让 \(u\) 是好点，那么要满足以下条件：

1. \(u\) 子树内的点全部 \(\geq u\)。
2. 其余随意。
3. 设 \(u\) 子树的大小为 \(k\)，则 \(\sum_{v\in subtree(u)} d_v=k-1\)。

注意到第三个限制条件对度进行了限制，且 \(u\) 点有贡献的树的个数，可以描述为：为每个点的度有限制的两个树拼起来。所以我们自然的想到给定度，对合法树进行计数的结论。

结论：给定 \(n\) 个点的 \(deg_i\)，求合法树的个数，根据 Prufer 序列，其答案为 \(\frac{(n-2)!}{\prod (deg_i-1)!}\)。又因为题目给的是出度，那么 \(d_1=deg_1\)，\(d_i=deg_i-1(i\neq 1)\)。于是答案转化为 \(\frac{d_1(n-2)!}{\prod d_i!}\)。但是这个结论我确实没看懂咋证的。

我们假设有贡献的点为 \(v\)，其子树集合为 \(S\)，那么根据我们上面说的，就是合法 \(v\) 子树乘以合法的除去 \(v\) 子树的树个数的乘积。我们想求出答案。

我们有一个很棘手的问题，即如果我们把 \(v\) 子树整个删掉，其必然在 \(v\) 子树外会有一个点的度减 \(1\)，因为这条边连向了 \(v\)。我们想阻止这种情况的发生。

所以我们不删 \(v\)，而把除了 \(v\) 的 \(v\) 的子树删掉，同时，把 \(v\) 的所有出度删掉。由于 \(v\) 没有了出度，它就可以被当做叶子处理了。记 \(e_u(i)\) 为以 \(u\) 为根的情况下，\(i\) 点的 \(deg_i\)。

那么最终写出来的式子就是：

\[\frac{(|S|-2)!}{\prod_{i\in S}(e_v(i)-1)!}\times \frac{(n-|S|-2+1(this \space is \space v))!}{\prod_{i\notin S}(e_1(i)-1)!} \]

下面可以直接写 \(i\notin S\) 是因为 \(deg_v=0\)，我们可以直接把 \(v\) 去了。

经过变换，即可得到以下我们熟悉的形式：（注意到我们使用了两次以……为根的叙述，故上面还有一个 \(d_v\)）

\[\frac{(|S|-2)!(n-|S|-1)!d_1d_v}{\prod d_i!} \]

注意到差不多只和 \(|S|\) 和 \(d_v\) 有关了。

考虑 dp，设 \(f_{i,j,k}\) 为以 \(i\) 为根，选了 \(j\) 个点，点度和为 \(k\) 的方案数。设 \(g_{i,j,k}\) 为根为 \(i\) 及以后的数，选了 \(j\) 个点，点度和为 \(k\) 的方案数。

\[f_{i,j,k}=g_{i+1, j-1, k-d_i} \]

\[g_{i,j,k}=g_{i+1, j, k}+f_{i,j,k} \]

但是其实可以不要 \(f\)，每次查 \(g_{i+1, j-1, k-d_i}\) 即可，因为实际上出度之和比点数少 \(1\)，所以你询问的就是 \(g_{i+1, j-1, k-d_i-1}\)

求答案时，需要枚举 \(v\)，因为需要知道 \(d_v\)，然后你需要枚举一个 \(|S|\)，然后就按照那个式子转移就好了。

然后一些细节，如果这个东西是根或者它是个叶子，那它必然是一个好点，那他的贡献就是 \(\frac{d_1(n-2)!}{\prod d_i!}\)。

需要预处理的只有阶乘和阶乘逆元，复杂度瓶颈在于 dp，时间复杂度 \(O(n^3)\)。

[ARC162E] Strange Constraints

先考虑一个事，就是你一个数 \(i\) 比如想填 \(k\) 次，那么需要保证两个条件：

1. 保证 \(A_i\geq k\)。
2. 填在 \(A_t\geq k\) 的位置 \(t\)。

这启发我们固定次数，按照次数 dp。

然后考虑怎么 dp，如果两个数 \(k\) 和 \(t\) 且有 \(k<t\)，那么 \(\geq k\) 这个限制比 \(\geq t\) 这个限制要松。如果你从松到严 dp，那么我们考虑这么一个事情，如果存在一个位置 \(r\)，使得 \(A_r>k\) 且 \(A_r>t\)，那么 dp 到 \(k\) 时有可能选了位置，dp 到 \(t\) 时，我们就不知道有没有选过这个位置，于是这是有后效性的。

于是我们按照次数倒序 dp。这样如果我们知道了后面选的位置的总数，那么前面可选位置的总数我们也固定了。

我们记 \(g_i\) 为 \(A_i\geq i\) 的个数，第一维定出来之后，我们很显然的设定第二维和第三维为 \(f_{i,j,k}\) 表示你填到个数为多少的数，填了几种本质不同的数，总共占了多少个位置。那么显然的，我在 \(i\) 的情况下，每类数都必须填 \(i\) 个，如果设选的本质不同的数为 \(t\)，那么就从 \(f_{i+1,j-t,k-t\times i}\) 转移。

然后乘系数，即从 \(g_i-(j-t)\) 里选 \(t\) 个，即 \(\binom{g_i-(j-t)}{t}\)，然后选位置，即从 \(g_i-(k-i\times t)\) 里面选 \(i\times t\) 个，再乘上 \(\binom{g_i-(k-i\times t)}{i\times t}\)。你现在是组合，由于序列是有标号的，所以需要定序，就再乘上 \((i\times t)!\)，由于是多重集排列数，所以去重 \(\frac{1}{\prod num_i}\)，这里 \(num_i\) 都是 \(i\)，因为你定了每个数选多少个，所以就是乘 \(\frac{1}{(i!)^t}\)。

直接转移即可，复杂度 \(O(n^3)\)，但是不会证。

Bonus：你有没有一个疑问，第一个限制去哪了？答案是我上面乘的是 \(\binom{g_i-(j-t)}{t}\)，是从限制大于等于 \(i\) 的位置选的数，而并非 \(n\) 个数都可以选。

[ARC162F] Montage

感觉第二篇题解 dp 思路太巧妙了。且困难的在于推性质。

性质 \(1\)：如果 \(1\) 右边有一个 \(0\)，那么 \(0\) 的下面必然都是 \(0\)，这是显然的。

性质 \(2\)：如果 \(1\) 左边有一个 \(0\)，那么 \(0\) 的上面必然都是 \(0\)，对称的显然。

性质 \(3\)：如果 \(1\) 下边有一个 \(0\)，那么 \(0\) 的右面必然都是 \(0\)。

性质 \(4\)：如果 \(1\) 上边有一个 \(0\)，那么 \(0\) 的左面必然都是 \(0\)。

合起来得到性质 \(5\)，即若两个 \(1\) 在同一行，若其同行在两个 \(1\) 中间还有一个 \(0\)，那么 \(0\) 所在列都是 \(0\)。

根据性质 \(5\)，我们可以去掉全为 \(0\) 的列，这不太影响答案。

合起来得到性质 \(6\)，即若两个 \(1\) 在同一列，若其同列在两个 \(1\) 中间还有一个 \(0\)，那么 \(0\) 所在行都是 \(0\)。

根据性质 \(6\)，我们可以去掉全为 \(0\) 的行，这也不太影响答案。

在最终图上，我们得到性质 \(7\)，\(8\)，\(9\)，\(10\)。

性质 \(7\)：如果 \(1\) 下边有一个 \(0\)，那么 \(0\) 的右下矩阵必然都是 \(0\)。

性质 \(8\)：如果 \(1\) 上边有一个 \(0\)，那么 \(0\) 的左上矩阵必然都是 \(0\)。

性质 \(9\)：如果 \(1\) 左边有一个 \(0\)，那么 \(0\) 的左上矩阵必然都是 \(0\)。

性质 \(10\)：如果 \(1\) 右边有一个 \(0\)，那么 \(0\) 的右下矩阵必然都是 \(0\)。

我们动用一些眼力来发现性质 \(11\)。

*性质 \(11\)：如果左上角有一个 \(1\)，右下角有一个 \(1\)，那么整个矩形都是 \(1\)，用反证法不难说明。

那么我们发现，最终的图一定长这样：

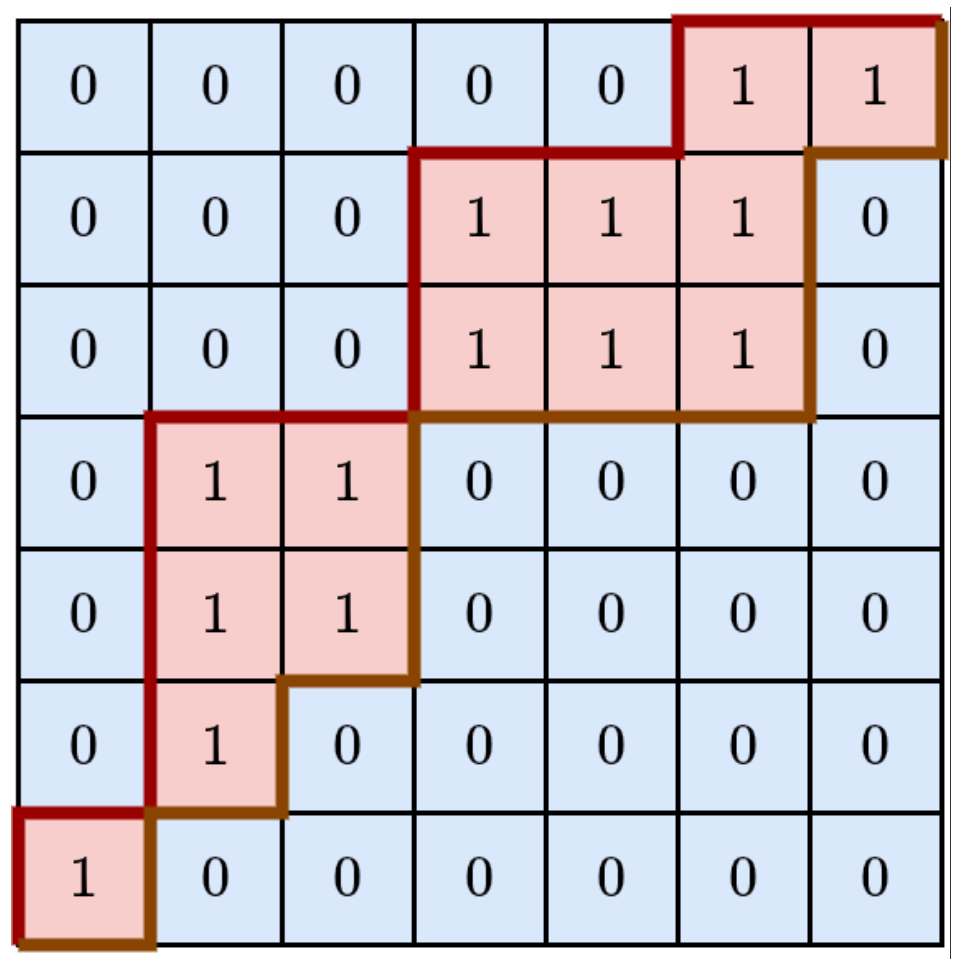
由一条红线和棕线围成的东西，且有一个性质，即两线触碰后会立即分开。

下面讲述这个神奇的 dp，但其实这个性质基本都见过。即在网格图上，从左下角开始走到右上角，只能向右或向上，你走第 \(k\) 步一定会走到 \(y=-x+k\) 的这条直线上，于是我们考虑根据 \(k\) 来 dp。

于是我们记 \(f_{i,j,k}\) 表示红色，棕色两条线被直线 \(y=-x+i\) 所截的两点分别为 \((j,i−j)\) 和 \((k,i−k)\) 对应的方案数。

这里的转移非常显然。

当 \(j=k\) 时，\(f_{i,j,k}\) 转移到 \(f_{i+1,j,k+1}\)。

当 \(j\neq k\) 时，任意转移即可。

最后再乘上 \(\binom{n}{i}\)，再乘上 \(\binom{m}{j}\) 即可，只要你想到这个不变量，就可以写出这个非常漂亮的 dp。