图论专栏

P1700

题面

有 \(n\) 个顶点，给出 \(n-1\) 条边，现在是要求是否存在一个点可以被所有点给指向，并且这个点的编号是最小的。

分析

思路1

反向建边，就变成了是否有一个点可以指向所有的点。

检测的这个部分可以用 dfs 或者 bfs 皆可。

思路2

由于 $n \le 100 $ ，所以直接暴力。

考虑每个点可以指向的所有边，然后看最小符合答案，即可暴力通过。

代码

思路2

#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> g;
vector<int> f;
bool vis[105];
int n;
void dfs(int u){
	if(vis[u]) return;
	vis[u]=1;
	for(int i=0;i<g[u].size();i++){
		f[g[u][i]]++;
		dfs(g[u][i]);
	}
}
int main(){
	scanf("%d",&n);
	f.resize(n+1,0);
	g.resize(n+1);
	for(int i=1,u,v;i<n;i++){
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
	}
	for(int i=1;i<=n;i++){
		memset(vis,0,sizeof(vis));
		dfs(i);
	}
	/*
	for(int i=1;i<=n;i++)
		printf("%d ",f[i]);
	printf("\n");
	*/
	for(int i=1;i<=n;i++){
		if(f[i]==n-1){
			printf("%d",i);
			return 0;
		}
	}
	printf("-1\n");
	return 0;
}

B3862

题面

有 \(n\) 个顶点和 \(m\) 条边构成的一个有向图。

输出 \(n\) 个数，第 \(i\) 个数表示编号为 \(i\) 的点能指向的最大编号的点的编号。

例如：

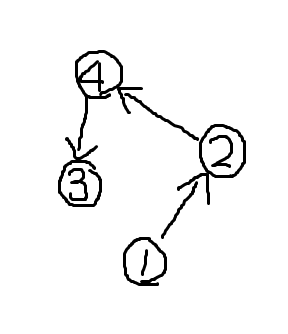
这种情况下，答案即为：

4 4 3 4

分析

一个点可以被某个点到达反过来说也可以到达可以到达这个点的点，那我们就可以反向建边。

处理完之后，在跑 n 次dfs找到访问过这个点的最大的点也就是答案存放在一个数组中。

最后输出这个数组。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
vector<int> g[N];
bool vis[N];
int a[N];
void dfs(int u,int i){
	if(vis[u])
		return;//如果已经被访问过就退出
	vis[u]=1,a[u]=i;//记录答案
	for(auto v: g[u])//找到所有可以访问当前这个点的点
		if(!vis[v]) dfs(v,i);
}
int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1,u,v;i<=m;i++)
		scanf("%d%d",&u,&v),g[v].push_back(u);//反向建边
	for(int i=n;i>=1;i--)
		dfs(i,i);//处理答案
	for(int i=1;i<=n;i++)
		printf("%d ",a[i]);
	return 0;
}

P1330

题面

有 \(n\) 个点，\(m\) 条边。

需要做的就是至少删除多少个节点才能使得这个图不连通。

特别地，删除的两个节点在被删除之前不能相连。

分析

可以知道一条线段如果一个端点被选中另一个就不能选择，所以在DFS的时候可以加一个染色转换，由于数据比较大，所以只能用邻接表存。

然后我们不断搜索就可以了。

代码

```plaintext
#include<bits/stdc++.h>
using namespace std;
vector<int> g[10010];
int n,m,c[10010],x,f[10010];
void dfs(int k,int t){
	if(c[k]!=-1&&c[k]!=t){
		printf("Impossible");
		exit(0);
	}
	if(c[k]==t) return;
	c[k]=t;
	f[k]=1;
	x++;
	for(int i=0;i<g[k].size();i++) dfs(g[k][i],t^1);
}
int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1,u,v;i<=m;i++){
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
		g[v].push_back(u);
	}
	int ans=0;
	memset(f,0,sizeof(f));
	for(int i=1;i<=n;i++)
		if(!f[i]){
			x=0;
			memset(c,-1,sizeof(c));
			dfs(i,0);
			int t=0;
			for(int i=1;i<=n;i++) t+=c[i]==1;
			ans+=min(t,x-t); 
		}
	printf("%d",ans);
	return 0;
}