4.2算术后的发展2
算术是数学中最古老的部分之一。在最初的算术、几何之后,数学发展出了更多的分支内容:代数、分析、拓扑、概率……本节的讲述涉及其中代数、分析的初等部分的内容。其中会讲到的一个问题是数学构建的虚拟性质。
算术之后,数学的发展首先是体现在“数”概念的扩展上。
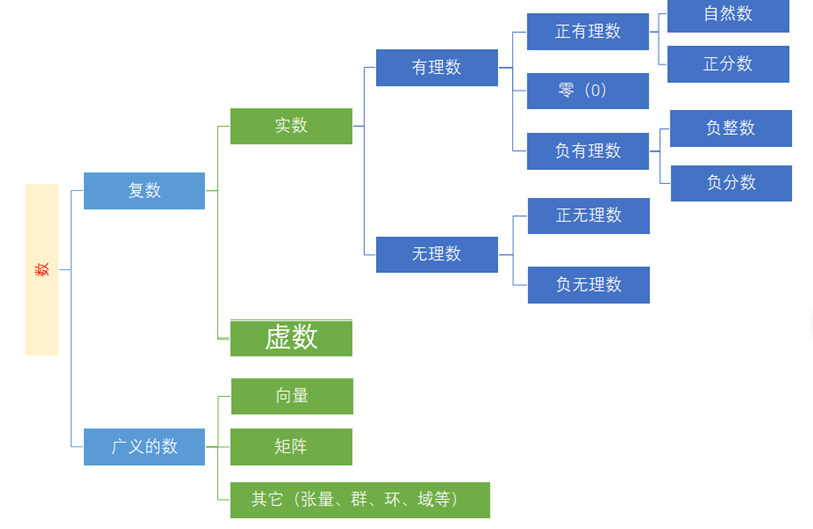
(图4-2:数系)
其次,数学的发展也体现在计算类型的扩展,从四则运算,到平方、开方、指数、对数的运算,微分、积分的运算……不同类型的数与不同类型的计算组成不同的计算系统,数学就是研究各种类型计算系统的性质与规律,并进一步抽象得到更一般的结构与关系。
就像在算术里一样,符号的恰当选择,表示上的进步,对数学各分支的发展也至关重要。字母符号的采用,使数学从算术进入到代数。早期的代数都是一个一个具体的问题,问题的求解也是各自独立的方法,问题描述与解题过程的说明都是文字的叙述,这时的代数也称为修辞代数。古希腊亚历山大港的数学家丢番图(Diophantus,246-330)开始自觉地使用从文字缩写或简写得到的符号来代表数,并使用字母来代表未知数,他开创的代数也称为缩写代数。现代意义上的符号代数,以字母来代表已知数、未知数,应用特定的运算符号以及等号的代数是文艺复兴时期产生的。早期重要的倡导者是法国数学家韦达(法语François Viète,1540-1603),他被称为现代符号代数之父。符号上的变化带来研究上的变化,以前一个一个的具体问题可以归为不同的方程,可以针对每类方程寻求统一的解题方法,运算规律可以以一般形式表达。历史上莱布尼茨与牛顿几乎同时发明了微积分,相较牛顿微积分,莱布尼茨对微积分符号的设计与选用有着更多考虑。他引入了微分符号dx、dy,将字母S(Summa)拉长得到“∫”作为积分符号。从效果来说,莱布尼茨的符号系统让微积分的概念与运算更加清晰,今天所用的微积分符号就是源自莱布尼茨的工作。按照莱布尼茨说法,能够选取恰当与简洁的符号,也将节省思维的劳动。
数学各分支早期阶段的发展,多是由实际问题推动。为测量土地发展出了最初的几何学;为进行贸易、分配财产发展出了算术;为了赢得赌博发展出了概率论……数学最初以实用的工具出现。数学进一步的发展则表现出虚拟构建的性质。比如数系的扩展,除了实践中会遇到不同类型数的问题外,更多是为了让算术运算、代数运算及其他的运算能够闭合,使计算规则具有普遍性而不断构造出的。为了减法运算始终可以施行构造了负数;为了除法运算始终可以施行构造了分数;为了开方运算始终可以施行构造了无理数、虚数,其中虚数是求负数的平方根时引入的……我们从一些实际问题里建立了一元一次方程:ax+b=0,对此类方程的求解进行了研究。之后不一定需要实际问题的输入,也不用天才的大脑,从一元一次方程的形式我们容易想到一元二次方程、一元三次方程、二元一次方程、二元二次方程等,然后我们可以去研究不同类型方程的解法。显然,一元一次方程简单清晰的表示,是后续扩展的良好基础。
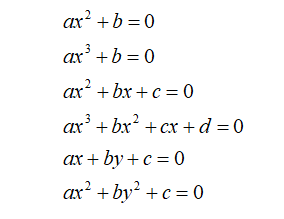
(图4-3:不同的方程)
数从自然数扩展到实数的过程中,对象的世界也发生了变化。算术与代数所面向的世界是离散事物数量的关系与变化,到了微积分(数学分析),所面向的世界是关于连续的量,如长度、面积、速度……离散与连续看似二个不同的世界,我们的做法是从算术、代数延伸发展出微积分,为此我们引入了“无限”的概念,用于填平二个世界间的鸿沟。这种做法目前来说是成功的,然而自引入无限概念以来,这一直是让人困惑与产生争论的地方,并且争论也将持续下去。
无限的问题在算术里就已出现。现实中我们能遇到的任一自然数只能是特定大小的数,位置记数法可表示任意大的自然数,这意味着它总能生成下一个更大的数,或者能生成无限多的自然数。在算术里,我们通过计数来建立实物数量与自然数符号的对应,对于连续量,我们通过测量将实际中一个连续的量与一个实数对应。测量的原理就是操作代表量度单位的实物来比较被测量的实物。每次测量值不一定是得到度量单位的倍数,否则就回到了算术的世界。存在小于当前度量单位的余量,此时需要换一个更小的度量单位来测余量,测量值就会对应一个小数。关键是任意度量单位下总可以假设会有余量,也就是除不尽的情况,对应无限循环小数,或无限不循环小数。
测量的操作对应着心智上对测量对象的分割拟想,分割动作可以无限地进行下去,实数就是在此分割中得到,每一步都得到一个实数,无限分割下去的结果就是得到致密的实数。但存在那些实数则是不能说清的。这不是真实会发生的情况,如果是测量某一实物的长度,实际的物质可找到更小的构成:分子、原子、质子与中子、电子、更基本的粒子……它们组成的实物并不一定呈均质可无限分割的情形。无限可分割只是心智上的拟想,基于此种拟想,虚拟出了符号里的连续世界,这种人造的尺度超出现实,最终也可应用于现实。只是结果的集合不可穷尽或不能明确揭示,甚至是不可构造的(超越数),这在理解上就很难说是清晰的。
实数是微积分的基础,在微积分的计算中,计算过程也是同样的性质,计算可以一直进行,不是操作到某一步就得到结果,也不是没有结果,结果作为一种极限存在,可以在无尽的操作中无限逼近这一结果,但不会构造地达到这一结果。分析上,我们采用大于、小于这些概念描述逼近极限的过程,这逻辑上没有问题,心理理解上则是另一回事。在后文中,我们将计数与测量合称为计量。
带有虚拟性构造的数学,最终可得到实际应用,这是一个不可思议的地方。同样的数学内容可为不同的领域规律或事实提供描述,并通过计算解释各种现象或解决各类实际问题。最先出现于牛顿物理学里的微积分,在经济学领域也被用来进行边际与弹性的分析,求解各种经济问题中最佳效益值。这符合前面对符号方式的描述,或者说可将数学视为一门语言。
数学的广泛应用,要求数学本身是可靠的。当数学已发展为枝繁叶茂的大树,其基础的可信与内部的无矛盾已不是那么显而易见。对此所进行的研究是推动数学发展的另一动力。由希尔伯特倡导,人们尝试将数学各分支进行公理化、形式化的整理,并采用集合论、一阶谓词逻辑等作为通用的描述形式,以此保障各数学分支的可靠性。其成果包括了前述的皮亚诺算术公理系统。不幸的是集合论中发现了悖论,引发了第三次数学危机,危机激发更多的研究,带来了现代数学中那些基础且抽象的分支。
随着数学的发展,更多类型的数与计算被扩展出来,如对数、指数的计算,三角函数的计算,微分、积分的计算……就算有纸笔媒介系统的辅助,这些计算对人而言也是困难、枯燥的。发明计算工具来快速、可靠地完成各类型的计算,是各个时代科研与生产上的需要。各种计算工具也应运而生,用来模拟纸面的符号计算:算盘、计算尺、帕斯卡加法器、莱布尼茨乘法器、巴贝奇的差分机……从木制的工具,到机械的工具,再到机电的工具。这些都是各时代心灵手巧的天才们的创造。



