ZYZ 数据结构研究所最新成果:路径折叠并查集。
这是最常见的带路径压缩和按秩合并的并查集模板:
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3f
using namespace std;
#ifdef ONLINE_JUDGE
#define getchar getchar_unlocked
#define putchar putchar_unlocked
#endif
int n,m;
int fa[200010],siz[200010];
static inline int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]);}
int main(){
read(n),read(m);
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;
while(m--){
int op,x,y;read(op),read(x),read(y);
x=find(x);
y=find(y);
if(op==1){
if(x==y) continue;
if(siz[y]>siz[x]) fa[y]=x,siz[x]+=siz[y];
else fa[x]=y,siz[y]+=siz[x];
}else{
if(x==y) putchar('Y');
else putchar('N');
putchar('\n');
}
}
return 0;
}
运行时间:747ms。
但是,这太慢了!(其实一点也不慢)
而在昨天,我发现了一种并查集的黑科技:
void pathzip(int&x){while(fa[x]!=x) x=fa[x]=fa[fa[x]];}
这种黑科技叫路径折叠。
顾名思义,就是直接把 x 到根的路径一次性全部折叠起来。
这是使用了路径折叠黑科技和按秩合并的并查集:
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3f
using namespace std;
#ifdef ONLINE_JUDGE
#define getchar getchar_unlocked
#define putchar putchar_unlocked
#endif
int n,m;
int fa[200010],siz[200010];
static inline void pathzip(int&x){while(fa[x]!=x) x=fa[x]=fa[fa[x]];}
int main(){
read(n),read(m);
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;
while(m--){
int op,x,y;read(op),read(x),read(y);
pathzip(x);
pathzip(y);
if(op==1){
if(x==y) continue;
if(siz[y]>siz[x]) fa[y]=x,siz[x]+=siz[y];
else fa[x]=y,siz[y]+=siz[x];
}else{
if(x==y) putchar('Y');
else putchar('N');
putchar('\n');
}
}
return 0;
}
运行时间:713ms。
可能有的人会说了,
那你这优化也不明显啊?这个黑科技有什么用呢?
这个黑科技最大的特性就在于:这玩意可以扩展!
比如上面用到的 x=fa[x]=fa[fa[x]]。
我们可以把它改成 x=fa[x]=fa[fa[x]]=fa[fa[fa[x]]]。
或者再继续嵌套改成 x=fa[x]=fa[fa[x]]=fa[fa[fa[x]]]=fa[fa[fa[fa[x]]]]。
你甚至还可以继续嵌套!
我个人将路径折叠中 fa 的最多嵌套层数称为这个路径折叠的层数。
而且经过我的测试,并查集板子题,使用层数为 \(4\) 的路径折叠,能跑得最快(652ms)。
或者说今年 S 组 T2 的 Kruskal 做法,如果使用 \(2\) 层的路径折叠,你就可以把你的 5.62s 变成 5.45s!
很神奇,不是吗?
省流:
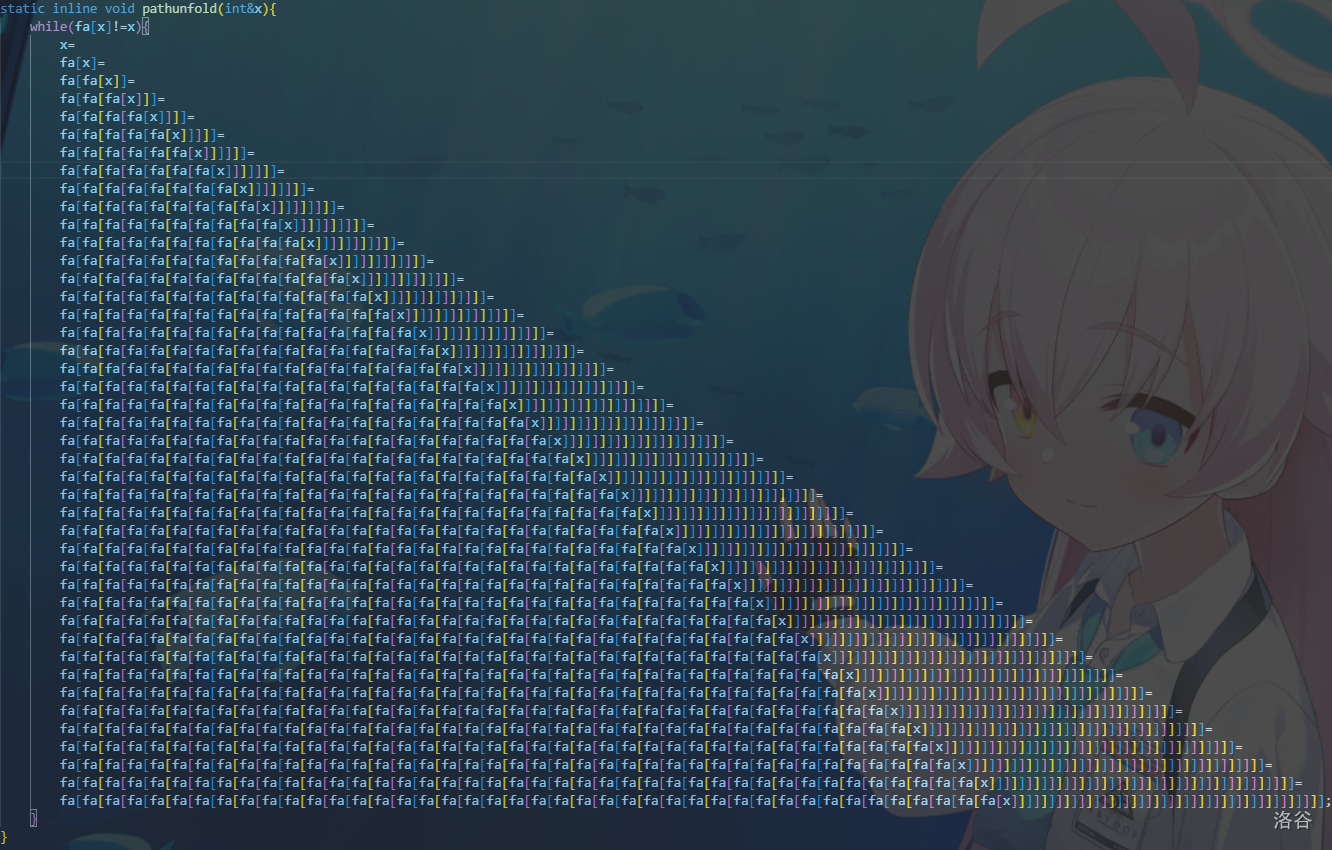



 浙公网安备 33010602011771号
浙公网安备 33010602011771号