关于caffe 是如何卷积的一点总结

　　最近，在看caffe源码时，偶然在网上看到一个问题？觉得挺有意思，于是，仔细的查了相关资料，并将总结写在这里，供大家迷惑时，起到一点启示作用吧。

       问题的题目是CNN中的一个卷积层输入64个通道的特征子图，输出256个通道的特征子图，那么，该层一共包含多少个卷积核？

对于上面这个问题，目前有两种答案，每一种答案的区别是所基于的卷积核的维度不同而导致的。下面是两种答案的解析过程：

第一种答案：卷积核是二维的（caffe源码中以卷积核二维转化成相应矩阵），那么就需要64*256个卷积核来对输入特征子图进行卷积，其中，输入的每个通道对应64种不同的卷积核进行卷积，再将64种卷积核得到的卷积结果合并成一张输出特征子图；这样，就会得到256个通道的特征子图。

第二种答案：卷积核是三维的(caffe大神贾杨清老师的回答中就是这么认为的)，那么一个卷积核的表示为C*H*W（C：通道数，H：卷积核的高，W：卷积核宽）。那么对于输入的特征子图，就需要一个大小为64*h*w的卷积核进行卷积，得到一张特征子图。这样，就需要256个不同卷积核，每个卷积核的通道数为64，从而得到256个通道的特征子图。

　　显然，这两种答案都有一定的依据，不管如何认为，其最终的目的都是要将卷积层复杂的卷积问题转化为矩阵的相乘问题，从而大大的提高计算速度。

　　那么，肯定有很多朋友，尤其是像我这种深度学习的菜鸟，一开始还是比较迷糊的，对于上面的解释还是不知所云。那么，下面，我就来对这两种观点进行具体分析，不足之处，希望大家能指出来，共同学习。

一，卷积核是二维的：

　　我们知道，在caffe中卷积层的运算是首先通过img2col()将各个卷积核和输入特征子图转化为向量，然后多个卷积核或输入特征子图的向量组合成为矩阵；接下来，通过矩阵相乘运算得到卷积的结果，再通过col2img()将向量转化为特征子图。M个卷积核卷积一张输入图像的矩阵计算如下图所示:

图来自http://www.cnblogs.com/laiqun/p/6055498.html

其中，M表示二维卷积核的个数，K=k*k表示二维卷积核的大小；这样，每个k*k大小的二维卷积核转化为一个行向量，M个二维卷积核对应M个行向量就得到了M*K的卷积矩阵A。

再说矩阵B:假设输入的每张特征子图大小为r*r，二维卷积核的大小为k*k，扩展大小pad，步长为stride，那么对于每张特征子图，按卷积核每次卷积图像的大小k*k，将该块卷积的图像转化为行向量，长度也为k*k=K，这样，依据卷积核与输入图像卷积的过程，将每一次卷积核卷积的区域转化为一个行向量，各个行向量按照卷积先后顺序以列进行排列，从而得到了矩阵B。此外，对于卷积后得到的二维特征子图的大小，在caffe中的计算公式如下(这里假设，输入图像和卷积和大小都是q*q的，即长与宽相等)：

　　输出特征子图大小:n*n=[(r+2*pad-k)/strde+1]*[(r+2*pad-k)/strde+1]

如果我们令pad=0，stride=1，那么就会变成我们熟悉的形式，即n*n=[(r-k)+1]*[(r-k)/+1]。比如，输入特征图大小为32*32，卷积核大小为3*3，那么输出的特征子图大小为(32-3+1)*(32-3+1)=28*28。

　　好了，现在我们知道了矩阵B的列N=n*n，然后通过矩阵相乘运行，即A*B^T=(M*K)*(N*K)^T=(M*K)*(K*N)=(M*N)=C，即得到了最终的矩阵C。当然，在caffe中可能会存在偏置项，那么这个矩阵C还要加上偏置矩阵P，然后得到最终的输出矩阵D，再通过col2img()将D中的每一行转化为一张特征图，就得到了输出的各个特征子图,从而完成了该卷积层的卷积运算。

二，卷积核是三维的：

　　对于卷积核是三维的情况，主要参考的是贾杨清老师在知乎上的一个解答。即认为每个输入图像和每个卷积核的大小表示为C*H*W，即：

 

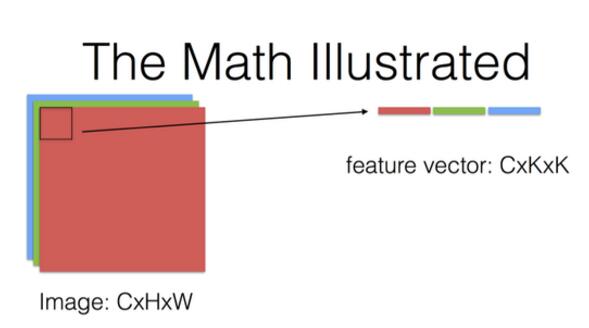
　　由上图知道，一个输入特征图的表示是C*H*W（通道数*长*宽），一个卷积核的大小表示为C*K*K(注意：这里，如果认为卷积核是三维的，就必须保证卷积核的通道数跟输入特征图的通道数相同，否则卷积失败)，那么根据卷积核一次卷积的图像区域，将该区域图像转化为行向量，即得到一个C*k*k的行向量。

　　按此方式，将一张图像按照卷积的顺序得到的行向量按列排列，就得到了最终的特征矩阵如下：

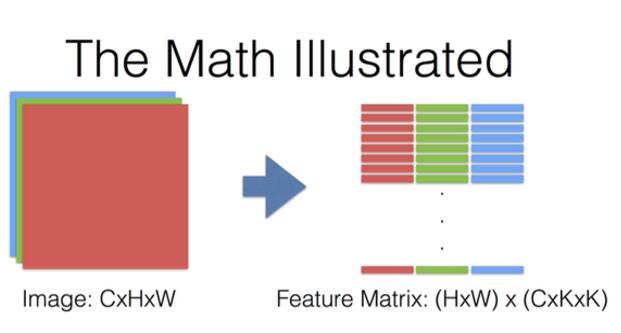上图知道，对于一个C*H*W的图像，按照卷积核大小进行卷积，转化为的特征矩阵大小为：(H*W)*(C*K*K)。

那么，对于多个卷积核而言，将多个卷积核转化为卷积矩阵过程如下：

这里，卷积核的个数为C_out，每个卷积核的大小为C*K*K，同理，将每个卷积核转化为一个行向量C*K*K，按照卷积核个数按列排列，就得到卷积矩阵C_out*(C*K*K)。

　　最后，将卷积矩阵与输入特征矩阵的转置进行相乘，就得到了最终的输出特征矩阵[C_out*(C*K*K)]*[(H*W)*(C*K*K)]^T=[C_out*(C*K*K)]*[(C*K*K)*(H*W)]=C_out*(H*W)。这样，再将输出矩阵的每一行转化为一张特征图，就得到了C_out张输出特征子图。而这，也就印证了：卷积层输出的特征图个数等于卷积核的个数。

　　以上，就是对两种对于卷积核的维度不同看法的具体分析，不管怎么定义，都有其充分的理由和实践证明。并且，最重要的是，不管卷积核定义为二维还是三维，都是为了数据转化为矩阵的形式，从而将卷积层的复杂的卷积过程，转化为矩阵的相乘的简单运算，大大的提高了计算的速度。

　　最后，通过一个具体的例子，来看一下将卷积转化为矩阵运算的过程：

 

参考链接：http://www.cnblogs.com/laiqun/p/6055498.html

　　　　　https://www.zhihu.com/question/28385679

　　　　　Convolution in Caffe: a memo · Yangqing/caffe Wiki · GitHub　

              High Performance Convolutional Neural Networks for Document Processing
              https://hal.archives-ouvertes.fr/file/index/docid/112631/filename/p1038112283956.pdf