洛谷P1471 方差
洛谷P1471 方差
题目背景
滚粗了的HansBug在收拾旧数学书,然而他发现了什么奇妙的东西。
题目描述
蒟蒻HansBug在一本数学书里面发现了一个神奇的数列,包含N个实数。他想算算这个数列的平均数和方差。
输入输出格式
输入格式:
第一行包含两个正整数N、M,分别表示数列中实数的个数和操作的个数。
第二行包含N个实数,其中第i个实数表示数列的第i项。
接下来M行,每行为一条操作,格式为以下两种之一:
操作1:1 x y k ,表示将第x到第y项每项加上k,k为一实数。
操作2:2 x y ,表示求出第x到第y项这一子数列的平均数。
操作3:3 x y ,表示求出第x到第y项这一子数列的方差。
输出格式:
输出包含若干行,每行为一个实数,即依次为每一次操作2或操作3所得的结果(所有结果四舍五入保留4位小数)。
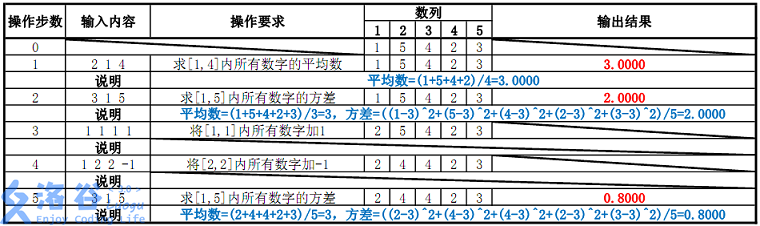
输入输出样例
说明

样例说明:
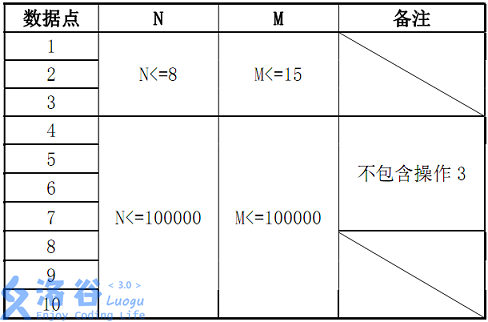
数据规模:
题解:看到这种N,M≤100000的数据范围,想必是要用O(Mlog2N)的方法来做的了。
很显然,这个题目有区间修改和区间询问,因此我们用线段树来维护。
我们会发现,这题与直接维护加法和乘法的线段树有相似之处,所以本题的关键是如何维护平均数和方差。
于是这题就不如直接维护加法和乘法的线段树来的直接了,我们还要进行一些式子的推理。如果你还不熟悉线段树本身的算法,请参考模板题洛谷P3372和P3373。
根据方差的定义,我们可以展开得到如下式子:
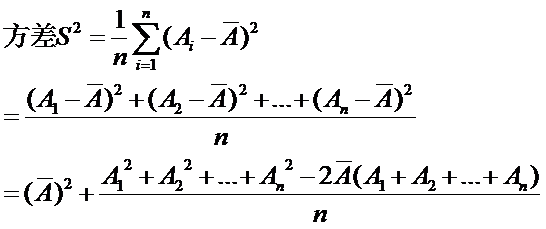
从这里就可以看出我们维护区间[L,R]的区间和,就可以同时维护出平均数(因为平均数等于区间和除以区间长度)。那么我们只需要再维护区间的平方和就可以了。
该题自然还是要用懒标记的,懒标记只需要记录一个,因为修改操作只有一种。那么在下放懒标记时,怎样修改区间和与区间平方和呢?
区间和的修改自然是很简单的,与洛谷P3372和P3373的加法维护是一样的,主要是维护区间平方和。
我们可以知道,如果给一个区间的每一个数加上一个数k,平方和就会发生变化,将此变化列式展开得:

于是,新的平方和就可以通过原区间的区间和,区间长度与懒标记共同维护。
要注意,先修改区间平方和,再修改区间和。因为根据上式,区间平方和是需要借助原区间的区间和更新的。
这就是本题的要点,细节详见代码。

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const int N=100005; 5 struct node{ 6 int l,r,len; double sum,sqrsum,lazy; 7 }tree[N<<2]; 8 int n,m,opt,x,y; 9 double k; 10 double sqr(double x){ 11 return x*x; 12 } 13 node operator + (node a,node b) 14 { 15 node c; c.lazy=0; 16 c.l=a.l; c.r=b.r; 17 c.len=a.len+b.len; 18 c.sum=a.sum+b.sum; 19 c.sqrsum=a.sqrsum+b.sqrsum; 20 return c; 21 } 22 void build(int u,int l,int r) 23 { 24 tree[u].l=l; tree[u].r=r; 25 if (l==r) 26 { 27 scanf("%lf",&tree[u].sum); 28 tree[u].sqrsum=sqr(tree[u].sum); 29 tree[u].len=1; tree[u].lazy=0; 30 return; 31 } 32 int mid=(l+r)>>1; 33 build(u<<1,l,mid); 34 build(u<<1|1,mid+1,r); 35 tree[u]=tree[u<<1]+tree[u<<1|1]; 36 } 37 void push_down(int u) 38 { 39 if (tree[u].lazy) 40 { 41 tree[u<<1].sqrsum+=tree[u<<1].len*sqr(tree[u].lazy)+2*tree[u].lazy*tree[u<<1].sum; 42 tree[u<<1|1].sqrsum+=tree[u<<1|1].len*sqr(tree[u].lazy)+2*tree[u].lazy*tree[u<<1|1].sum; 43 tree[u<<1].sum+=tree[u<<1].len*tree[u].lazy; 44 tree[u<<1|1].sum+=tree[u<<1|1].len*tree[u].lazy; 45 tree[u<<1].lazy+=tree[u].lazy; 46 tree[u<<1|1].lazy+=tree[u].lazy; 47 tree[u].lazy=0; 48 } 49 } 50 void change(int u,int l,int r,double v) 51 { 52 if (tree[u].l==l&&tree[u].r==r) 53 { 54 tree[u].lazy+=v; 55 tree[u].sqrsum+=tree[u].len*sqr(v)+2*v*tree[u].sum; 56 tree[u].sum+=tree[u].len*v; 57 return; 58 } 59 int mid=(tree[u].l+tree[u].r)>>1; 60 push_down(u); 61 if (r<=mid) change(u<<1,l,r,v); 62 else if (l>mid) change(u<<1|1,l,r,v); 63 else change(u<<1,l,mid,v),change(u<<1|1,mid+1,r,v); 64 tree[u].sum=tree[u<<1].sum+tree[u<<1|1].sum; 65 tree[u].sqrsum=tree[u<<1].sqrsum+tree[u<<1|1].sqrsum; 66 } 67 node query(int u,int l,int r) 68 { 69 if (tree[u].l==l&&tree[u].r==r) return tree[u]; 70 int mid=(tree[u].l+tree[u].r)>>1; 71 push_down(u); 72 if (r<=mid) return query(u<<1,l,r); 73 if (l>mid) return query(u<<1|1,l,r); 74 return query(u<<1,l,mid)+query(u<<1|1,mid+1,r); 75 } 76 int main() 77 { 78 scanf("%d%d",&n,&m); 79 build(1,1,n); 80 for (int i=1;i<=m;++i) 81 { 82 scanf("%d",&opt); 83 if (opt==1) scanf("%d%d%lf",&x,&y,&k),change(1,x,y,k); 84 if (opt==2) 85 { 86 scanf("%d%d",&x,&y); 87 node tmp=query(1,x,y); 88 printf("%0.4lf\n",tmp.sum/tmp.len); 89 } 90 if (opt==3) 91 { 92 scanf("%d%d",&x,&y); 93 node tmp=query(1,x,y); 94 double ave=tmp.sum/tmp.len; 95 printf("%0.4lf\n",sqr(ave)+(tmp.sqrsum-2*ave*tmp.sum)/tmp.len); 96 } 97 } 98 return 0; 99 }



