全局最小割 stoer-wagner与karger-stein算法
stoer-wagner算法
进行n轮操作，每轮操作确定一对点s,t被割开情况下的最小割，然后将s,t合并。s,t为操作中最后剩下的两个点。
操作类似prim求最大生成树，每次将与当前集合相邻的距离最大的点合并到集合中，最后剩下s,t两点。
代码来自wiki
const int maxn = 550; const int inf = 1000000000; int n, r; int edge[maxn][maxn], dist[maxn]; bool vis[maxn], bin[maxn]; void init() { memset(edge, 0, sizeof(edge)); memset(bin, false, sizeof(bin)); } int contract( int &s, int &t ) { // Find s,t memset(dist, 0, sizeof(dist)); memset(vis, false, sizeof(vis)); int i, j, k, mincut, maxc; for(i = 1; i <= n; i++) { k = -1; maxc = -1; for(j = 1; j <= n; j++)if(!bin[j] && !vis[j] && dist[j] > maxc) { k = j; maxc = dist[j]; } if(k == -1)return mincut; s = t; t = k; mincut = maxc; vis[k] = true; for(j = 1; j <= n; j++)if(!bin[j] && !vis[j]) dist[j] += edge[k][j]; } return mincut; } int Stoer_Wagner() { int mincut, i, j, s, t, ans; for(mincut = inf, i = 1; i < n; i++) { ans = contract( s, t ); bin[t] = true; if(mincut > ans)mincut = ans; if(mincut == 0)return 0; for(j = 1; j <= n; j++)if(!bin[j]) edge[s][j] = (edge[j][s] += edge[j][t]); } return mincut; }
--------------------------------------------------------------------------------------------------------
对于特殊的所有边权值都为1的全局最小割，存在复杂度更低但常数较大的karger-stein算法
考虑store-wagner的缩边的过程。如果随机取边，正确性会怎样呢？
假设最小割为k，则边数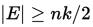 
。选中最小割中任意一条边的概率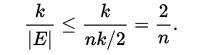
将这条边缩去重复直到只剩两个点，每一步都不选中最小割中边的概率为
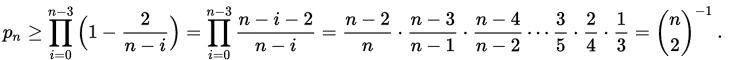
这样我们重复n2logn次失败的概率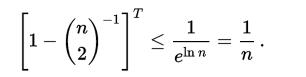
，此处使用了e的定义式
于是我们得到了在n^2mlogn时间复杂度下，1/n正确率的算法
在进行这个过程时每当图的点数变为原图的1/√2时，记录当前状态后进行两次对该状态的求解
这个做法的正确概率为
，
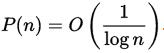
时间复杂度为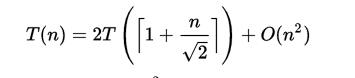
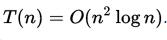
重复log2n次，我们就可以得到在n^2log^3n的复杂度下达到1./n正确性的算法
在实际测试中的表现
10次Karger-stein stoer-wagner
n=2000 40s 10s
n=5000 340s 134s
但是在这种情况下Karger-stein的正确率都大于1/2，有一定的优越性。
另外，所有最小割在Karger-stein运行过程中未被找到的数量的期望是1/n，几乎可以找到所有合法的最小割。
#include <cstdio> #include <algorithm> #include <cmath> #include <map> #define ULL unsigned long long #define LDB long double using namespace std; ULL sed=233; int top,deg[5010],b[5010][5010],totdeg,n,m,succ[5010],prev[5010],faqcnt=0; map <int,int> mp; struct data{ int x,y,k,num; }sta[5000*5000+1]; ULL ran(){ sed*=1280313;sed+=12413;sed^=123893; return(sed); } void restore(int tar){ while (top>tar){ data t=sta[top];top--; int x=t.x,y=t.y,i=t.k,num=t.num; if (t.k==-1){ deg[x]+=num;deg[y]+=num; b[x][y]=b[y][x]=num; totdeg+=2*num; succ[prev[x]]=x;prev[succ[x]]=x; }else{ deg[x]+=num;deg[y]-=num; b[y][i]=(b[i][y]-=num); b[x][i]=b[i][x]=num; } } } void contract(int x,int y){ sta[++top]=(data){x,y,-1,b[x][y]}; deg[x]-=b[x][y];deg[y]-=b[x][y]; totdeg-=2*b[x][y]; b[x][y]=b[y][x]=0; prev[succ[x]]=prev[x];succ[prev[x]]=succ[x]; for (int i=0;i<=n;i=succ[i]) if (b[x][i]){ sta[++top]=(data){x,y,i,b[x][i]}; deg[x]-=b[x][i];deg[y]+=b[x][i]; b[y][i]=(b[i][y]+=b[x][i]); b[x][i]=b[i][x]=0; } } void del(){ int tar=ran()%totdeg+1,x,y; for (x=0;tar>deg[x];tar-=deg[x],x=succ[x]); for (y=0;tar>b[x][y];tar-=b[x][y],y=succ[y]); contract(x,y); } int slowsolve(int po){ int ttop=top; for (int i=1;i<=po-2;i++) del(); int ret=totdeg/2; restore(ttop); return(ret); } int fastsolve(int po){ int ttop=top,ret=1e9;mp[po]++; if (po<=20){ int ret=1e9; for (int i=1;i<=100;i++){ ret=min(ret,slowsolve(po)); restore(ttop); } return(ret); } int tar=ceil(1+po/sqrt(2)); for (int i=1;i<=po-tar;i++) del(); ret=min(ret,fastsolve(tar)); restore(ttop); for (int i=1;i<=po-tar;i++) del(); ret=min(ret,fastsolve(tar)); restore(ttop); return(ret); } int main(){ scanf("%d%d",&n,&m); prev[n+1]=n;succ[0]=1; for (int i=1;i<=n;i++) prev[i]=i-1,succ[i]=i+1; for (int i=1;i<=m;i++){ int t1,t2; scanf("%d%d",&t1,&t2); deg[t1]++;deg[t2]++;b[t1][t2]++;b[t2][t1]++; totdeg+=2; } int ans=1e9; for (int i=1;i<=10;i++){ int t=fastsolve(n); ans=min(ans,t); printf("%d\n",t); } printf("%d\n",ans); }
