10.动态规划（3）——0-1背包问题

　　在上一篇《9.动态规划（2）——子集和问题》中，谈到了什么是子集和问题，以及实现。背包问题实际也是子集和问题的一种，不过背包问题不是“判断问题”而是一个“最优问题”。而背包问题实际上又分为“0-1背包”，“完全背包”，本文对“0-1背包”进行讲解。

　　问题：有n个物品，每个物品的重量为weigh[i]，每个物品所对应的价值为price[i]，现在有一个背包，背包所能承受的重量为W，问背包能装下的物品总价值最大是多少？

　　定义s[i, j]表示前i个物品的总价值，j为背包的承重量。当j = W或者最接近于W且小于W时，此时就是问题的解。

　　对于“动态规划”的关键就是要找到其递推公式，递推公式往往会将一个问题以某个值为边界拆分为两部分。背包问题的求解是子集和问题的最优化求解，在《9.动态规划（2）——子集和问题》中分析过递推公式的推导工程，在这里重新分析推导。

　　分析：s[i, j]表示前i个物品，如果前i - 1个物品价值已经达到背包承重量j的极限，那么第i个物品就不能放进去(j - wi < 0)，此时就可表示s[i, j] = s[i - 1, j]。但如果第i - 1个物品未达到背包承重量j的极限(j - wi >= 0)，此时我们计算前i - 1个物品的价值就是s[i - 1, j - wi]，此时加上第i个物品的价值就可以表示为s[i - 1, j - wi] + pi。

　　综上得到递推公式：

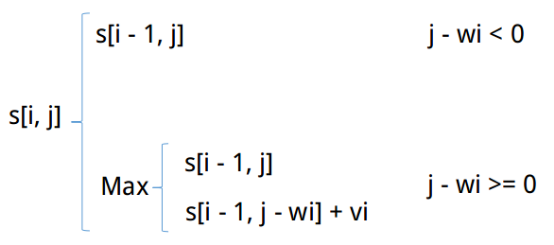
　　举例：物品的重量集合w = (2, 4, 1, 5, 3)，物品的价格集合 p = (4, 5, 19, 3, 2)，背包重量6。通过上面的递推公式，将这个背包问题利用矩阵来表示，第6列的最大值即为背包重量为6时的最大价值。

　　Java

package com.algorithm.dynamicprogramming;

import java.util.Arrays;

/**
 * 0-1背包问题
 *           | s[i - 1, j]                      (j - wi < 0)
 * s[i, j] = |     | s[i - 1, j]
 *           | Max |                            (j - wi >= 0)
 *           |     | s[i - 1, j -wi] + pi
 * Created by yulinfeng on 7/3/17.
 */
public class KnapsackProblem {
    public static void main(String[] args) {
        int[] weight = {2, 4, 1, 5, 2};
        int[] price = {4, 5, 19, 3, 2};
        int knapsackWeight = 6;
        int value = knapsackProblem(weight, price, knapsackWeight);
        System.out.println(value);
    }

    /**
     * 动态规划求解0-1背包问题
     * @param weight 物品重量
     * @param price 物品价值
     * @param knapsackWeight 背包承重量
     * @return
     */
    private static int knapsackProblem(int[] weight, int[] price, int knapsackWeight) {
        int row = weight.length + 1;
        int col = knapsackWeight + 1;
        int[][] solutionMatrix = new int[row][col];
        int[] values = new int[row];
        values[0] = 0;
        for (int i = 0; i < row; i++) {
            solutionMatrix[i][0] = 0;
        }
        for (int j = 0; j < col; j++) {
            solutionMatrix[0][j] = 0;
        }

        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                solutionMatrix[i][j] = solutionMatrix[i - 1][j];
                if (j - weight[i - 1] >= 0 && solutionMatrix[i - 1][j - weight[i - 1]] + price[i - 1] > solutionMatrix[i][j]) {
                    solutionMatrix[i][j] = solutionMatrix[i - 1][j - weight[i - 1]] + price[i - 1];
                }
            }
            values[i] = solutionMatrix[i][col - 1];
        }
        Arrays.sort(values);
        return values[values.length - 1];
    }
}

　　Python3

def knapsack_problem(weight, price, knapsackWeight):
    '''
    0-1背包问题
              | s[i - 1, j]                      (j - wi < 0)
    s[i, j] = |     | s[i - 1, j]
              | Max |                            (j - wi >= 0)
              |     | s[i - 1, j -wi] + pi

    Created by yulinfeng on 7/3/17.
    '''
    row = len(weight) + 1
    col = len(price) + 1
    solutionMatrix = [[0 for c in range(col)] for r in range(row)]
    values = [0] * row
    for i in range(row):
        solutionMatrix[0][i] = 0
    for j in range(col):
        solutionMatrix[j][0] = 0
    for m in range(1, row):
        for n in range(1, col):
            solutionMatrix[m][n] = solutionMatrix[m - 1][n]
            if n - weight[m - 1] >= 0 and solutionMatrix[m - 1][n - weight[m - 1]] + price[m - 1] > solutionMatrix[m][n]:
                solutionMatrix[m][n] = solutionMatrix[m - 1][n - weight[m - 1]] + price[m - 1]
        values[m] = solutionMatrix[m][col - 1]
    
    values.sort()
    return values[len(values) - 1]

weight = (2, 4, 1, 5, 2)
price = (4, 5, 19, 3, 2)
knapsackWeight = 6
value = knapsack_problem(weight, price, knapsackWeight)
print(value)