识别猫的单隐藏层神经网络（我的第一个模型）

摘要：算法详解；代码；可视化查看超参数影响

目标：识别一张图是不是猫

数据集：训练数据209张64*64

        测试数据50张 64*64

方案：二分分类法

算法：logistic回归 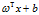，限定了你的输入（X），和做优化时，需要优化哪些量(W,b)

激活函数：sigmod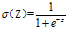

sigmod函数图像：

特点：所有输出y值都落在0-1之间

ps：logistic回归是算法，但其激活函数取sigmod，是因为，你想得到一个在（0-1）之间的值，所以，这才用到了sigmod函数。

 

损失函数：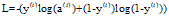

成本函数：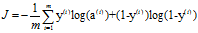

成本函数的由来：假设第1张图真实值是1（第一张图本来就是猫），

预测时，认为

它是猫的概率是0.8，体现在sigmod函数输出0.8,（a=0.8）

则正确率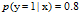

同理，如果假设某图不是只猫，其y=0，

其正确率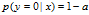

合并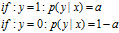

得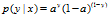

log是一个单调递增的函数，可以变成一个凸函数，便于使用梯度下降进行优化

把上式log化

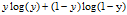
上式还不是成本函数，因为，上式值越大表明，越准确

按照习惯来说，需要成本函数越小，预测值与真实值越接近，越准确

所以，直接加个负号就行了

所以，成本函数就是

 

计算图

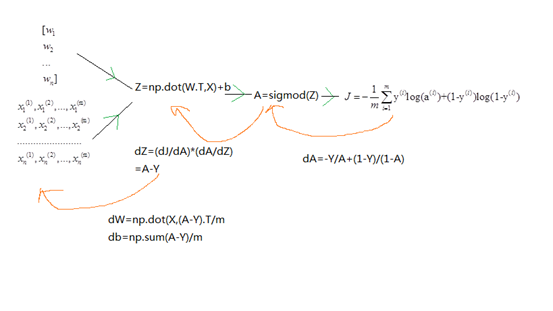
代码：

1. 载入数据
2. 处理数据（/255），缩小数据，因为1比255更好计算
3. 初始化（w，b），w是一个n维列向量，b=0
4. 建立sigmod函数
5. 利用训练数据集 建立正反向传播函数，如计算图，并求梯度，以便使用梯度下降
6. 建立优化（梯度下降）函数，利用好梯度，选取下降方向，另需选取学习率，迭代次数。这两个选取与过拟合，欠拟合息息相关
7. 利用迭代num_iterations次后，出来的w，b。组装好sigmod函数，预测，测试集数据
8. 测试/训练集 正确率输出，利于判断
9. 可视化输出，比较出一个好的学习率，和迭代次数。（超参数选择，一个无法学习的东西

 

1. import numpy as np  
2. import matplotlib.pyplot as plt  
3. import h5py  
4. import sys  
5. sys.path.append(r'F:\study\assignment2')  
6. from lr_utils import load_dataset  
7. ''''' 
8. 数据读取与标准化 
9. 读取的x数据是（209，64,64,3）的格式 
10. 需要将其平铺成（64*64*3,209） 
11. '''  
12. train_x_orig,train_y_orig,test_x_orig,test_y_orig,classes=load_dataset()  
13.     
14. train_x_flatten=train_x_orig.reshape(train_x_orig.shape[0],-1).T  
15. test_x_flatten=test_x_orig.reshape(test_x_orig.shape[0],-1).T  
16. #上面一定要记得转置，因为reshape成了（m，n）的形式  
17. #-1，是不用去考虑到底要转换成多少列了，只要是负数就行  
18.     
19. #然后是将数据缩小，便于计算，因为1比255更好计算，反正也不影响计算机结果  
20. #标准化数据 rgb值都小于255的  
21. train_x=train_x_flatten / 255  
22. test_x=test_x_flatten / 255  
23.     
24. train_y=train_y_orig  
25. test_y=test_y_orig  
26. #上面就把数据整理好了  
27.     
28. ''''' 
29. 下面开始写函数了 
30. '''  
31.     
32. #建立sigmod函数  
33. def sigmod(x):  
34.     return (1/(1+np.exp(-x)))  
35.     
36. #初始化w，b, ps：w是一个列向量  
37.     
38. def initialize(n_x):  
39.     w=np.zeros(shape=(n_x,1))  
40.     b=0  
41.     return(w,b)  
42.     
43.     
44. #建立正反向传播函数  
45.     
46. def propagate(w,b,X,Y):  
47.     """ 
48. 正向传播 
49. """  
50.     
51.     A=sigmod(np.dot(w.T,X)+b)  
52.     m=X.shape[1]  
53.     cost=(-1/m)*np.sum(Y * np.log(A)+(1-Y) * np.log(1-A))  
54.     '''''  ps:尼玛不知道为什这个三点冒号也要按照缩进格式来 
55. 反向传播 
56. '''  
57.     dw=np.dot(X,(A-Y).T)/m  
58.     db=np.sum(A-Y)/m  
59.     
60.     ''''' 
61. 组装数据 
62. '''  
63.     grads={'dw':dw,'db':db}  
64.     return (grads,cost)  
65.     
66. #建立优化函数  
67.     
68. def optimize(w,b,X,Y,num_iterations,learning_rate,print_cost):  
69.     costs=[]  
70.     for i in range(num_iterations):  
71.         grads,cost=propagate(w,b,X,Y)  
72.         dw=grads['dw']  
73.         db=grads['db']  
74.     
75.         w=w-learning_rate*dw  
76.         b=b-learning_rate*db  
77.     
78.         #记录误差  
79.         if i % 100==0:  
80.             costs.append(cost)  
81.         if print_cost and i%100==0:  
82.             print('迭代次数：%i.误差值：%f' %(i,cost))  
83.     #组装数据  
84.     params={'w':w,'b':b}  
85.     return (params,costs)  
86.     
87. #建立预测函数  
88.     
89. def predict(w,b,X):  
90.     value=sigmod(np.dot(w.T,X)+b)  
91.     Y_prediction=(value>0.5)+0  
92.         
93.     ''''' 
94. 对于上一代码详解 
95. value>0.5是个判断语句，>0.5会返回True 
96. +0.是让布尔值转化成数字，1 
97.    
98. '''  
99.     return Y_prediction  
100.     
101.     
102. #下面是整合所有函数了  
103. def model(X_train,Y_train,X_test,Y_test,num_iterations=2000,learning_rate=0.01,print_cost=False):  
104.     #先调用X_train，Y_train，来训练处w，b  
105.     m=X_train.shape[1]  
106.     w,b=initialize(X_train.shape[0])  
107.     params,costs=optimize(w,b,X_train,Y_train,num_iterations,learning_rate,print_cost)  
108.     w,b=params['w'],params['b']  
109.     
110.     #计算预测值  
111.     Y_prediction_train=predict(w,b,X_train)  
112.     Y_prediction_test=predict(w,b,X_test)  
113.     
114.     #比较  
115.     print('TrainRightRate:',format(100-np.mean(np.abs(Y_prediction_train-Y_train))*100),'%')  
116.     print('TestRightRate:',format(100-np.mean(np.abs(Y_prediction_test-Y_test))*100),'%')  
117.         
118.     ''''' 
119. 上面代码详解 
120. abs（Y_p-T_r),此处两相比较，相同，预测对了，则详减为0，预测错了，则为1或者-1 
121. abs，全部取正 
122. mean，平均值，即有多少个+-1在所有数据中，即在所有数据中错误的个数/总数据 
123. 我要的是正确率，所以前面要用100来减 
124. '''  
125.     #数据组装  
126.     d={  
127.         'costs':costs,  
128.         'Y_prediction_train':Y_prediction_train,  
129.         'Y_prediction_test':Y_prediction_test,  
130.         'w':w,  
131.         'b':b,  
132.         'learning_rate':learning_rate,  
133.         'num_iterations':num_iterations}  
134.     return d  
135.     
136. #d=model(train_x,train_y,test_x,test_y,num_iterations=2000,learning_rate=0.005,print_cost=True)  
137.     
138.     
139. ''''' 
140. 上面就算是整个模型搭建完了，下面是可视化 
141. 表示迭代次数，学习率，与成本函数的关系 
142. '''  
143.     
144. learning_rate=[0.01,0.001,0.0001]  
145. models={}  
146. for i in learning_rate:  
147.     print ("learning rate is: " + str(i))  
148.     models[str(i)]=model(train_x,train_y,test_x,test_y,num_iterations=500,learning_rate=i)  
149.     print ('\n' + "-------------------------------------------------------" + '\n')  
150. for i in learning_rate:  
151.     plt.plot(np.squeeze(models[str(i)]['costs']),label=str(models[str(i)]["learning_rate"]))  
152. plt.ylabel('cost')  
153. plt.xlabel('iterations')  
154.     
155. legend = plt.legend(loc='upper center', shadow=True)  
156. frame = legend.get_frame()  
157. frame.set_facecolor('0.90')  
158. plt.show() 

 

代码笔记

1. 从另外一个文件中导入py文件中的某个函数

   import sys

   sys.path.append(r'path')

   from lr_utils import load_datasert

2. 记住X要组装成（n,m）矩阵，w是一个（n,1）的列向量

   有利于记住使用np.dot()时，哪个放前面，哪个放后面，也 有利于广播时是否需要转置的判断

3. 数据处理

   本例子中是将每个元/255，让[0,255],的数据计算，变成了[0,1]的数据计算，加快计算

   还有很多其他的数据处理方式，还没学到，多做多学

4. np.reshape(a,-1)中-1的妙用，只要把一个数组的行写出来了，列向量可以使用-1，让计算机自动计算分配，只要是负值就行
5. w-=learning_rate*dw 不知道为什么不能使用，需要常规操作，w=w-learning_rate*dw
6. A and B，两个判断，只要有一个是False，那整个语句就是错的，本例子，使用and来控制是否输出迭代次数与误差
7. 布尔值转数字 让布尔值'+0'就行了，numpy对于判断语句，也是并行运行的
8. 对于同类型的数据，多用字典dict组装，如梯度，初始值
9. np.squeeze()函数，将(5,1,1)转换成(5,)降维处理，有利于运行，也是可视化操作时，作为输入时，不可缺少的操作

   >>> a=np.random.randn(10000,1,1,1,1)

   >>> sys.getsizeof(a)

   80160

   >>> b=np.random.randn(10000)

   >>> sys.getsizeof(b)

   80096

10. 可视化操作中，参数解释：loc：选择把线型说明放在哪个地方，shadow，是否加营养

    frame.set_facecolor（'0.9'），给说明的地方加了框之后，再选择填充框的透明度

11. 使用'''作解释时，也需要遵循Python的缩进格式，否则会报错
12. 空一行 print('\n')