表示无向图的的数据类型

引言

最近我在读 Robert Sedgewick 和 Kevin Wayne 的经典著作《算法（第4版）》：

这本书第4章第1节讨论无向图，下面就是无向图的 API（英文版第522页）：

对于非稠密的无向图，标准表示是使用邻接表，将无向图的每个顶点的所有相邻顶点都保存在该顶点对应的元素所指向的一张链表中。所有的顶点保存在一个数组中，使用这个数组就可以快速访问给定顶点的邻接顶点列表。下面就是非稠密无向图的一个例子（英文版第525页）：

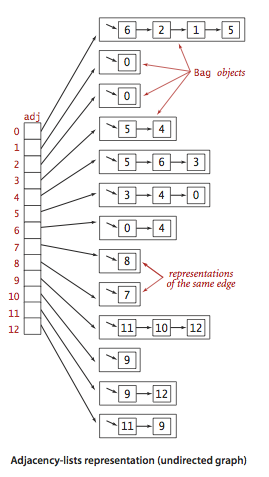
这种 Graph 的实现的性能有如下特点：

• 使用的空间和 V + E 成正比
• 添加一条边所需的时间为常数
• 遍历顶点 v 的所有相邻顶点所需的时间和 v 的度数成正比（处理每个相邻顶点所需的时间为常数）

对于这些操作，这样的特性已经是最优的了，已经可以满足图处理应用的需要。

Java 程序

下面就是 Graph.java 程序（英文版第526页）：

public class Graph
{
  private final int V;        // number of vertices
  private int E;              // number of edges
  private Bag<Integer>[] adj; // adjacency lists
  
  public Graph(int V)
  {
    this.V = V; this.E = 0;
    adj = (Bag<Integer>[]) new Bag[V]; // Create array of lists.
    for (int v = 0; v < V; v++)        // Initialize all lists
      adj[v] = new Bag<Integer>();     //   to empty.
  }

  public Graph(In in)
  {
    this(in.readInt());         // Read V and construct this graph.
    int E = in.readInt();       // Read E.
    for (int i = 0; i < E; i++)
    { // A an edge.
      int v = in.readInt();     // Read a vertex,
      int w = in.readInt();     //   read another vertex,
      addEdge(v, w);            //   and add edge connecting them.
    }
  }

  public int V() { return V; }
  public int E() { return E; }

  public void addEdge(int v, int w)
  {
    adj[v].add(w);  // Add w to v's list.
    adj[w].add(v);  // Add v to w's list.
    E++;
  }

  public Iterable<Integer> adj(int v)
  { return adj[v]; }

  public String toString()
  {
    StringBuilder s = new StringBuilder();
    String NEWLINE = System.getProperty("line.separator");
    s.append(V + " vertices, " + E + " edges" + NEWLINE);
    for (int v = 0; v < V; v++)
    {
      s.append(v + ": ");
      for (int w : adj[v]) s.append(w + " ");
      s.append(NEWLINE);
    }
    return s.toString();
  }

  public static void main(String[] args)
  {
    Graph G = new Graph(new In(args[0]));
    StdOut.println(G);
  }
}

在上述程序中：

• 第 3 行的字段表示该无向图的顶点数 V，这个值在构造函数中初始化后就不能修改了。
• 第 4 行的字段表示该无向图的边数 E 。
• 第 5 行的字段表示该无向图的邻接表数组。
• 第 7 至 13 行的 Graph 构造函数创建一幅含有 V 个顶点但没有边的无向图。
• 第 10 行创建邻接表数组，每个顶点都对应数组的一项，其元素就是该顶点的邻接表，这个邻接表使用 Bag 抽象数据类型来实现。
• Bag 数据类型请参见《算法（第4版）》1.3 节，该数据类型使得我们可以在常数时间内添加新的边或遍历任意顶点的所有相邻顶点。
• 由于 Java 语言固有的缺点，无法创建泛型数组，所以第 10 行中只能创建普通数组后强制转型为泛型数组。这导致在编译时出现警告信息。
• 由于 Java 语言固有的缺点，泛型的参数类型不能是原始数据类型，所以第 5、10、12 和 37 行的泛型的参数类型是 Integer，而不是 int 。这导致了一些性能损失。
• 第 15 至 25 行的构造函数从输入流生成无向图。输入流的内容首先是顶点数 V，接着是边数 E，然后是每条边的顶点。输入流的示例请参见引言中的 tinyG.txt 。表示输入流的 In 类型请参见《算法（第4版）》1.1 节。
• 第 30 至 35 行的 addEdge 方法添加一条连接 v 与 w 的边，其做法是将 w 添加到 v 的邻接表中并把 v 添加到 w 的邻接表中。因此，在这个数据结构中每条边都会出现两次。
• 第 40 至 52 行的 toString 方法返回该无向图的邻接表表示，首先是顶点数 V 和边数 E，然后是各顶点的邻接表。
• 第 54 至 58 行的 main 是测试用例。它从命令行参数获得输入流的名称。
• 第 56 行从输入流构造无向图。
• 第 57 行（隐式）调用 toString 方法输出该无向图。

编译和运行：

work$ javac Graph.java
注: Graph.java使用了未经检查或不安全的操作。
注: 有关详细信息, 请使用 -Xlint:unchecked 重新编译。
work$ java Graph tinyG.txt
13 vertices, 13 edges
0: 6 2 1 5 
1: 0 
2: 0 
3: 5 4 
4: 5 6 3 
5: 3 4 0 
6: 0 4 
7: 8 
8: 7 
9: 11 10 12 
10: 9 
11: 9 12 
12: 11 9 

这里的 tinyG.txt 文件的内容如下所示（内容和引言中的一样，列在这里是为了方便各位复制粘贴。引言中的是图片，无法复制粘贴）：

work$ cat tinyG.txt
13
13
0 5
4 3
0 1
9 12
6 4
5 4
0 2
11 12
9 10
0 6
7 8
9 11
5 3

C# 程序

将上一节的 Graph.java 翻译为 C# 程序，得到 Graph.cs ：

using System;
using System.Text;
using System.Collections.Generic;

namespace Skyiv
{
  public class Graph
  {
    public int V { get; private set; } // number of vertices
    public int E { get; private set; } // number of edges
    Stack<int>[] adj;                  // adjacency lists
    
    public Graph(int V)
    { Initialize(V); }
    
    public Graph(In @in)
    {
      Initialize(@in.ReadInt());  // Read V and construct this graph.
      int E = @in.ReadInt();      // Read E.
      for (var i = 0; i < E; i++)
      { // Add an edge.
        var v = @in.ReadInt();    // Read a vertex,
        var w = @in.ReadInt();    //   read another vertex,
        AddEdge(v, w);            //   and add edge connecting them.
      }
    }
    
    void Initialize(int V)
    {
      this.V = V;
      adj = new Stack<int>[V];     // Create array of lists.
      for (int v = 0; v < V; v++)  // Initialize all lists
        adj[v] = new Stack<int>(); //   to empty.
    }
    
    public void AddEdge(int v, int w)
    {
      adj[v].Push(w);  // Add w to v's list.
      adj[w].Push(v);  // Add v to w's list.
      E++;
    }
    
    public IEnumerable<int> Adj(int v)
    { return adj[v]; }
    
    public override string ToString()
    {
      var s = new StringBuilder();
      s.AppendLine(V + " vertices, " + E + " edges");
      for (var v = 0; v < V; v++)
      {
        s.Append(v + ": ");
        foreach (var w in Adj(v)) s.Append(w + " ");
        s.AppendLine();
      }
      return s.ToString();
    }
    
    static void Main(string[] args)
    {
      var G = new Graph(new In(args[0]));
      Console.Write(G);
    }
  }
}

上述 C# 程序基本上是 Java 程序的翻译：

• 第 9 至 10 行使用 C# 的属性代替 Java 字段，表示顶点数 V 和边数 E 。
• 第 11 行使用泛型的 Stack<int> 类型代替 Java 的 Bag<Integer> 类型，表示各顶点的邻接表。
• C# 语言没有上面说的 Java 语言的缺点，可以直接使用 int 类型作为泛型参数。
• 第 13 至 26 行的两个构造函数基本上是 Java 语言版本的翻译。
• 第 28 至 34 行的 Initialize 方法是 Java 语言版本第一个构造函数的翻译。
• 第 31 行创建邻接表数组，它没有 Java 语言的缺点，可以直接创建泛型数组，不用强制转型。
• 第 46 至 57 行的 ToString 方法是 Java 语言版本的 toString 方法的翻译。C# 语言的 StringBuilder 类有 AppendLine 方法，就不需要 Java 语言版本中的 NEWLINE 了。
• 其他各个方法也基本上是 Java 语言版本的对应翻译。

编译和运行的结果如下所示：

work$ dmcs Graph.cs In.cs
work$ mono Graph.exe tinyG.txt
13 vertices, 13 edges
0: 6 2 1 5 
1: 0 
2: 0 
3: 5 4 
4: 5 6 3 
5: 3 4 0 
6: 0 4 
7: 8 
8: 7 
9: 11 10 12 
10: 9 
11: 9 12 
12: 11 9 

可以看到，运行结果和 Java 程序一模一样。

Java 和 C# 程序的比较

前两节 Graph.java 和 Graph.cs 这两个程序是不是非常相像？还可以更像一点，在 Graph.java 使用了《算法（第4版）》作者写的 Bag 数据类型，这其实可以替换为 Java 标准库中的 Stack 数据类型。在 Graph.java 中：

• 把所有的 Bag 都替换为 Stack
• 把第 32 行和第 33 行的两个 add 替换为 push

这样修改后的 Java 程序运行结果不变。其实，诞生于 2000 年的 C# 语言受诞生于 1995 年的 Java 语言的影响非常大，并且利用其后发优势，继承 Java 语言的优点，抛弃 Java 的缺点。比如前面提到的 Java 语言在泛型方面的两个缺点（《算法（第4版）》这本书中也对这两个缺点引以为憾），在 C# 语言中就不在存在了。Java 语言要照顾以前写的代码，向前兼容，历史包袱太大了。Scala 语言是 Java 平台上的新兴语言，很有发展前途。不过我个人更看好 C# 语言，主要是用 C# 语言写程序。

加料的 C# 程序

在引言中的 Output for list-of-edges input 的图中，每条边出现第二次时被标记为红色，这是《算法（第4版）》的作者手工标记的，而不是程序的实际运行结果。如果我们的程序要做到这一点，可以在 Graph.cs 中作如下修改：

1. 在第 11 行之后增加一条语句（repeated 作为 Graph 类的字段，用于标记第二次出现的边）：

HashSet<Tuple<int, int>> repeated = new HashSet<Tuple<int, int>>();

2. 在第 40 行之后增加一条语句（在 AddEdge 方法中，将第二次出现的边标记为红色）：

repeated.Add(Tuple.Create(w, v));

3. 在第 58 行之后增加以下 Display 方法（将第二次出现的边使用红色显示）：

public void Display()
{
  var defaultColor = Console.ForegroundColor;
  Console.WriteLine("{0} vertices, {1} edges", V, E);
  for (var v = 0; v < V; v++)
  {
    Console.Write(v + ": ");
    foreach (var w in Adj(v))
    {
      var red = repeated.Contains(Tuple.Create(v, w));
      if (red) Console.ForegroundColor = ConsoleColor.Red;
      Console.Write(w + " ");
      if (red) Console.ForegroundColor = defaultColor;
    }
    Console.WriteLine();
  }
}

4. 将第 62 行的语句改为（在 Main 方法中，使用 Display 方法代替隐式的 ToString 方法）：

G.Display();

下面就是修改后的程序的运行结果：

读取输入的 C# 辅助程序

下面是前面用到的 In.cs 的源程序：

using System;
using System.IO;

namespace Skyiv
{
  public class In : IDisposable
  {
    static readonly byte[] BLANKS = { 9, 10, 13, 32 }; // tab,lf,cr,space
    static readonly byte EOF = 0; // assume '\0' not in input file
     
    byte[] buffer = new byte[64 * 1024];
    int current = 0, count = 0;
    Stream reader;

    public In() : this(Console.OpenStandardInput()) {}
    public In(string name) : this(File.OpenRead(name)) {}
    public In(Stream stream) { reader = stream; }

    byte ReadByte()
    {
      if (current >= count)
      {
        count = reader.Read(buffer, current = 0, buffer.Length);
        if (count == 0) return EOF;
      }
      return buffer[current++];
    }

    public int ReadInt()
    {
      var n = 0;
      var ok = false;
      for (byte b; (b = ReadByte()) != EOF; )
      {
        if (Array.IndexOf(BLANKS, b) >= 0)
          if (ok) break;
          else continue;
        n = n * 10 + (b - '0');
        ok = true;
      }
      return n;
    }

    public void Dispose()
    {
      if (reader != null) reader.Close();
    }
  }
}

这个程序来源于参考资料[7]。

运行环境

我们的程序是在 Arch Linux 64-bit 操作系统下运行的，Java 环境是 OpenJDK 1.7.0，.NET 环境是 Mono 3.0.6：

work$ uname -a
Linux m6100t 3.7.10-1-ARCH #1 SMP PREEMPT Thu Feb 28 09:50:17 CET 2013 x86_64 GNU/Linux
work$ java -version
java version "1.7.0_15"
OpenJDK Runtime Environment (IcedTea7 2.3.7) (ArchLinux build 7.u13_2.3.7-2-x86_64)
OpenJDK 64-Bit Server VM (build 23.7-b01, mixed mode)
work$ javac -version
javac 1.7.0_15
work$ echo $CLASSPATH
/home/ben/src/algs/stdlib.jar:/home/ben/src/algs/algs4.jar
work$ mono --version
Mono JIT compiler version 3.0.6 (tarball 2013年 03月 11日 星期一 11:54:36 CST)
Copyright (C) 2002-2012 Novell, Inc, Xamarin Inc and Contributors. www.mono-project.com
	TLS:           __thread
	SIGSEGV:       altstack
	Notifications: epoll
	Architecture:  amd64
	Disabled:      none
	Misc:          softdebug 
	LLVM:          supported, not enabled.
	GC:            Included Boehm (with typed GC and Parallel Mark)
work$ dmcs --version
Mono C# compiler version 3.0.6.0

注意，要编译和运行本文中 Java 程序，需要设置 CLASSPATH 环境变量，请见参考资料[3] 。

参考资料

1. 算法（第4版），[美] Robert Sedgewick, Kevin Wayne 著，谢路云译，人民邮电出版社，2012年10月第1版
2. 算法（英文版 第4版），[美] Robert Sedgewick, Kevin Wayne 著，人民邮电出版社，2012年3月第1版
3. Algorithms (Fourth Edition, Robert Sedgewick, Kevin Wayne): Java Algorithms and Clients
4. Algorithms (Fourth Edition, Robert Sedgewick, Kevin Wayne): Undirected Graphs
5. Wikipedia: Graph theory
6. Wikipedia: Adjacency list
7. 博客园：C# I/O 助手类