数据结构系列(3)之 伸展树
本文将主要讲述 BBST 家族的另一种相对奇特的树,伸展树;伸展树的相较于其他的 BBST,结构更加简单,因为伸展树不需要平衡因子、颜色等信息,他的节点就是 BST 的节点,同时他甚至没有时刻维护全树的平衡状态,却仍然能保持各项操作达到分摊 O(logn);
一、结构概述
伸展树的结构和二叉树完全相同,只是在实现上多了一步伸展;伸展树蕴含的主要思想就是数据访问的局部性,也就是说
- 刚刚访问过的节点,极有可能很快会再次访问;
- 下一次要访问的节点,极有可能就在刚被访问过的节点附近;
这一现象在我们生活正十分的常见,比如你的电脑,可能有几百G的资料,但是经常用的可能只有百分之一;所以伸展树的核心方法就是将刚刚操作过的节点移动到根位置,如图所示:

二、单层伸展
根据以上的描述你可能很快会想到,要想把底部的元素伸展至树根位置,只需要依次旋转其父节点即可;这样左的确可以,但是在极端情况下却可能会使时间复杂度上升至 O(n);如图所示:
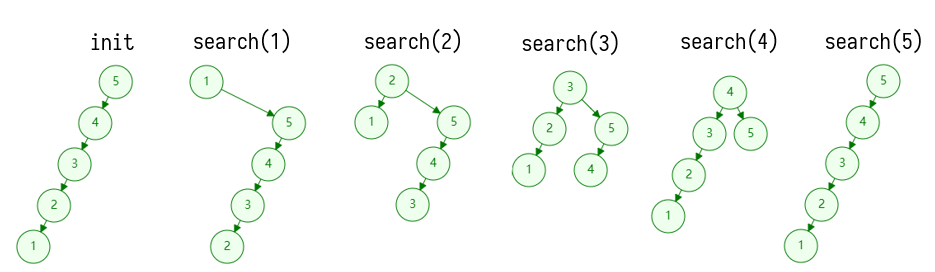
图中展示了二叉树的极端情况,即退化为了列表,然后依次访问末端元素,至所有元素都访问一遍后,发现又回到了初始状态,所以这种单层的伸展是万万不可取的;
三、双层伸展
而双层伸展则是根据其父亲节点和祖父节点的相对位置,进行相应的旋转。并分成以下分三类情况:
1. zig-zig/zag-zag
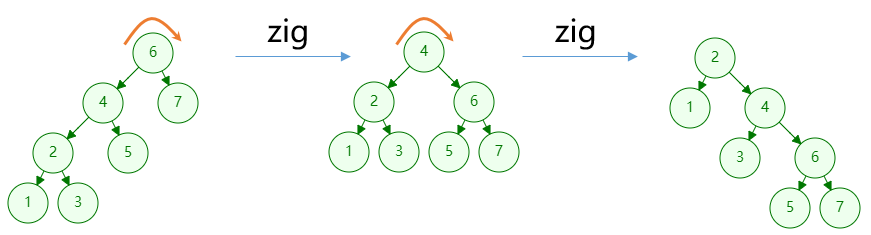
如图所示,当祖孙三代左倾或者右倾时,先旋转祖父节点再旋转父节点;
2. zig-zag/zag-zig

如图所示,当祖孙三代左倾、右倾交替时,先旋转父节点,使其转化为同为左倾或右倾,再旋转祖父节点;
3. zig/zag
当节点的深度为奇数时,则最后一次旋转仅为单层即可;
四、伸展算法
protected void splay(Node<T> node) {
// move node up until its root
while (node != root) {
// Zig step
Node<T> parent = node.parent;
if (parent.equals(root)) {
if (node.equals(parent.left)) {
rotateRight(parent);
} else if (node.equals(parent.right)) {
rotateLeft(parent);
}
break;
} else {
Node<T> grandParent = parent.parent;
boolean isLL = node.equals(parent.left) && parent.equals(grandParent.left);
boolean isRR = node.equals(parent.right) && parent.equals(grandParent.right);
boolean isRL = node.equals(parent.right) && parent.equals(grandParent.left);
boolean isLR = node.equals(parent.left) && parent.equals(grandParent.right);
// Zig zig step to the right
if (isLL) {
rotateRight(grandParent);
rotateRight(parent);
}
// Zig zig step to the left
else if (isRR) {
rotateLeft(grandParent);
rotateLeft(parent);
}
// Zig zag steps
else if (isRL) {
rotateLeft(parent);
rotateRight(grandParent);
} else if (isLR) {
rotateRight(parent);
rotateLeft(grandParent);
}
}
}
}
注意:这里仍然可以使用之前在 [AVL 树](https://www.cnblogs.com/sanzao/p/1046341 讲过的3+4重构,详情可以参考,6.html) 中讲过的 3+4重构;
五、查找
1. 查找成功
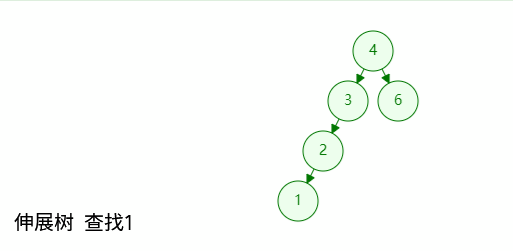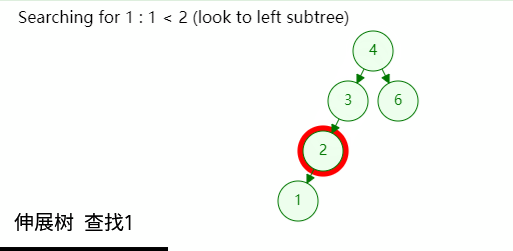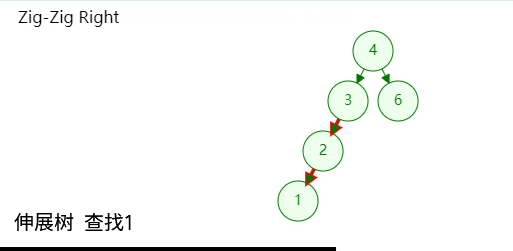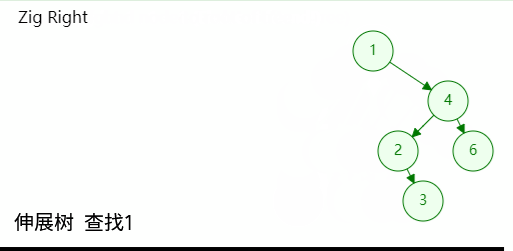
如图所示,查找成功的时候只需要将目标节点伸展到树根位置;
2. 查找失败

如图所示,查找失败的时候则需要将失败的前一个节点(也就是最接近目标的节点),伸展至树根位置;
3. 实现
@Override
public Node<T> search(T key) {
if (key == null) return null;
Node<T> u = super.binSearch(root, key);
splay(u);
return (key.compareTo(u.key) == 0) ? u : null;
}
// 查找最接近key的节点
public Node<T> binSearch(Node<T> v, T key) {
Node<T> u = v;
while (true) {
int comp = key.compareTo(u.getKey());
if (comp < 0)
if (u.left != null)
u = u.left;
else
return u; // 失败于左节点
else if (comp > 0)
if (u.right != null)
u = u.right;
else
return u; // 失败于右节点
else
return u; // 查找成功
}
}
六、插入
如图所示,插入也是同理,只需将最后插入的节点伸展至树根位置即可;
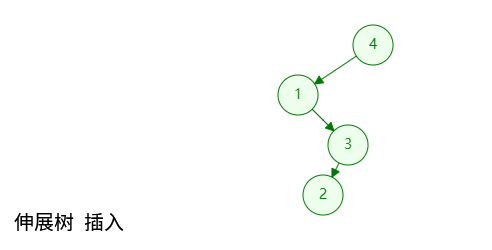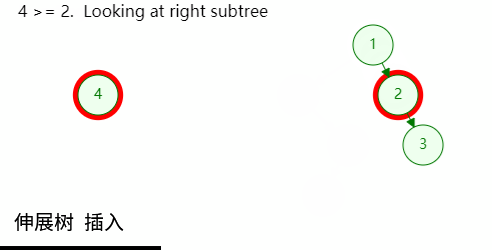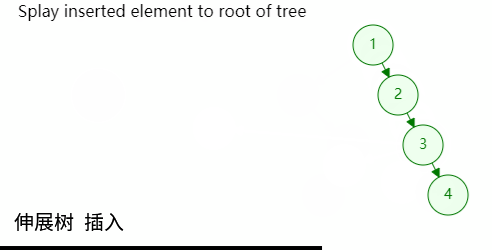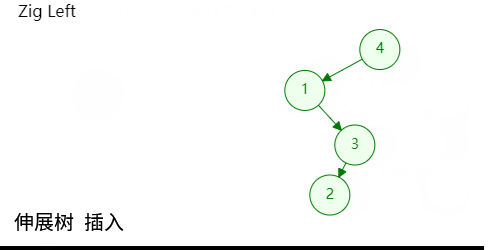
实现
@Override
public Node insert(int element) {
Node insertNode = super.insert(element);
splay(insertNode);
return insertNode;
}
七、删除
1. 单节点删除
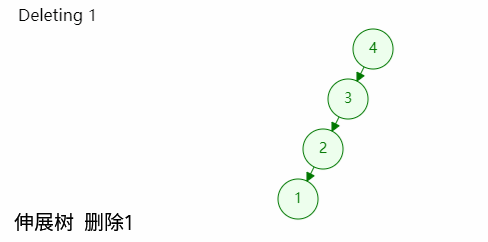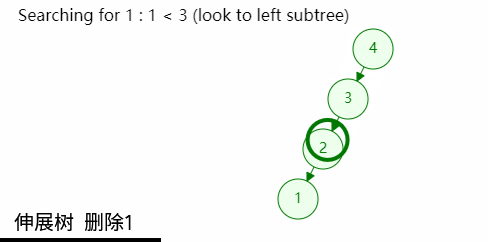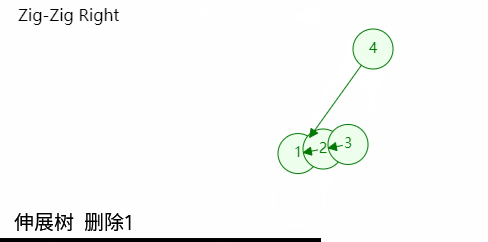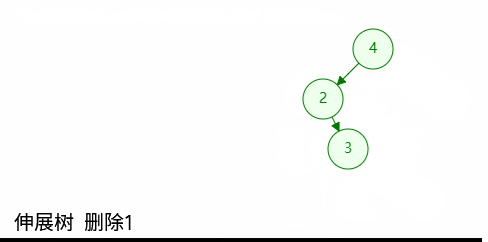
如图,经过一次查找后,目标节点已经移动至树根位置,若此时树根节点的左孩子或者右孩子为空,则可以直接删除,然后令其后代代替;
2. 双节点删除
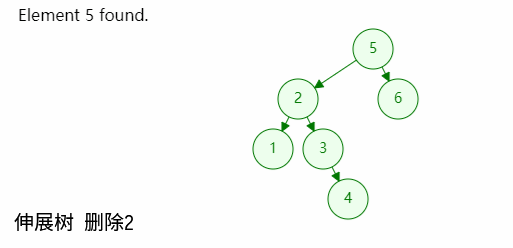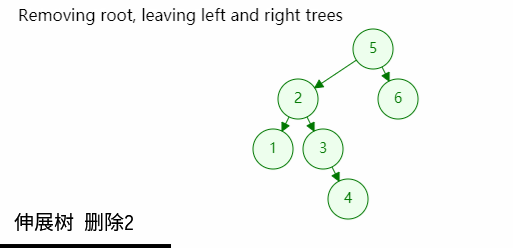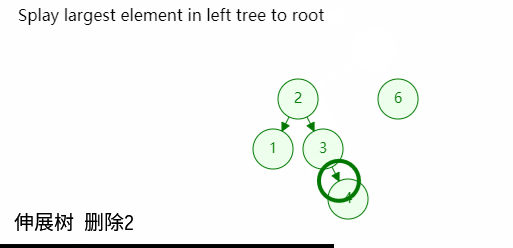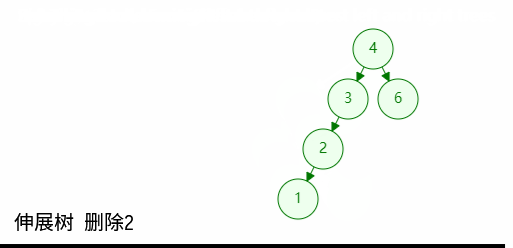
如图,当根节点同时拥有两个孩子的时候:
- 先删除根节点,元树分割为两个树
- 令左子树为根,再查找一次目标节点,此时左子树中最大的位置将伸展到树根位置;同时他的右孩子必然为空;
- 最后将分割出来的右子树接会树中即可;
3. 实现
public Node<T> delete2(T key) {
Node<T> node = search(key);
if (key.compareTo(node.key) != 0) {
return node;
}
// 查找成功,此时目标节点必然在树根处
if (root.left == null) {
root = root.right;
if (root != null) {
root.parent = null;
}
} else if (root.right == null) {
root = root.left;
if (root != null) {
root.parent = null;
}
} else {
Node<T> t1 = root.left;
Node<T> t2 = root.right;
t1.parent = null;
t2.parent = null;
root.left = null;
root.right = null;
root = t1;
// 查找必然失败,但是左子树中最大的节点已经伸展至树根位置,且右子树必然为空;(无相同节点)
search(key);
root.right = t2;
t2.parent = root;
}
return node;
}
同时这里也可以简单实现,即使用二叉树的删除,最后在伸展一次:
@Override
public Node<T> delete(T key) {
Node<T> deleteNode = super.delete(key);
splay(deleteNode);
return deleteNode;
}
总结
-
无需记录高度等信息,相对 AVL 树的实现而言,更简单一点,同时伸展树的各项操作均为 分摊
O(logn); -
不能杜绝单次最坏情况,所以不能用于效率敏感的场合;

