FP Tree算法原理总结

　　　　在Apriori算法原理总结中，我们对Apriori算法的原理做了总结。作为一个挖掘频繁项集的算法，Apriori算法需要多次扫描数据，I/O是很大的瓶颈。为了解决这个问题，FP Tree算法（也称FP Growth算法）采用了一些技巧，无论多少数据，只需要扫描两次数据集，因此提高了算法运行的效率。下面我们就对FP Tree算法做一个总结。

1. FP Tree数据结构

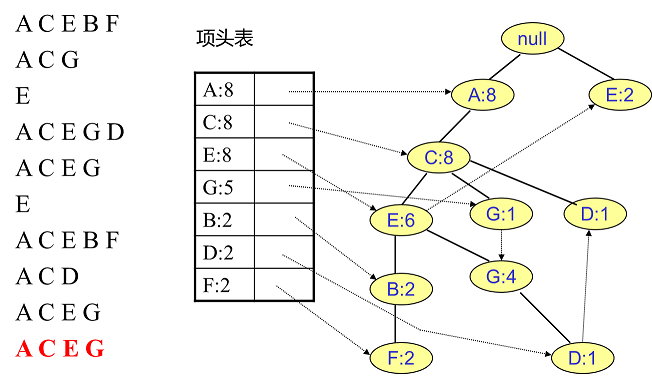
　　　　为了减少I/O次数，FP Tree算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分，如下图所示：

　　　　第一部分是一个项头表。里面记录了所有的1项频繁集出现的次数，按照次数降序排列。比如上图中B在所有10组数据中出现了8次，因此排在第一位，这部分好理解。第二部分是FP Tree，它将我们的原始数据集映射到了内存中的一颗FP树，这个FP树比较难理解，它是怎么建立的呢？这个我们后面再讲。第三部分是节点链表。所有项头表里的1项频繁集都是一个节点链表的头，它依次指向FP树中该1项频繁集出现的位置。这样做主要是方便项头表和FP Tree之间的联系查找和更新，也好理解。

　　　　下面我们讲项头表和FP树的建立过程。

2. 项头表的建立

　　　　FP树的建立需要首先依赖项头表的建立。首先我们看看怎么建立项头表。

　　　　我们第一次扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。接着第二次也是最后一次扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。

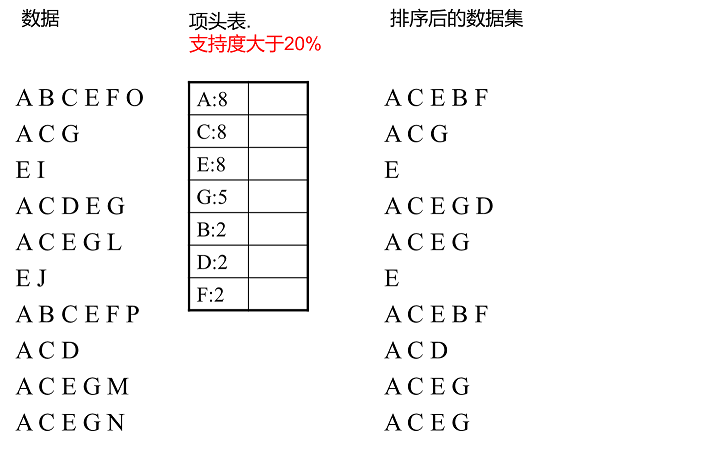
　　　　上面这段话很抽象，我们用下面这个例子来具体讲解。我们有10条数据，首先第一次扫描数据并对1项集计数，我们发现O，I，L，J，P，M, N都只出现一次，支持度低于20%的阈值，因此他们不会出现在下面的项头表中。剩下的A,C,E,G,B,D,F按照支持度的大小降序排列，组成了我们的项头表。

　　　　接着我们第二次扫描数据，对于每条数据剔除非频繁1项集，并按照支持度降序排列。比如数据项ABCEFO，里面O是非频繁1项集，因此被剔除，只剩下了ABCEF。按照支持度的顺序排序，它变成了ACEBF。其他的数据项以此类推。为什么要将原始数据集里的频繁1项数据项进行排序呢？这是为了我们后面的FP树的建立时，可以尽可能的共用祖先节点。

　　　　通过两次扫描，项头表已经建立，排序后的数据集也已经得到了，下面我们再看看怎么建立FP树。

3. FP Tree的建立

　　　　有了项头表和排序后的数据集，我们就可以开始FP树的建立了。开始时FP树没有数据，建立FP树时我们一条条的读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。

　　　　似乎也很抽象，我们还是用第二节的例子来描述。

　　　　首先，我们插入第一条数据ACEBF，如下图所示。此时FP树没有节点，因此ACEBF是一个独立的路径，所有节点计数为1, 项头表通过节点链表链接上对应的新增节点。

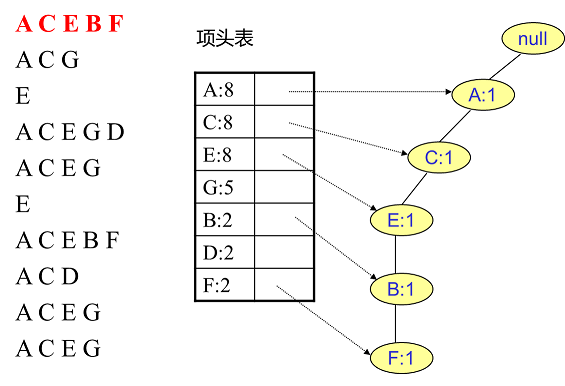
　　　　接着我们插入数据ACG，如下图所示。由于ACG和现有的FP树可以有共有的祖先节点序列AC，因此只需要增加一个新节点G，将新节点G的计数记为1。同时A和C的计数加1成为2。当然，对应的G节点的节点链表要更新

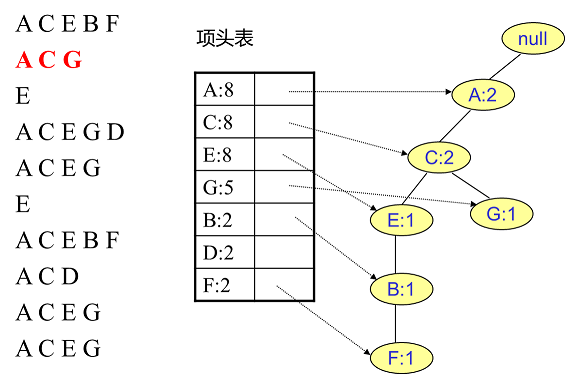
　　　　同样的办法可以更新后面8条数据，如下8张图。由于原理类似，这里就不多文字讲解了，大家可以自己去尝试插入并进行理解对比。相信如果大家自己可以独立的插入这10条数据，那么FP树建立的过程就没有什么难度了。

 

 

 

 

 

 

 

 

 

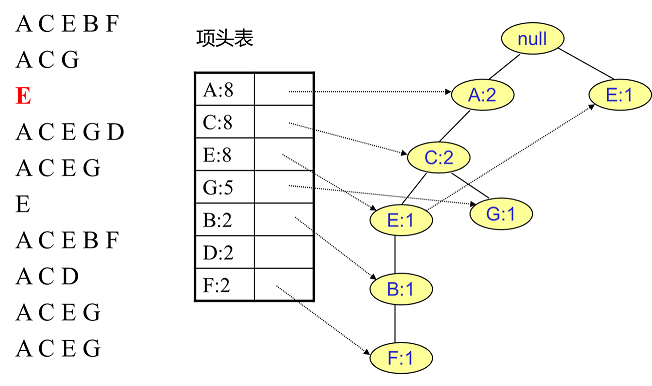
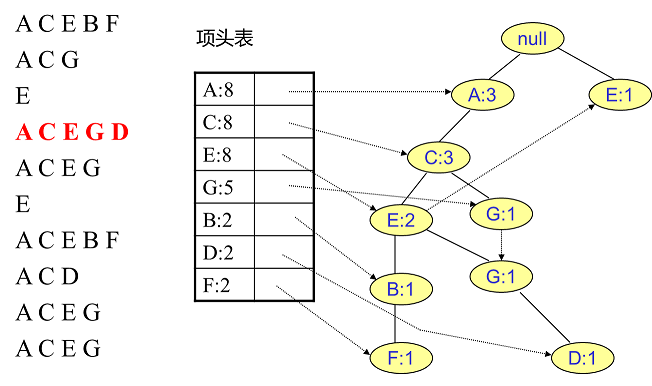
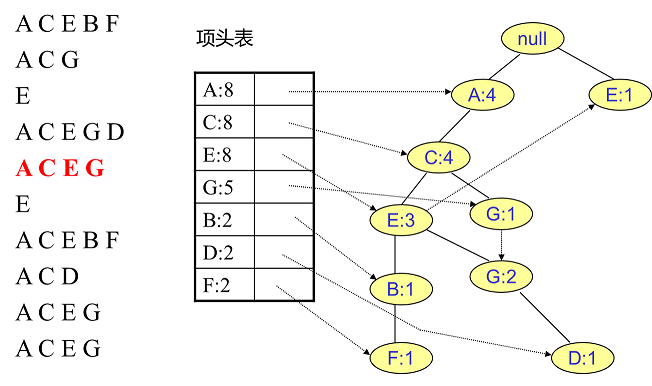
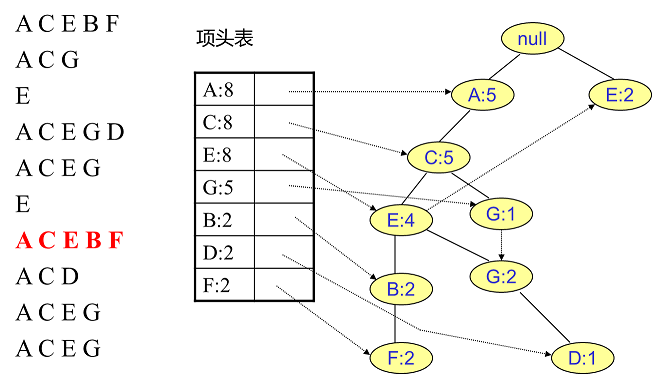
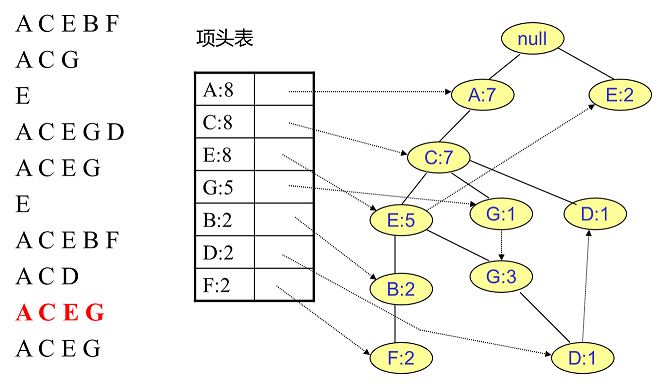
4. FP Tree的挖掘

　　　　我们辛辛苦苦，终于把FP树建立起来了，那么怎么去挖掘频繁项集呢？看着这个FP树，似乎还是不知道怎么下手。下面我们讲如何从FP树里挖掘频繁项集。得到了FP树和项头表以及节点链表，我们首先要从项头表的底部项依次向上挖掘。对于项头表对应于FP树的每一项，我们要找到它的条件模式基。所谓条件模式基是以我们要挖掘的节点作为叶子节点所对应的FP子树。得到这个FP子树，我们将子树中每个节点的的计数设置为叶子节点的计数，并删除计数低于支持度的节点。从这个条件模式基，我们就可以递归挖掘得到频繁项集了。

　　　　实在太抽象了，之前我看到这也是一团雾水。还是以上面的例子来讲解。我们看看先从最底下的F节点开始，我们先来寻找F节点的条件模式基，由于F在FP树中只有一个节点，因此候选就只有下图左所示的一条路径，对应{A:8,C:8,E:6,B:2, F:2}。我们接着将所有的祖先节点计数设置为叶子节点的计数，即FP子树变成{A:2,C:2,E:2,B:2, F:2}。一般我们的条件模式基可以不写叶子节点，因此最终的F的条件模式基如下图右所示。

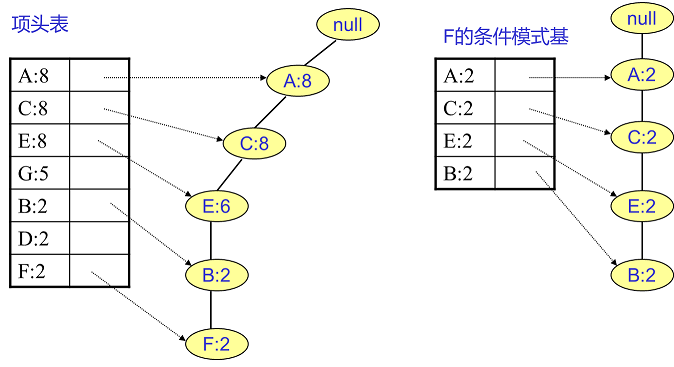
　　　　通过它，我们很容易得到F的频繁2项集为{A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,F:2}，{A:2,E:2,F:2},...还有一些频繁三项集，就不写了。当然一直递归下去，最大的频繁项集为频繁5项集，为{A:2,C:2,E:2,B:2,F:2}

　　　　F挖掘完了，我们开始挖掘D节点。D节点比F节点复杂一些，因为它有两个叶子节点，因此首先得到的FP子树如下图左。我们接着将所有的祖先节点计数设置为叶子节点的计数，即变成{A:2, C:2,E:1 G:1,D:1, D:1}此时E节点和G节点由于在条件模式基里面的支持度低于阈值，被我们删除，最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2, C:2}。通过它，我们很容易得到D的频繁2项集为{A:2,D:2}, {C:2,D:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集。

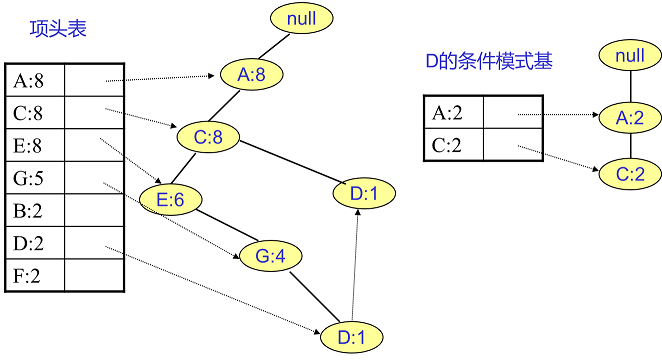
　　　　同样的方法可以得到B的条件模式基如下图右边，递归挖掘到B的最大频繁项集为频繁4项集{A:2, C:2, E:2,B:2}。

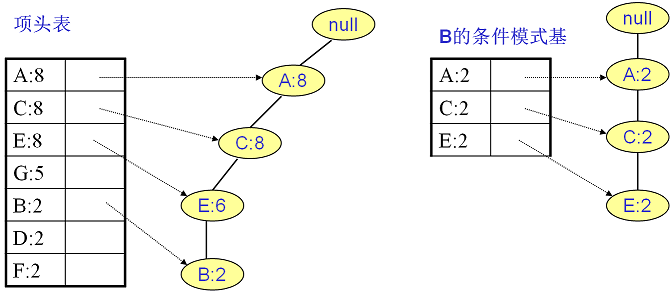
　　　　继续挖掘G的频繁项集，挖掘到的G的条件模式基如下图右边，递归挖掘到G的最大频繁项集为频繁4项集{A:5, C:5, E:4,G:4}。

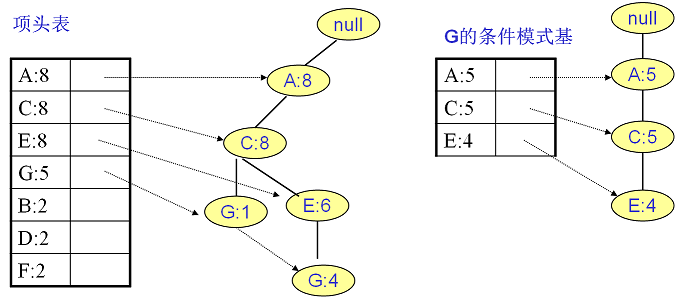
　　　　E的条件模式基如下图右边，递归挖掘到E的最大频繁项集为频繁3项集{A:6, C:6, E:6}。

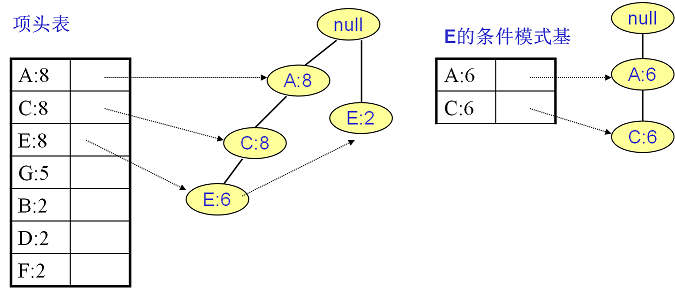
　　　　C的条件模式基如下图右边，递归挖掘到C的最大频繁项集为频繁2项集{A:8, C:8}。

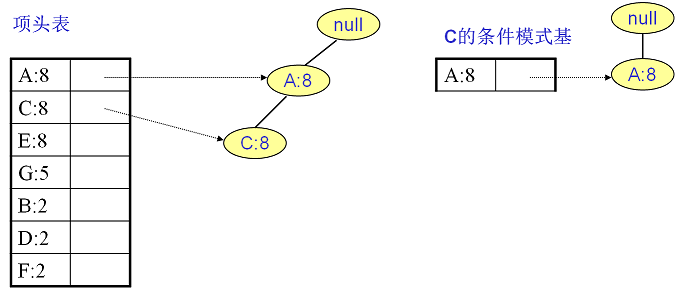
　　　　至于A，由于它的条件模式基为空，因此可以不用去挖掘了。

　　　　至此我们得到了所有的频繁项集，如果我们只是要最大的频繁K项集，从上面的分析可以看到，最大的频繁项集为5项集。包括{A:2, C:2, E:2,B:2,F:2}。

　　　　通过上面的流程，相信大家对FP Tree的挖掘频繁项集的过程也很熟悉了。

5. FP Tree算法归纳

　　　　这里我们对FP Tree算法流程做一个归纳。FP Tree算法包括以下几步：

　　　　1）扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。

　　　　2）扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。

　　　　3）读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。

　　　　4）从项头表的底部项依次向上找到项头表项对应的条件模式基。从条件模式基递归挖掘得到项头表项项的频繁项集（可以参见第4节对F的条件模式基的频繁二项集到频繁5五项集的挖掘）。

　　　　5）如果不限制频繁项集的项数，则返回步骤4所有的频繁项集，否则只返回满足项数要求的频繁项集。

6. FP tree算法总结

　　　　FP Tree算法改进了Apriori算法的I/O瓶颈，巧妙的利用了树结构，这让我们想起了BIRCH聚类，BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。

　　　　在实践中，FP Tree算法是可以用于生产环境的关联算法，而Apriori算法则做为先驱，起着关联算法指明灯的作用。除了FP Tree，像GSP，CBA之类的算法都是Apriori派系的。

 

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）