斐波那契堆

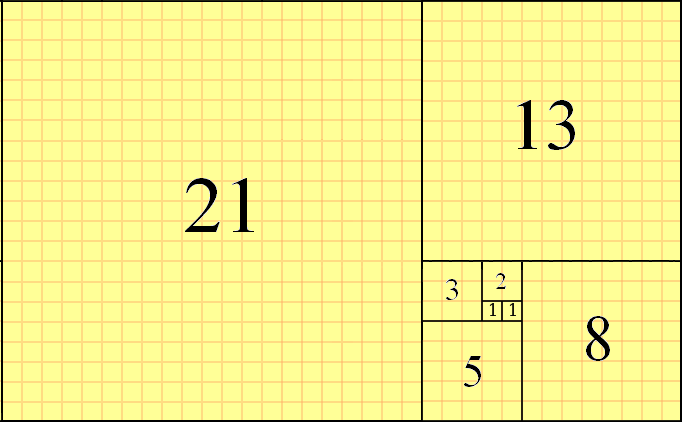
在计算机科学中，斐波那契堆是由树的集合所组成的堆数据结构。它比二项堆的平摊运行时间更好。斐波那契堆的名字来自于斐波那契数列，这些数列被用来做运行时间分析。

求最小值(find-mininum), 插入(insert), 降低元素值(decrease-key)和合并(merge/union)可以在常数平摊时间内完成。删除(delete)和删除最小值(delete minimun)可以在O(log n)平摊时间内完成。

在优先队列(priority queues)中使用斐波那契堆可以提升重要算法的渐进运行时间，例如Dijkstra算法，该算法用来计算一个图中两个结点的最短的距离。

斐波那契堆是由一些树的集合所组成，其中每一棵树都满足最小堆(minimum-heap)的属性，也就是说树中每个子结点的值都大于或者等于其父结点的值，而最小值则处在根结点上。

与二项堆不同，斐波那契堆中的树更加灵活，没有规定的形状，在极端情况下，堆中每个元素都是一棵单独的树。这种灵活性使得一些操作可以以“偷懒”的方式来执行，而“剩下”的工作将推迟到后面的操作中来完成。比如堆的合并仅仅将由树所组成的链表链接起来，而降低元素值(decrease key)有时直接从父结点中剪断而形成一棵新树。

下面给出斐波那契堆中关键的量值：

$degree[x]:$ 表示结点x的子结点个数

$mark[x]:$ 一个结点是否被marked了（当执行decrease key操作时会用到）

$t(H):$ 表示堆中树的个数

$m(H):$ 表示被marked的结点数量

$\Phi(H)=t(H)+2m(H):$ 表示势函数

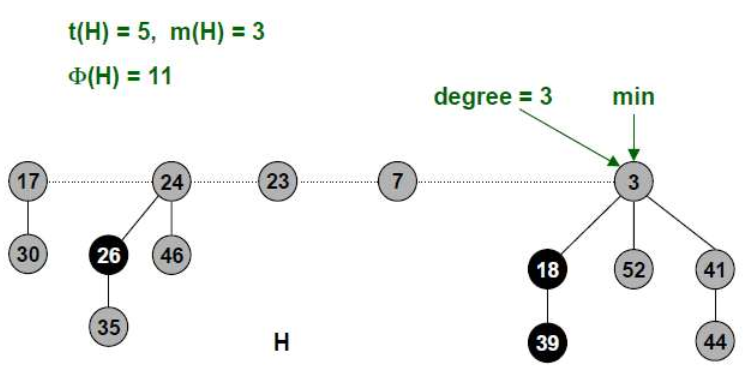
如下图所示：

从图中可以看出，一共有5棵树，即$t(H)=5$，最小值的指针指向元素值为3的根结点，在这棵包含最小值的树中，根结点有3个子结点，所以其degree等于3，整个斐波那契堆用 H 来表示。其中黑色表示被marked了，灰色表示没有被marked，所以$m(H)=3$，势函数 $\Phi(H)=t(H)+2m(H)=5+2*3=11$

 

关于具体的插入，合并，求最小值，降低元素值，以及删除操作可以找到很多资料，就不再重复了，可以参见：

http://www.cse.yorku.ca/~aaw/Jason/FibonacciHeapAnimation.html

http://gdeepak.com/IADSA/L22binomialfibonacciheaps.pdf

 

下面来看看“斐波那契堆”的名字是怎么来的，在 decrease key 的操作中，假设一个结点P的元素值为A，现在要将其降低为B，其父结点的值为C，则遵循这样的规则：

1、若B>=C, 则直接将A替换为B即可

2、若B<C, 结点P的父结点是根结点，则直接将结点P从根结点处剪断，形成一棵新树

3、若B<C, 结点P的父结点不是根结点，则将结点P从父结点处剪断，形成一棵新树，然后将父结点设置为marked

4、若B<C, 并且父结点已经被marked了，则不仅要将结点P从父结点处剪断，而且依次往上递归将被marked的父结点也从其父结点处剪断，直到碰到一个父结点没有被marked，或者碰到根结点为止

 

由上面的规则可以得到，只能将父结点下面的一个子结点剪断并形成一颗新树，此时父结点已经被marked了，如果再执行一次 decrease key 操作，并且需要从父结点处剪断，那么此时父结点本身也将被剪断，同时父结点的父结点的 degree 将变为 degree -1 ，所以在保证父结点 degree 不发生改变的情况下，子结点从父结点处剪断的操作只能执行一次，这样对于一个给定的结点，在其 degree 不发生改变的情况下，子结点的个数（加上根结点）有一个最小值，这些最小值满足斐波那契数列，如下图所示：

 

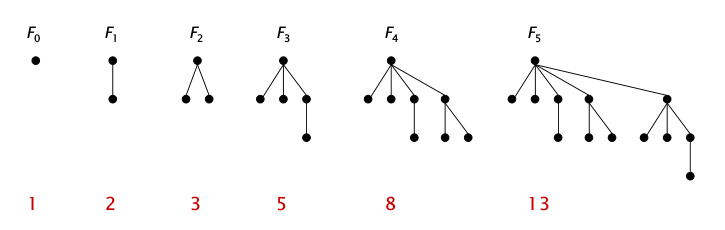
 从图中可以看出，第一棵树的 degree 为0，结点数目为1，第二棵树的 degree 为1，结点数目为2，只有一个子结点，此时如果执行 decrease key 操作，并且要将子结点从父结点处剪断，那么这棵树的根结点就没有子结点了，也就是说 degree 变成0了，此时就与第一棵的情况相同了，第三棵树同理可以得出。而 degree 从1开始一直往下，树的结点个数就形成了斐波那契数列，多么美妙啊，其中 degree=k 的结点个数为 $F_{k+2}$, 表示斐波那契数列中的第k+2项。

 

本文内容摘自维基百科：https://en.wikipedia.org/wiki/Fibonacci_heap