理论物理极础之插播数学2：积分

“乔治，我干事喜欢反着来。微分能反着来吗？”
“当然可以，莱尼，那就是积分。”

积分

微分处理的是变化率。积分做的是把许许多多微小的增量加起来求和。乍一看，微分与积分毫无关系，其实它们密切相关。

我们先画一个函数\(f(t)\)的图，如图1所示。

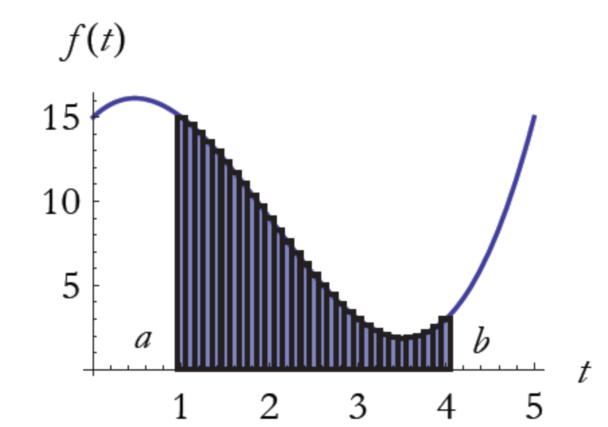
积分的中心问题是计算函数\(f(t)\)曲线下面的面积。为了使这个问题显得更清楚，我们考虑一段函数，如\(t=a\)和\(t=b\)之间的函数，选取的自变量这两个值称为积分限。我们要计算图2中阴影部分的面积。

要计算这个面积，我们把阴影部分分成很多很多纤薄的矩形（如图3），把这些小矩形的面积加起来，就是我们要求的面积。

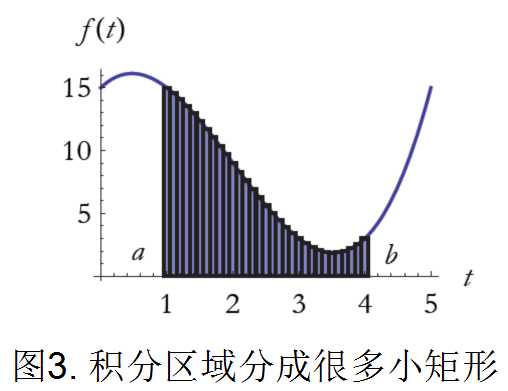
当然，这样得到的是近似结果，但是，当矩形的宽度趋于0，我们将得到准确结果。下面说一下计算步骤。第一步，把\(t=a\)和\(t=b\)之间的区域分成\(N\)个次区域，每个次区域的宽度为\(\Delta t\)。对于某个\(t\)处的小矩形，宽为\(\Delta t\)，高为此处的函数值\(f(t)\)，于是可得此处小矩形的面积为

\[\delta A =f(t)\Delta t \]

把所有的这些小矩形的面积加起来，就得到要求的阴影部分面积的近似值，

\[A =\sum_i f(t_i)\Delta t \]

其中的大写希腊字母\(\Sigma\)表示求和，即把一系列用\(i\)标记的值加起来。比如\(N=3\)，就有

\[A =\sum_i f(t_i)\Delta t=f(t_1)\Delta t+f(t_2)\Delta t+f(t_3)\Delta t \]

这里\(t_i\)表示第\(i\)个小矩形在\(t\)轴上的位置。

\(\Delta t\)趋于0，小矩形数目\(N\)趋于无穷，求出此时小矩形面积和的极限，此即为要求的面积的准确值，也即是\(f(t)\)的定积分的定义，写为下式：

\[A =\lim_{\Delta t \rightarrow 0}\sum_i f(t_i)\Delta t=\int_a^b f(t)dt \]

积分符号\(\int\)取代了求和符号，\(dt\)取代了\(\Delta t\)，积分符号里面的函数\(f(t)\)称为被积函数。

把上式中的\(b\)，换成\(T\)，得到这样一个积分，

\[\int_a^T f(t)dt \]

把\(T\)看成一个变量，上式这个积分就是变量\(T\)函数（注意不是\(t\)的函数）：

\[F(T)=\int_a^T f(t)dt \]

由一个给定的函数\(f(t)\)，定义出一个新的函数\(F(T)\)。前面的\(a\)也是可以变的，这里我们不考虑这种情况。这个新的函数\(F(T)\)称为\(f(t)\)的不定积分。称为不定积分，因为我们不是从一个固定值积分到另一个固定值，而是积分到另一个变量。对于不定积分，我们通常不写上下限，写为如下形式：
\begin{equation}F(t)=\int f(t)dt\label{eq:infd}\end{equation}

微分和积分之间有深刻联系，如果\(F(t)=\int f(t)dt\)，则有

\[f(t)=\frac{dF(t)}{dt} \]

这个联系就叫做微积分基本定理，下面我们说明一下这个结果的由来。变量\(T\)有个小的增量，从\(T\)变到\(T+\Delta t\)，于是有个新的积分，

\[F(T+\Delta t)=\int_a^{T+\Delta t} f(t)dt \]

即在图3阴影部分\(t=T\)处新加了一块宽为\(\Delta t\)矩形，于是差\(F(T+\Delta t)-F(T)\)即为多出来的这块小矩形的面积，

\[F(T+\Delta t)-F(T)=f(T)\Delta t \]

两边除以\(\Delta t\)，

\[\frac{F(T+\Delta t)-F(T)}{\Delta t}=f(T) \]

取极限\(\Delta t \rightarrow 0\)，有：

\[\lim_{\Delta t \rightarrow 0}\frac{F(T+\Delta t)-F(T)}{\Delta t}=\frac{dF}{dT}=f(T) \]

换一下变量的符号，则有

\[\frac{dF(t)}{dt}=f(t) \]

这说明，积分和微分是逆运算，积分的导数即原被积函数。

知道\(F(t)\)的导数是\(f(t)\)就能完全确定\(F(t)\)吗？还不能完全确定，因为\(F(t)\)加上一个常数不改变它的导数。给定一个函数\(f(t)\)，它的不定积分的函数形式是不定的，如果\(F(t)\)是\(f(t)\)的不定积分，\(F(t)\)加上任意常数之后，\(F(t)+C\)也是\(f(t)\)的不定积分。

下面我们说明一下微积分基本定理的应用。比如我们计算函数\(f(t)=t^n\)的积分，

\[F(t)=\int f(t)dt \]

根据微积分基本定理，有

\[f(t)=\frac{dF(t)}{dt} \]

即

\[t^n=\frac{dF(t)}{dt} \]

现在的任务就是找到一个函数\(F(t)\)，它的导数是\(t^n\)，这不是难事。

我们在上一章就已经知道，

\[\frac{d(t^m)}{dt}=mt^{m-1} \]

令\(m=n+1\)，则有

\[\frac{d(t^{n+1})}{dt}=(n+1)t^n \]

两边除以\(n+1\)，有

\[\frac{d(t^{n+1}/n+1)}{dt}=t^n \]

因此，\(t^n\)是\(\frac{t^{n+1}}{n+1}\)的导数，所以，

\[F(t)=\int t^ndt=\frac{t^{n+1}}{n+1} \]

再加上任意的常数，就得到\(t^n\)的不定积分，

\[\int t^ndt=\frac{t^{n+1}}{n+1}+C \]

积分常数\(C\)需要其他的条件来确定。

出现这个任意的常数是因为积分的一个积分限没有确定。如果我们选定另一个积分限，即前述的\(a\)，由\(a\)就可以确定常数\(C\)。考虑积分

\[\int_a^Tf(t)dt \]

当两个积分限为同一点，即 \(T=a\)，积分必为0，由此可确定积分常数\(C\)。

一般情形下的微积分基本定理写为如下形式：
\begin{equation}\int_a^b f(t)dt=F(t)\big |_a^b=F(b)-F(a)\label{eq:def}\end{equation}
另外一个表述方式是
\begin{equation}\int \frac{df}{dt}dt=f(t)+C\label{eq:const}\end{equation}
即对函数的导数积分得到原来的函数（加上一个任意常数）。

以下是几个有用的积分公式：

\[\int C dt=Ct+C'$$ （注：原文漏掉第二个常数$C'$） $$\int Cf(t)dt=C \int f(t)dt\]

\[\int t dt=\frac{t^2}{2}+C \]

\[\int t^2 dt=\frac{t^3}{3}+C \]

\[\int t^ndt=\frac{t^{n+1}}{n+1}+C \]

\[\int \sin t dt =-\cos t +C \]

\[\int \cos t dt =\sin t +C \]

\[\int e^t dt = e^t +C \]

\[\int \frac{dt}{t} = \ln t +C$$ （注：原文漏掉常数$C$） $$\int [f(t) \pm g(t)]dt = \int f(t)dt \pm \int g(t) dt \]

练习1：求下列函数的不定积分：$$f(t)=t^4$$ $$f(t)=\cos t$$ $$f(t)=t^2-a$$

练习2：取积分限分别为\(t=0\)和\(t=T\)，应用微积分基本定理重新计算练习1中的积分

练习3：把练习1中的函数视为一个粒子的加速度的表达式，积分一次，得到粒子的速度，再积分一次，得到粒子的轨迹。wom我们取\(t\)为积分限，把函数的哑变量改为\(t'\)，将函数从\(t'0\)积分到\(t'=t\)，$$v(t)=\int_0^t t'^4 dt'$$ $$v(t)=\int_0^t \cos t' dt'$$ $$v(t)=\int_0^t (t'^2-a) dt'$$

分部积分

计算积分可以查表，或者用数学软件\(Mathematica\)。如果不得不手算，有个古老的技巧，非常有用，这就是分部积分。我们曾在上一章讲过两个函数的积的导数：

\[\frac{d[f(x)g(x)]}{dx}=f(x)\frac{dg(x)}{dx}+g(x)\frac{df(x)}{dx} \]

对上式两边进行积分，从\(x=a\)积到\(x=b\)，

\[\int \frac{d[f(x)g(x)]}{dx}dx=\int f(x)\frac{dg(x)}{dx} dx + \int g(x)\frac{df(x)}{dx} dx \]

上式的左边比较容易，函数导数的积分是函数本身，即上式的左边为

\[f(b)g(b)-f(a)g(a) \]

常写为如下形式：

\[f(x)g(x)\vert_a^b \]

现在把右边其中一项移到左边，
\begin{equation}f(x)g(x)|_a^b-\int f(x)\frac{dg(x)}{dx} dx=\int g(x)\frac{df(x)}{dx} dx\label{eq:part}\end{equation}

现在考虑计算一个积分，被积函数恰好是一个函数\(f(x)\)与另外一个函数\(g(x)\)的导数的积，即方程(\ref{eq:part})右边的形式，如果直接积分没办法算，可以转换成方程(\ref{eq:part})左边的形式，如果运气好，左边的积分\(\int f(x)\frac{dg(x)}{dx} dx\)我们会算，那么方程(\ref{eq:part})右边的积分也就算出来了。

下面我们举个例子。比如计算如下积分：

\[\int_0^{\pi/2}x\cos x dx \]

注意到

\[\cos x = \frac{d\sin x}{dx}$$，于是要求的积分变成 $$\int_0^{\pi/2}x \frac{d\sin x}{dx} dx\]

根据方程(\ref{eq:part})，上式结果为：

\begin{equation}\notag x \sin x \vert_0^{\pi/2}-\int_0^{\pi/2}\frac{dx}{dx}\sin x dx\end{equation}

也即

\begin{equation}\notag x\sin x|_0^{{\pi/2}-\int_0}\sin x dx\end{equation}

\(\int\_0^{\pi/2}\sin x dx\)我们会算，那么剩下的事情比较容易了，请自己完成。

练习4：完成积分\(\int_0^{\pi/2}x\cos x dx\)的计算

你可能会问，分部积分这个技巧很常用吗？答案是：很常用，但不是每次都好用，看运气了。