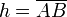公告

基本函数

如右图，当平面上的三点A、B、C的连线， $\overline{A B}$ 、 $\overline{B C}$ 、 $\overline{A C}$ ，构成一个直角三角形，其中 ${\angle ACB}$ 为直角。对于 $\overline{A B}$ 与 $\overline{A C}$ 的夹角 ${\angle BAC}$ 而言：

对边（opposite）

$a = \overline{B C}$

邻边（adjacent）

$b = \overline{A C}$

斜边（hypotenuse）

$h = \overline{A B}$

函数	英语	简写	定义	关系
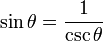正弦	Sine	sin	$\frac {a} {h}$	$\sin \theta = \frac{1}{\csc \theta}$
余弦	Cosine	cos	$\frac {b} {h}$	$\cos \theta = \frac{1}{\sec \theta}\,$
正切	Tangent	tan	$\frac {a} {b}$	$\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{1}{\cot \theta}$
余切	Cotangent	cot	$\frac {b} {a}$	$\cot \theta = \frac{\cos \theta}{\sin \theta} = \frac{1}{\tan \theta}$
正割	Secant	sec	$\frac {h} {b}$	$\sec \theta = \frac{1}{\cos \theta}$
余割	Cosecant	csc	$\frac {h} {a}$	$\csc \theta = \frac{1}{\sin \theta}$

注：中国大陆早期教科书中多将正切、余切写作tg，ctg，现已废弃不用。

另见：三角恒等式#基本关系

[编辑]罕见函数

除了上述六个基本函数，历史上还有下列几个罕见的函数：

正矢	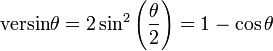$\textrm{versin} \theta = 2\sin^2\left(\frac{\theta}{2}\right) = 1 - \cos \theta \,$
	$\textrm{vercosin} \theta = 2\cos^2\left(\frac{\theta}{2}\right) = 1 + \cos \theta \,$
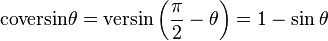余矢	$\textrm{coversin} \theta = \textrm{versin}\left(\frac{\pi}{2} - \theta\right) = 1 - \sin \theta \,$
	$\textrm{covercosin} \theta = \textrm{vercosin}\left(\frac{\pi}{2} - \theta\right) = 1 + \sin \theta \,$
半正矢	$\textrm{haversin} \theta = \frac {\textrm{versin} \theta} {2} = \frac{1 - \cos \theta}{2} \,$
	$\textrm{havercosin} \theta = \frac {\textrm{vercosin} \theta} {2} = \frac{1 + \cos \theta}{2} \,$
半余矢	$\textrm{hacoversin} \theta = \frac {\textrm{coversin} \theta} {2} = \frac{1 - \sin \theta}{2} \,$
	$\textrm{hacovercosin} \theta = \frac {\textrm{covercosin} \theta} {2} = \frac{1 + \sin \theta}{2} \,$
外正割	$\textrm{exsec} \theta = \sec \theta - 1 \,$
外余割	$\textrm{excsc} \theta = \textrm{exsec}(\frac{\pi}{2} - \theta) = \csc \theta - 1 \!$

[编辑]历史

早期对于三角函数的研究可以追溯到古代，现今使用的三角函数发展于欧洲的中世纪时期。Sin和Cos的使用最早可以追溯到印度笈多王朝的天文学时期，然后经由梵文翻译成阿拉伯文，再由阿拉伯文翻译成拉丁文。

随着认识到相似三角形在它们的边之间保持相同的比率，就有了在三角形的边的长度和三角形的角之间应当有某种标准的对应的想法。就是说对于任何相似三角形，（比如）斜边和剩下的两个边的比率都是相同的。如果斜边变为两倍长，其他边也要变为两倍长。三角函数表达的就是这些比率。

研究三角函数的有伊兹尼克的喜帕恰斯（公元前180－125年）、埃及的托勒密（公元90－180年）、阿里亚哈塔（公元476－550年）、伐罗诃密希罗、婆罗摩笈多、花拉子密、阿布·瓦法、欧玛尔·海亚姆、婆什迦罗第二、纳西尔·艾德丁·图西、Ghiyath al-Kashi（14世纪）、兀鲁伯（14世纪）、约翰·缪勒（1464）、瑞提克斯和瑞提克斯的学生Valentin Otho。

Madhava of Sangamagramma（约1400年）以无穷级数的方式做了三角函数的分析的早期研究。欧拉的《无穷微量解析入门》（Introductio in Analysin Infinitorum）（1748年）对建立三角函数在欧洲的分析处理做了最主要的贡献，他定义三角函数为无穷级数，并表述了欧拉公式，还有使用接近现代的简写 sin.、cos.、tang.、cot.、sec. 和 cosec.。

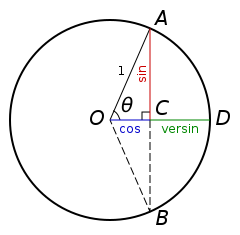
另一方面，所有基本三角函数都可依据中心为 O的单位圆来定义，类似于历史上使用的几何定义。特别是，对于这个圆的弦AB，这里的 θ 是对向角的一半，sin θ是 AC（半弦），这是印度的阿耶波多介入的定义。cosθ 是水平距离 OC，versin θ=1-cosθ是CD。tanθ是通过 A的切线的线段AE的长度，所以这个函数才叫正切。cotθ是另一个切线段 AF。 secθ=OE和 cscθ=OF是割线（与圆相交于两点）的线段，所以可以看作 OA沿着 A 的切线分别向水平和垂直轴的投影。DE是 exsecθ= secθ-1（正割在圆外的部分）。通过这些构造，容易看出正割和正切函数在 θ 接近 π/2的时候发散，而余割和余切在 θ 接近零的时候发散。

反三角函数

反三角函数并不能狭义的理解为三角函数的反函数，是个多值函数（就是说，你给一个值，有很多个角可以让其正弦等于这个值。这样的角有无数个。所以我们要规定其中一个，也就是落在[-π/2,π/2]范围上的这个角为我们要求的角）。

它是反正弦Arcsin x，反余弦Arccos x，反正切Arctan x，反余切Arccot x这些函数的统称，各自表示其正弦、余弦、正切、余切为x的角。

数学术语

为限制反三角函数为单值函数，将反正弦函数的值y限在-π/2≤y≤π/2，将y作为反正弦函数的主值，记为y=arcsin x；相应地，反余弦函数y=arccos x的主值限在0≤y≤π；反正切函数y=arctan x的主值限在-π/2<y<π/2；反余切函数y=arccot x的主值限在0<y<π。

　　反三角函数实际上并不能叫做函数，因为它并不满足一个自变量对应一个函数值的要求，其图像与其原函数关于函数y=x对称。其概念首先由欧拉提出，并且首先使用了【arc+函数名】的形式表示反三角函数，而不是f-1(x）。

　　⑴正弦函数y=sin x在[-π/2，π/2]上的反函数，叫做反正弦函数。arcsin x表示一个正弦值为x的角，该角的范围在[-π/2，π/2]区间内。【图中红线】

　　⑵余弦函数y=cos x在[0，π]上的反函数，叫做反余弦函数。arccos x表示一个余弦值为x的角，该角的范围在[0，π]区间内。【图中蓝线】

　　⑶正切函数y=tan x在(-π/2，π/2）上的反函数，叫做反正切函数。arctan x表示一个正切值为x的角，该角的范围在（-π/2，π/2）区间内。【图中绿线】

　　注释：【图的画法根据反函数的性质即：反函数图像关于y=x对称】

　　反三角函数主要是三个：

　　y=arcsin(x），定义域[-1，1] ，值域[-π/2，π/2]图象用红色线条；

　　y=arccos(x），定义域[-1，1] ，值域[0，π]，图象用蓝色线条；

　　y=arctan(x），定义域（-∞，+∞），值域（-π/2，π/2），图象用绿色线条；

　　y=arccot(x），定义域（-∞，+∞），值域（0，π），图象无；

　　sin(arcsin x)=x，定义域[-1，1]，值域 [-1，1] arcsin(-x)=-arcsinx

　　证明方法如下：设arcsin(x)=y，则sin(y)=x，将这两个式子代入上式即可得

　　其他几个用类似方法可得

　　cos(arccos x)=x，arccos(-x)=π-arccos x

　　tan(arctan x)=x，arctan(-x)=-arctanx

编辑本段 公式

　　反三角函数其他公式：

　　cos(arcsinx)=√(1-x^2)

　　arcsin(-x)=-arcsinx

　　arccos(-x)=π-arccosx

　　arctan(-x)=-arctanx

　　arccot(-x)=π-arccotx

　　arcsinx+arccosx=π/2=arctanx+arccotx

　　sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x

　　arcsin x = x + x^3/(2*3) + (1*3)x^5/(2*4*5) + 1*3*5(x^7)/(2*4*6*7）……+(2k+1)!!*x^(2k-1)/(2k!!*(2k+1))+……（|x|<1) !！表示双阶乘

　　arccos x = π -(x + x^3/(2*3) + (1*3)x^5/(2*4*5) + 1*3*5(x^7)/(2*4*6*7）……）（|x|<1)

　　arctan x = x - x^3/3 + x^5/5 -……

举例

　　当 x∈[-π/2，π/2] 有arcsin(sinx)=x

　　x∈[0，π]， arccos(cosx)=x

　　x∈（-π/2，π/2）， arctan(tanx)=x

　　x∈（0，π）， arccot(cotx)=x

　　x>0，arctanx=π/2-arctan1/x，arccotx类似

　　若 (arctanx+arctany）∈（-π/2，π/2），则 arctanx+arctany=arctan((x+y)/(1-xy))

　　例如，arcsinχ表示角α，满足α∈[-π/2，π/2]且sinα=χ;arccos(-4/5)表示角β，满足β∈[0，π]且cosβ=-4/5;arctan2表示角φ，满足φ∈（-π/2，π/2)且tanφ=2

编程应用

　　用三角函数算圆盘上的点，例如画钟表的刻度：CGPointMake(centerX + cos(angle) * radius , centerY + sin(angle) * radius); //angle为弧度

　　用反三角函数算圆盘旋转的弧度：CGFloat angleInRadians = atan2f(currentTouchPoint.y - center.y, currentTouchPoint.x - center.x) - atan2f(previousTouchPoint.y - center.y, previousTouchPoint.x - center.x);

posted on 2012-08-27 10:26 不及格的程序员-八神阅读(1502) 评论(0) 编辑收藏举报

刷新页面返回顶部