浅析基础数据结构-二叉堆
如题,二叉堆是一种基础数据结构
事实上支持的操作也是挺有限的(相对于其他数据结构而言),也就插入,查询,删除这一类
对了这篇文章中讲到的堆都是二叉堆,而不是斜堆,左偏树,斐波那契堆什么的 我都不会啊
更新概要:
无良博主终于想起来要更新辣
upd1:更新5.2.2-对于该子目所阐述的操作“用两个堆来维护一些查询第k小/大的操作”更新了一道例题-该操作对于中位数题目的求解
upd2:更新5.3-利用堆来维护可以“反悔的贪心”
continue...
一.堆的性质
1.堆是一颗完全二叉树
2.堆的顶端一定是“最大”,最小”的,但是要注意一个点,这里的大和小并不是传统意义下的大和小,它是相对于优先级而言的,当然你也可以把优先级定为传统意义下的大小,但一定要牢记这一点,初学者容易把堆的“大小”直接定义为传统意义下的大小,某些题就不是按数字的大小为优先级来进行堆的操作的
(但是为了讲解方便,下文直接把堆的优先级定为传统意义下的大小,所以上面跟没讲有什么区别?)
3.堆一般有两种样子,小根堆和大根堆,分别对应第二个性质中的“堆顶最大”“堆顶最小”,对于大根堆而言,任何一个非根节点,它的优先级都小于堆顶,对于小根堆而言,任何一个非根节点,它的优先级都大于堆顶(这里的根就是堆顶啦qwq)
来一张图了解一下堆(这里是小根堆)(原谅我丑陋无比的图)
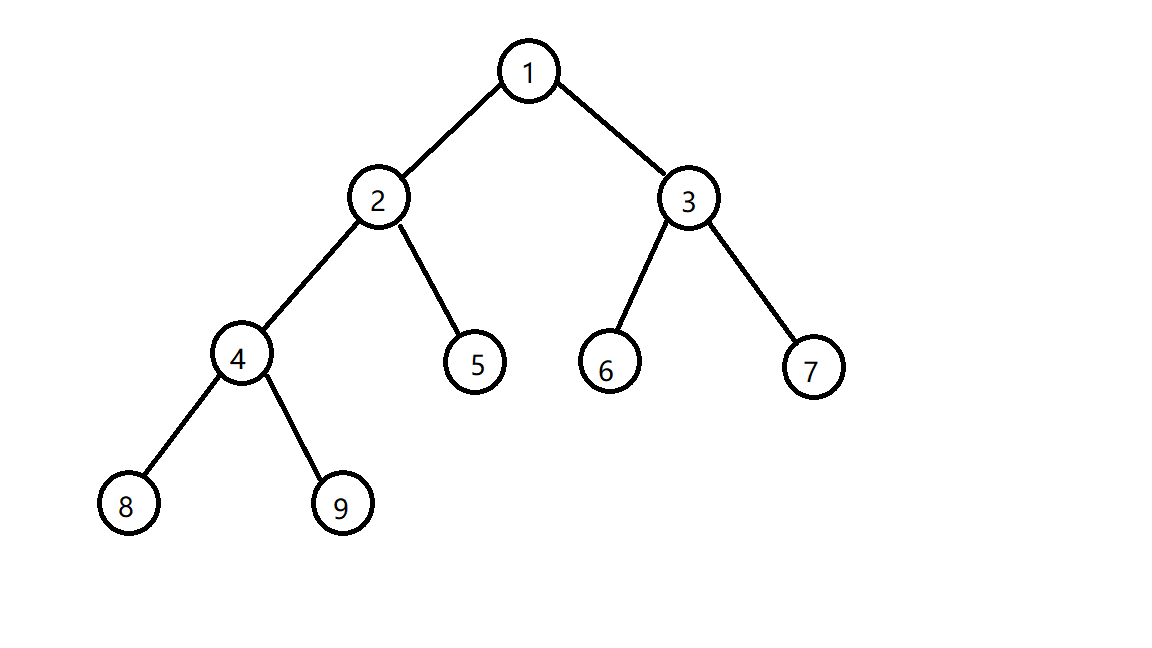
不难看出,对于堆的每个子树,它同样也是一个堆(因为是完全二叉树嘛)
二.堆的操作
1.插入
假设你已经有一个堆了,就是上面那个
这个时候你如果想要给它加入一个节点怎么办,比如说0?
先插到堆底(严格意义上来说其实0是在5的左儿子的,图没画好放不下去,不过也不影响)
然后你会发现它比它的父亲小啊,那怎么办?不符合小根堆的性质了啊,那就交换一下他们的位置
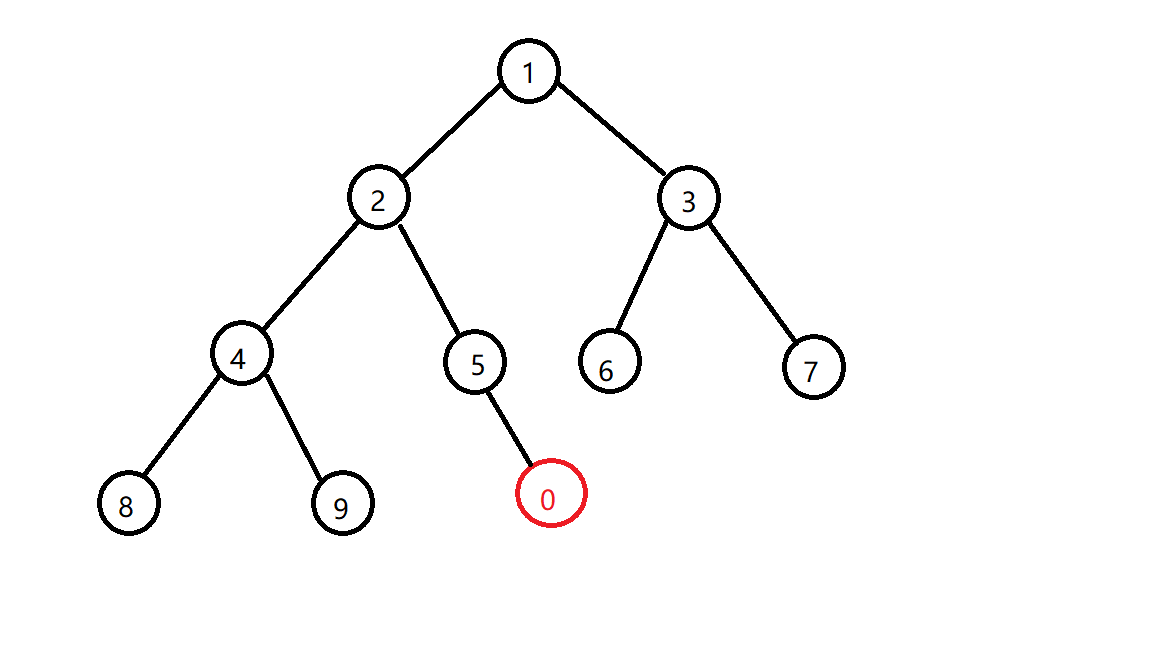
交换之后还是发现不符合小根堆的性质,那么再换
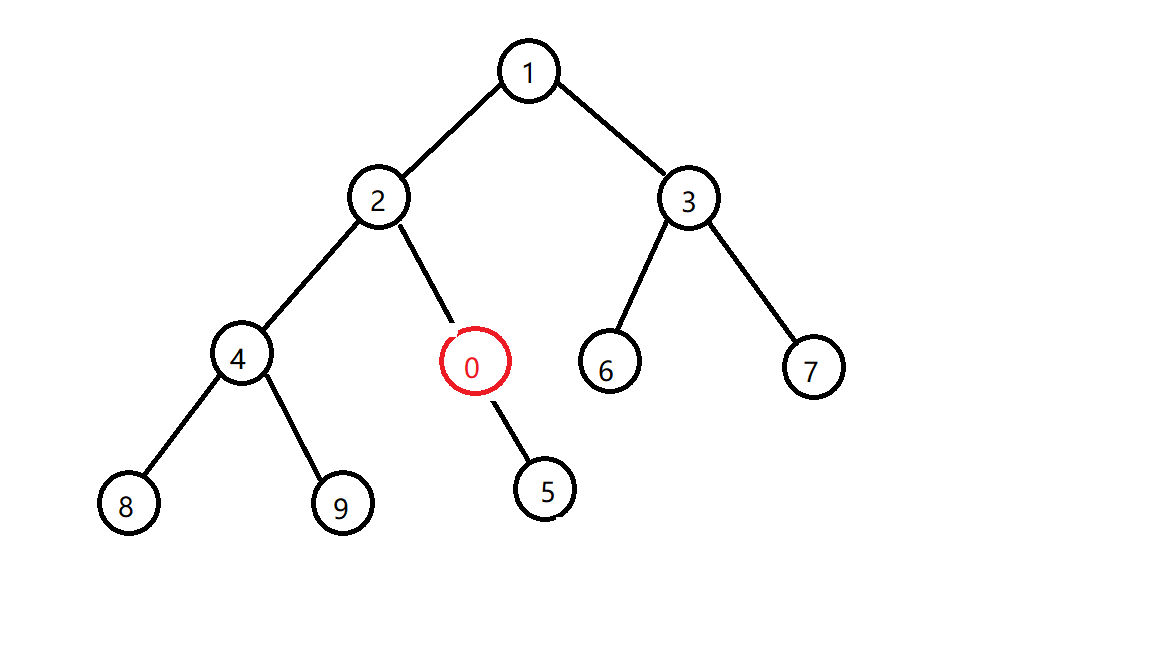
还是不行,再换
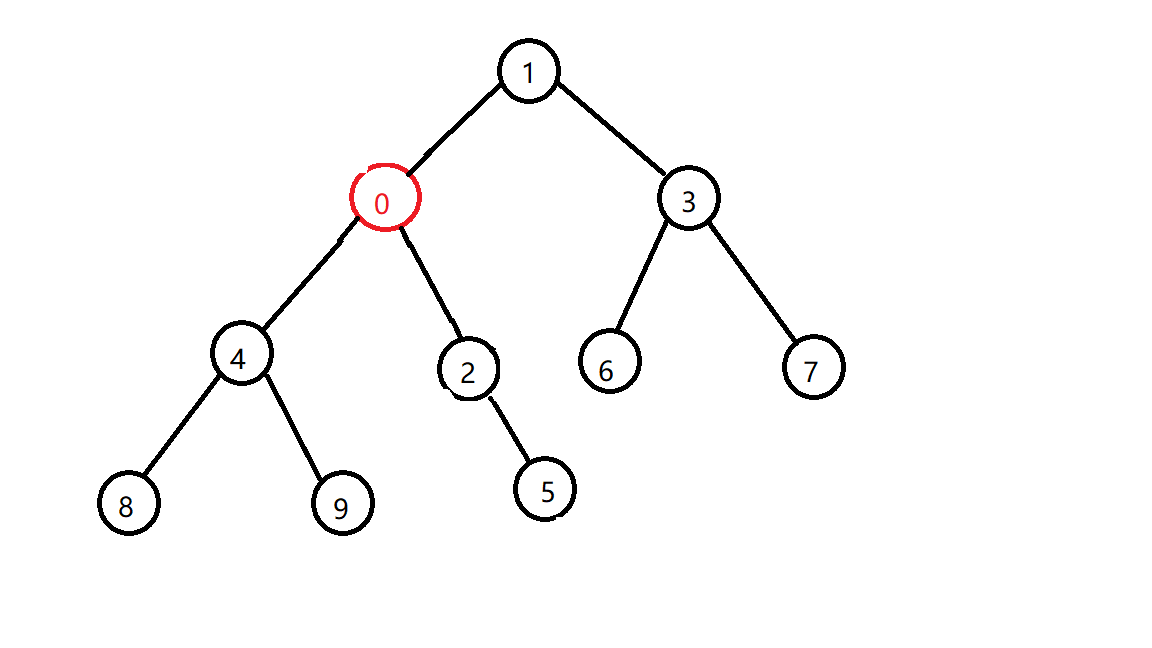
好了,这下就符合小根堆的性质了,是不是顺眼很多了?(假的,图越来越丑,原谅我不想再画)
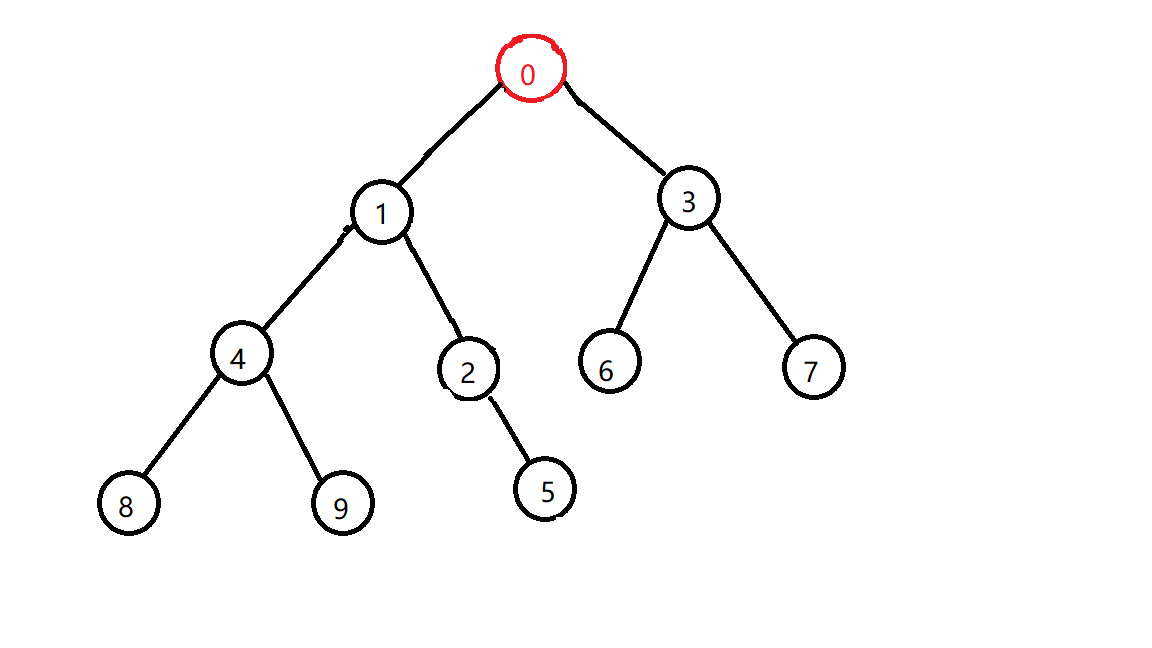
事实上堆的插入就是把新的元素放到堆底,然后检查它是否符合堆的性质,如果符合就丢在那里了,如果不符合,那就和它的父亲交换一下,一直交换交换交换,直到符合堆的性质,那么就插入完成了
Code:
void swap(int &x,int &y){int t=x;x=y;y=t;}//交换函数 int heap[N];//定义一个数组来存堆 int siz;//堆的大小 void push(int x){//要插入的数 heap[++siz]=x; now=siz; //插入到堆底 while(now){//还没到根节点,还能交换 ll nxt=now>>1;//找到它的父亲 if(heap[nxt]>heap[now])swap(heap[nxt],heap[now]);//父亲比它大,那就交换 else break;//如果比它父亲小,那就代表着插入完成了 now=nxt;//交换 } return; }
2.删除
把0插入完以后,忽然你看这个0不爽了,本来都是正整数,怎么就混进来你这个0?
于是这时候你就想把它删除掉
怎么删除?在删除的过程中还是要维护小根堆的性质
如果你直接删掉了,那就没有堆顶了,这个堆就直接乱了,所以我们要保证删除后这一整个堆还是个完好的小根堆

首先在它的两个儿子里面,找一个比较小的,和它交换一下,但是还是没法删除,因为下方还有节点,那就继续交换

还是不行,再换

再换

好了,这个碍眼的东西终于的下面终于没有节点了,这时候直接把它扔掉就好了

这样我们就完成了删除操作,但是在实际的代码操作中,并不是这样进行删除操作的,有一定的微调,代码中是直接把堆顶和堆底交换一下,然后把交换后的堆顶不断与它的子节点交换,直到这个堆重新符合堆性质(但是上面的方式好理解啊)
手写堆的删除支持任意一个节点的删除,不过STL只支持堆顶删除,STL的我们后面再讲
Code:
void pop(){ swap(heap[siz],heap[1]);siz--;//交换堆顶和堆底,然后直接弹掉堆底 int now=1; while((now<<1)<=siz){//对该节点进行向下交换的操作 int nxt=now<<1;//找出当前节点的左儿子 if(nxt+1<=siz&&heap[nxt+1]<heap[nxt])nxt++;//看看是要左儿子还是右儿子跟它换 if(heap[nxt]<heap[now])swap(heap[now],heap[nxt]);//如果不符合堆性质就换 else break;//否则就完成了 now=nxt;//往下一层继续向下交换 } }
3.查询
因为我们一直维护着这个堆使它满足堆性质,而堆最简单的查询就是查询优先级最低/最高的元素,对于我们维护的这个堆heap,它的优先级最低/最高的元素就是堆顶,所以查询之后输出heap[1]就好了
一般的题目里面查询操作是和删除操作捆绑的,查询完后顺便就删掉了,这个主要因题而异
三.堆的STL实现
这年头真的没几个人写手写堆(可能有情怀党?)
一是手写堆容易写错代码又多,二是STL 直接给我们提供了一个实现堆的简单方式:优先队列
手写堆和STL的优先队列有什么 区别?没有区别
速度方面,手写堆会偏快一点,但是如果开了O2优化优先队列可能会更快;
代码实现难度方面:优先队列完爆手写堆
这两方面综合起来,一般都是用STL的优先队列来实现堆,省选开O2啊
至于为什么前面讲堆的操作时用手写堆,好理解嘛,最好先根据上面的代码和图理解一下堆是怎么实现那些操作的,再来看一下下面的STL的操作
定义一个优先队列:
首先你需要一个头文件:#include<queue> priority_queue<int> q;//这是一个大根堆q priority_queue<int,vector<int>,greater<int> >q;//这是一个小根堆q //注意某些编译器在定义一个小根堆的时候greater<int>和后面的>要隔一个空格,不然会被编译器识别成位运算符号>>
优先队列的操作:
q.top()//取得堆顶元素,并不会弹出 q.pop()//弹出堆顶元素 q.push()//往堆里面插入一个元素 q.empty()//查询堆是否为空,为空则返回1否则返回0 q.size()//查询堆内元素数量
常用也就这些,貌似还有其他,不过基本也用不到,知道上面那几个也就可以了
不过有个小问题就是STL只支持删除堆顶,而不支持删除其他元素
但是问题不大,开一个数组del,在要删除其他元素的时候直接就标记一下del[i]=1,这里的下标是元素的值,然后在查询的时候碰到这个元素被标记了直接弹出然后继续查询就可以了 (前两天刚从学长处get这个姿势)
另外因为STL好写,下面堆的应用全部都会采用STL的代码实现(懒啊,如果有放代码的话)
这里补一下重载运算符在STL的优先队列中应用到的知识
重载运算符是什么?
把一种运算符变成另外一种运算符(注意,都必须是原有的运算符),比如把<号重载成>号,这个东西学过STL中的sort的同学应该会比较熟悉
这个在优先队列中有什么用处呢?
之前我们就讲到了,大根堆,小根堆的“大”和“小”都不是传统意义下的“大”和“小”,重载运算符在STL的优先队列中就是用来解决这种“非传统意义的‘大’和‘小’”的
现在你有一个数列,它有权值和优先级两种属性,权值即该数的大小,优先级是给定的,现在要你按照优先级的大小从小到大输出这个数列
这不是Treap吗?这不是sort吗?
以上两个东西都可以用来实现这道题(逃,而且就实用性而言,sort用来解决这道题是最方便的,但是我们现在要讲的做法是使用堆排序的方式来解决这道题(堆排序是什么?下文堆的应用中有提到)
首先应该想得到结构体,我们定义一个结构体
struct node{ int val,rnd; }int a[100];
但是使用传统做法是行不通的,在小根堆中是通过比较数的大小来确定各个元素在堆中的位置的,但是对于这个a数组,你是要对比权值val的值,还是要对比优先级rnd的值?
这时候重载运算符就派上用场了
我们在结构体里面再加3行东西
struct node{ int val,rnd; bool operator < (const node&x) const { return rnd<x.rnd; } }a[100];
这个玩意为什么要这么写呢?
首先这个玩意是bool类型的,因为你只需要判断这两个是大,还是小;然后,要重载运算符就必须加一个operator这个玩意,不然计算机怎么知道你要干嘛?后面接一个你要重载的运算符,这里是“<”,再后面的括号里面的东西则是你要比较的数据类型,这里是数据类型为node,并且加了一个指针&,将对这个x的修改同步到你实际上要修改的数据那里。然后就是记得加那两个const
然后两个大括号里面就是你重载的内容了,这里是把比较数的大小的小于号,重载成比较node这个数据类型里面的优先级的大小
这个玩意讲的比较多,主要是因为是一个很难懂的东西(对我来说?反正当时学的时候就是感觉很晦涩难懂,这里就尽量写详细一点,给和当初的我一样的萌新看一下)
而且在实际中,这个东西的用处也很大,就说在堆里面的应用,在NOIP提高,省选的那个级别,就绝对不可能考裸的堆的,往往你要比较的东西就不是数的大小了,而是按照题目要求灵活更改,这时候重载运算符就帮得上很大忙了
这也就是为什么我在前面反复强调,堆里面的大小,并非传统意义下的大小
四.堆的复杂度
因为堆是一棵完全二叉树,所以对于一个节点数为n的堆,它的高度不会超过log2n
所以对于插入,删除操作复杂度为O(log2n)
查询堆顶操作的复杂度为O(1)
五.堆的应用
1.堆排序
其实就是用要排序的元素建一个堆(视情况而定是大根堆还是小根堆),然后依次弹出堆顶元素,最后得到的就是排序后的结果了
但是裸的并没有什么用,我们有sort而且sort还比堆排快,所以堆排一般都没有这种模板题,一般是利用堆排的思想,然后来搞一些奇奇怪怪的操作,第2个应用就有涉及到一点堆排的思想
2.用两个堆来维护一些查询第k小/大的操作
利用一个大根堆一个小根堆来维护第k小,并没有强制在线
不强制在线,所以我们直接读入所有元素,枚举询问,因为要询问第k小,所以把前面的第k个元素都放进大根堆里面,然后如果元素数量大于k,就把堆顶弹掉放到小根堆里面,使大根堆的元素严格等于k,这样这次询问的结果就是小根堆的堆顶了(前面k-1小的元素都在大根堆里面了)
记得在完成这次询问后重新把小根堆的堆顶放到大根堆里面就好

#include <cstdio> #include <vector> #include <cstring> #include <queue> #define ll long long #define inf 1<<30 #define il inline #define in1(a) read(a) #define in2(a,b) in1(a),in1(b) #define in3(a,b,c) in2(a,b),in1(c) #define in4(a,b,c,d) in2(a,b),in2(c,d) il int max(int x,int y){return x>y?x:y;} il int min(int x,int y){return x<y?x:y;} il int abs(int x){return x>0?x:-x;} il void swap(int &x,int &y){int t=x;x=y;y=t;} il void readl(ll &x){ x=0;ll f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} x*=f; } il void read(int &x){ x=0;int f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} x*=f; } using namespace std; /*===================Header Template=====================*/ #define N 200010 priority_queue<int,vector<int>,greater<int> > q; priority_queue<int> q1; int n,m,a[N],b[N]; int main(){ in2(n,m); for(int i=1;i<=n;i++)in1(a[i]); for(int i=1;i<=m;i++)in1(b[i]); int i=1; for(int j=1;j<=m;j++){ for(;i<=b[j];i++){ q1.push(a[i]); if(q1.size()==j)q.push(q1.top()),q1.pop(); } printf("%d\n",q.top()); q1.push(q.top());q.pop(); } return 0; }
中位数
中位数也是这种操作可以解决的一种经典问题,但是实际应用不大(这种操作的复杂度为$O(nlogn)$,然而求解中位数有$O(n)$做法)
Luogu中也有此类例题,题解内也讲的比较清楚了,此处不再赘述,读者可当做拓展练习进行食用
提示:设序列长度为$N$,则中位数其实等价于序列中$N/2$大的元素
事实上堆在难度较高的题目方面更多的用于维护一些贪心操作,以降低复杂度,很少会有题目是以堆为正解来出的了,更多的,堆在这些题目中处于“工具”的位置
3.利用堆来维护可以“反悔的贪心”
题目:Luogu P2949 [USACO09OPEN]工作调度Work Scheduling
这道题的话算是这种类型应用的经典题了
首先只要有贪心基础就不难想出一个解题思路:因为所有工作的花费时间都一样,我们只要尽量的选获得利润高的工作,以及对于每个所选的工作,我们尽量让它在更靠近它的结束时间的地方再来工作
但是两种条件我们并不好维护,这种两个限制条件的题目也是有一种挺经典的做法的:对一个限制条件进行排序,对于另一个限制条件使用某些数据结构来维护(如treap,线段树,树状数组之类),但是这并不在我们今天的讨论范畴QAQ
考虑怎么将这两个条件“有机统一”。
排序的思路是没有问题的,我们可以对每个工作按照它的结束时间进行排序,从而来维护我们的第二个贪心的想法。
那么对于这样做所带来的一个冲突:对于一个截止时间在d的工作,我们有可能把0~d秒全都安排满了(可能会有多个任务的截止时间相同)
怎么解决这种冲突并保证答案的最有性呢?
一个直观的想法就是把我们目前已选的工作全部都比较一下,然后选出一个创造的利润最低的工作(假设当前正在决策的这个工作价值很高),然后舍弃掉利润最低的工作,把这个工作放进去原来的那个位置。(因为我们已经按照结束时间排序了,所以舍弃的那个任务的截止完成时间一定在当前决策的工作的之前)
但是对于大小高达$10^6$的n,$O(n^2)$的复杂度显然是无法接受的,结合上面的内容,读者们应该也不难想出,可以使用堆来优化这个操作
我们可以在选用了这个工作之后,将当前工作放入小根堆中,如果堆内元素大于等于当前工作的截止时间了(因为这道题中,一个工作的执行时间是一个单位时间),我们就可以把当前工作跟堆顶工作的价值比较,如果当前工作的价值较大,就可以将堆顶弹出,然后将新的工作放入堆中,给答案加上当前工作减去堆顶元素的价值(因为堆顶元素在放入堆中的时候价值已经累加进入答案了)。如果堆内元素小于截止时间那么直接放入堆中就好
至此,我们已经可以以$O(nlogn)$的效率通过本题
而通过这道题我们也可以发现,只有在优化我们思考出来的贪心操作的时间复杂度时,我们才用到了堆。正如我们先前所说到的,在大部分有一定难度的题目里,堆都是以一个“工具”的身份出现,用于优化算法(大多时候是贪心)的时间复杂度等

#include <cstdio> #include <algorithm> #include <queue> #include <vector> #include <map> #include <set> using namespace std ; #define N 100010 #define int long long int n , m ; struct node { int d,p ; bool operator < ( const node &x ) const { return p>x.p; } } a[ N ] ; bool cmp( node a , node b ) { return a.d==b.d?a.p<b.p:a.d<b.d; } priority_queue< node > q ; signed main() { scanf( "%lld" , &n ) ; for( int i = 1 ; i <= n ; i ++ ) { scanf( "%lld%lld" , &a[i].d , &a[i].p ) ; } sort(a+1,a+n+1,cmp); int ans = 0 ; for( int i = 1 ; i <= n ; i ++ ) { if( a[i].d<=(int)q.size() ) { if( q.top().p<a[i].p ) { ans += a[i].p-q.top().p ; q.pop() ; q.push(a[i]) ; } } else q.push(a[i]) , ans += a[ i ].p ; } printf( "%lld\n" , ans ) ; }
continue...



