在围观中学习

多动动脑子吧

已经完成了：

16/156

agc001_d

Problem：

从前有$a$、$b$两个序列，一个长度为$n$的字符串，其中

1）前$a_1$个是回文串，接下来$a_2$个是回文串，接下来$a_3$个是回文串，以此类推

2）前$b_1$个是回文串，接下来$b_2$个是回文串，接下来$b_3$个是回文串，以此类推

由前两个可以推得：

3）$n$个字符全部相等

现在丢失了这两个序列，只知道给出的$A$是$a$的一个排列，问你序列$a$、$b$

Solution：

就是按回文串的方式相等的连边，然后使得$n$个联通

首先如果$A$中有大于两个奇数时是肯定无解的

然后把两个奇数放在两边，输出$a_1-1,a_2,a_3,\cdots,a_m+1$就行了

$n=1$要特判

agc001_e

Problem：给出$n$对数$(a_i,b_i)$，求

$$ans=\sum_{1\leq i<j\leq n}\dfrac{(a_i+a_j+b_i+b_j)!}{(a_i+a_j)!(b_i+b_j)}$$

Solution：

解法很妙

把问题转化成从$(-a_i,-b_i)$到$(a_j,b_j)$的路径条数

那就是很简单的dp了

然后再减去$i$自己重复的再除以$2$就行了

agc002_d

Problem：给出$n$个点$m$条边，第$i$条边边权为$i$，每次询问给出$x$、$y$、$z$，求$x$和$y$构成总大小为$z$的联通块用到最大的边权最小是多少

Solution：显然整体二分+可持久化并查集

不会可持久化怎么办

只要在合并的时候启发式合并，不进行路径压缩，并查集就可撤销了
agc002_e

Problem：有$n$堆石子，两人分别操作，要不就每一堆各拿一个，要不就把最大的那堆拿走，谁吃最后一个输

Solution：转化成平面图，发现对角线必胜必败相同

agc002_f

Problem：$n$种颜色的棋子，每种各有$K$个，排列出来把最左边的染成$0$，问最终序列方案数

Solution：先不考虑每种颜色的顺序，然后就能转化成求拓扑序的方案数

$f_{i,j}$表示上面$i$个下面$j$列的方案数

就是这样

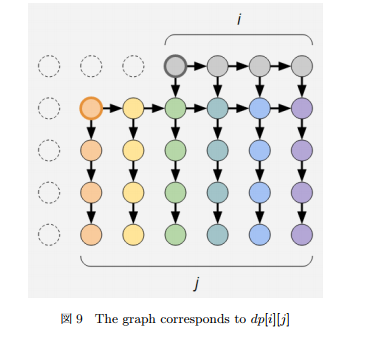
然后就很好做了

agc003_d

Problem：给你$n$个数，要求你找一个最大的集合使得不存在有两个数相乘是一个立方数

Solution：计算$Norm_i$和$Pair_i$，分别表示需要乘上最小的数和除以最小的数使得它变成一个立方数

那么对于$Norm_i$相同的数$Pair_i$肯定相同，如果$Norm_i=Pair_j$，那么这两个数就会存在矛盾

可以证明一类数只会与唯一一对数产生矛盾

这时候就取这两类数多的那一类加入集合即可（如果存在$Norm_i=Pair_i=1$的数，只能加入其中的一个数）

问题就转化成求$Norm_i$和$Pair_i$

筛出$(10^{10})^{\frac{1}{3}}$以内的质数并质因数分解，这里面的质数可以直接处理

假如剩下的数为$s$

1）这是一个质数$p$

2）这是一个质数的平方$p^2$

3）这是两个质数的乘积$pq$

那么对于1、3两种情况$Norm_i=s^2$，而第2种情况$Norm_i=\sqrt(s)$

这是很好判断的

agc003_e

Problem：给出一开始$1,2,3,\cdots,n$的数列，给出$Q$个操作

每次操作把原串循环拓展到无限，然后取前$q_i$个作为现在的串，问你最终的串每种数字分别有多少个

Solution：在头加入一个$q_0=n$更方便

如果$q_i\geq q_{i+1}$，那么$q_i$就没啥用了

就用单调栈搞出有用的单调递增的序列

记录$t_i$表示在$i$操作后的串在最终的串中出现了多少次，$t_m=1$

$i$从大到小处理

定义还未处理的后缀长度$k$，初始$k=q_i$，然后循环以下过程

找最大的$q_j<=k$

$t_j$加上$\lfloor\dfrac{k}{q_j}\rfloor t_i$

$k$再模$q_j$

最后剩下的$k$就表示做完$i$操作之后后缀长度为$k$的是数列$1,2,3,\cdots,k$

然后处理以下就行了

agc003_f

Problem：给你一个$H\times W$的矩阵，其中#表示黑点且保证联通，问你把它扩大$K$次之后有多少个联通块

Solution：如果存在一行第一个和最后一个都是黑点并且存在一列第一个和最后一个都是黑点，那么最后都会联通，输出$1$即可

如果两种都不存在，最后的就是$sum\_black\_cell^{K-1}$个联通块

否则就矩阵乘法一下.. 至于怎样就自己推吧

agc004_c

Problem：给出一个矩阵，要求你求出两个矩阵，使得这两个矩阵的交恰好是给出的矩阵且两个矩阵中的黑点都联通

题目保证给出的矩阵最外一圈没有点

Solution：先这样铺

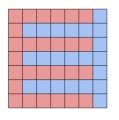
然后哪里有黑点就搞一下就好了

agc004_d

Problem：给出$n$个点，每个点都有下一个节点$nxt_i$，现在要求你去更改这些点，使得所有点沿着下一个节点走$K$次都恰好到$1$

Solution：首先$1$一定要指向$1$，然后就树形dp，长度一超过$K$就连到$1$去

agc004_e

Problem：一个矩阵上有很多机器人，你可以同时对他们下命令四个方向，走出边界就爆炸，问你最多有多少个可以存活

Solution：相当于让拯救点走，那么爆炸的机器人范围就与上下左右走过最远的点有关

然后就可以dp了

agc004_f

Problem：给出一棵树或者环套树，每次可以翻相邻两个相同颜色点的颜色，问你最少要翻多少次使得全白变全黑

Solution：对原图的生成树黑白染色，每次翻相邻两个点就相当于移动一个黑点

1）树

只需要判断黑点个数是否等于白点个数即可

然后统计每条边的贡献即可

2）环套树，且环使奇环

对于这一条返祖边，如果操作就是把两个白变黑或者把两个黑变白

就相当于加上两个黑点或者减去两个黑点

判断原图黑点与白点奇偶是否相同即可

在一个点囤积若干个黑点对答案是没有影响的

所以就先在返祖边连接的两个点囤积所需的黑点再像树一样做即可

3）环套树，且环为偶环

判断黑点个数是否等于白点个数，因为这条返祖边无法增加或减少黑点个数

假设要在这条边上运送$x$个黑点，那么每条边运送量都是关于$x$的一次函数

那么就是数轴上的中位数了

agc005_c

Problem：有一棵$n$个点的树，每个点离最远的点的距离为$a_i$，问你存不存在这样的树

Solution：找到直径后就很好判断了

agc005_d

Problem：求$n$个点排列的方案数，使得$|p_i-i|\not=K$

Solution：容斥，求至少有$i$条不合法边的方案数，发现互相影响的边是连起来的链，就很好dp了
agc005_e

Problem：A有一棵蓝色边的树，B有一棵红色边的树，每人每回合可以移动到相邻节点或者不动，现在B要追A，问是否追的上，要多少个回合

Solution：建出以B起始点的树

对于A树上的边，如果在B树上距离大于$2$，就是说A到了这个节点之后只要B不在旁边就再也追不上了

除去这些边，剩下的就只有距离为$1$和$2$的了，有一个结论是这些边不能使A走出B的子树

那么就看哪些节点是A先到达的，如果之中存在那些追不上的节点就输出$-1$，否则就只能停在最远的那个节点等死
agc005_f

Problem：$n$个点的树，求$f(K)$

$f(K)$表示在树上任意取$K$个节点用最小的联通块覆盖它的块大小总和

Solution：对于一个任意给定的$K$，考虑任意一条边，用上了这条边且覆盖了$K$个点的方案数为$C_n^K-C_A^K-C_{n-A}^K$，其中$A$是其子树大小

那么所有边的总和再加上$C_n^K$就是答案，这样我们就得到了$O(n)$的解决方法

设能把树分成一块大小为$i$的有$b_i$种，那么$

$$ff(K)=nC_n^K-\sum b_iC_i^K$$

把组合数拆开

$$f(K)=nC_n^K-\sum b_i\dfrac{i!}{K!(i-K)!}$$

$$f(K)=nC_n^K-\dfrac{1}{K!}\sum (b_i i!)\dfrac{1}{(i-K)!}$$

然后就可以NTT做了，原根是$5$

agc006_c
agc006_d
agc006_e
agc006_f
agc007_c
agc007_e
agc007_f
agc008_d
agc008_e
agc008_f
agc009_b
agc009_c
agc009_d
agc009_e
agc010_c
agc010_d
agc010_e
agc010_f
agc011_c
agc011_d
agc011_e
agc011_f
agc012_c
agc012_d
agc012_e
agc013_c
agc013_d
agc013_e
agc014_d
agc014_e
agc015_c
agc015_d
agc015_e
agc015_f
agc016_b
agc016_c
agc016_d
agc016_e
agc016_f
agc017_d
agc017_e
agc017_f
agc018_b
agc018_c
agc018_d
agc018_e
agc018_f
agc019_c
agc019_d
agc019_e
agc019_f
arc058_d
arc062_e
arc062_f
arc063_e
arc063_f
arc064_f
arc065_e
arc065_f
arc066_e
arc066_f
arc067_f
arc068_e
arc068_f
arc069_f
arc070_f
arc071_f
arc072_e
arc072_f
arc073_e
arc073_f
arc074_e
arc074_f
arc075_f
arc076_e
arc076_f
arc077_e
arc077_f
arc078_e
arc078_f
arc079_f
arc080_e
arc080_f
arc081_f
arc082_e
arc082_f
arc083_e
arc083_f