单变量微积分笔记30——无穷级数和收敛判定
希腊的哲学家芝诺曾经辩论说,一支箭永远不能达到它的目标。他说,首先箭要到达目标距离的一半,然后又必须到达剩余距离的一半,然后还有一半,这样就没有穷尽。因为这个旅程有无限个部分,所以箭要花费无限的时间才能结束这个旅程。这就是“芝诺悖论”。芝诺的结论是——时间是不存在的。尽管他自己也不相信这个结论。这个问题看似诡异,但在数学面前,神秘荡然无存,破解问题的关键就是无穷级数。
悖论的谜底
把芝诺问题用数学表达就是:

更普遍的写法是:

其实很早就有人揭开了悖论的谜底,先将等号两边同时乘以a:
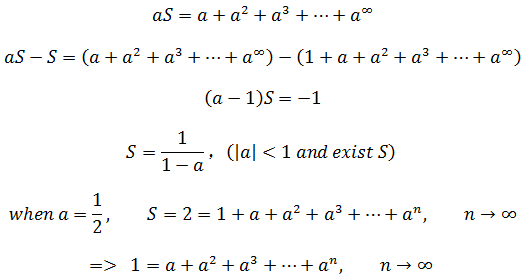
所以芝诺问题的最终答案是1。需要注意的是,只有当 -1 < a < 1时上述公式才成立,否则结果将是发散的。
无穷级数
对于和几何级数类似的和式,用数学符号表示:
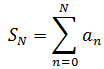
称SN为部分和,当N→∞时,和式就是无穷极限:
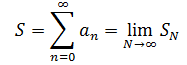
无穷极限S的结果可能是收敛的,有可能是发散的。
无穷级数的收敛性
我们感兴趣的第一个问题是无穷级数的收敛性。
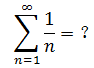
上式的收敛性没有那么明显,应当如何判断?
仔细观察上式会发现,它和黎曼和及其类似,如果Δx =1,那么
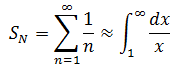
需要注意的的,二者接近但并不相等,积分处理的是当Δx→0的情况。
对于黎曼和,如果当Δx = 1时使用左矩形公式(数值积分可参考《数学笔记19——数值积分》),则:
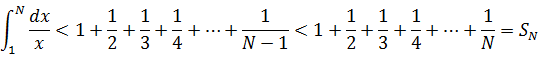
如果使用右矩形公式,则:
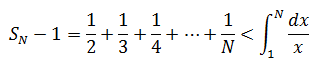
综上:
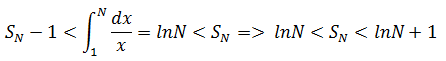
由于lnN是发散的,所以SN也是发散的。
积分比较判别法
上面的例子展示了和式和积分的关系,这样描述“积分比较法”:如果f(x)是减函数,且f(x) > 0,则:
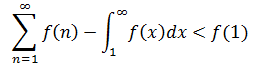
和式和积分的收敛性一致。
积分比较的基本思想就是用积分代替和式,因为和式通常很难计算,但和式对应的积分往往很容易,所以需要化繁为简,这也是数学的基本思想。
极限比较判别法
与积分比较类似,如果f(x)等价于g(x),即x→∞时f(x)/g(x) = 1,其中n > 0, f, g >,则∑f(x)和∑g(x)的收敛性一致。
比值判别法
当积分法和极限法出现困难时,比值法将是一个值得尝试的方案,对于∑an,an > 0 来说,

如果L < 1,∑an是收敛的;如果L > 1∑an是发散的;如果L = 1,不能使用比值判别法。
示例
判断下面三个式子的收敛性:
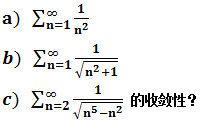
a.使用积分判别法
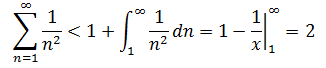
答案是收敛的,最终结果≈2
该求解过程也可以推广到f(x) = 1/nm
b.使用极限比较判别法
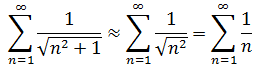
结果是发散的。
c.使用极限比较判别法
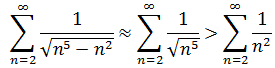
结果是收敛的。
综合示例
示例1
判断下面三个式子的收敛性:
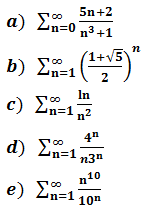
a.使用极限比较判别法
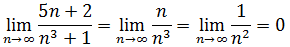
答案是收敛。
b.
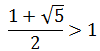
题目是几何级数,答案是发散。
c.使用极限比较判别法
lnn << n,lnn/n2 << 1/n,所以结果是收敛。
d.使用比值判别法
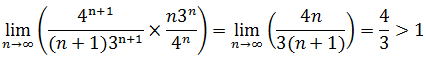
答案是发散。
e.使用比值判别法
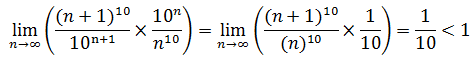
答案是收敛的。
示例2
判断下面式子的收敛性:
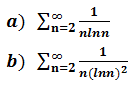
a.使用积分判别法,
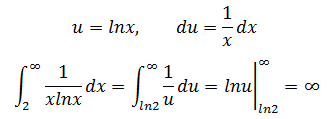
答案是发散
b.使用积分判别法,
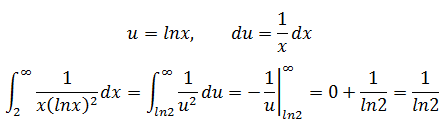
答案是收敛的。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




