深入理解拉格朗日乘子法

一个最短路径问题

假设你在M点，需要先到河边再回到C点，如何规划路线最短？

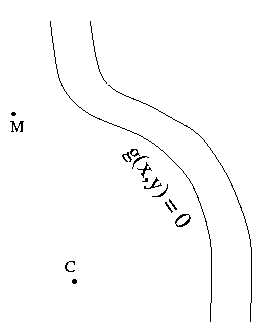
假设：
河流曲线满足方程 \(g(x,y) = 0\)（例如 如果它是一个圆：\(g(x,y)=x^2+y^2-r^2=0\)），用P表示河边上的任意 \(P(x,y)\) 点，用 \(d(M,P)\) 表示M,P之间距离，那么问题可以描述为：$max f(P) $, 约束于 \(g(P)=0\)。\(g(x,y)=x^2+y^2-r^2=0\)

如何求解问题？

1. 从几何意义中获得灵感：

首先，\(f(P)\) 是一个标量（只有大小没有方向），那么在上图的二维空间中必然存在了一个标量场 \(f(P)\)，即对于每一个点P都对应着一个 \(f(P)\)值，它代表经过该点的路径总和是多少。
如果我们画出它的等值线（场线)，就会发现它呈椭圆向外辐射：

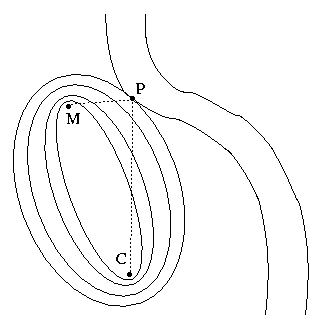
显然，\(f(P)\)的等值线与河边曲线的交点P即为我们想求的点。

那么问题来了: 这样的点满足何种性质？（如果没有性质也就无法列出关系式进行求解，但是这么特殊的点极有可能存在良好某种特性）

最直观的性质： 等值线（椭圆）在P点的法向量n与河边曲线的法向量m平行：

\(n= \lambda m\)

而在多元微积分中，一个函数h在某一点P的梯度是点P所在等值线（二维）或等值面（三维）的法向量，即\(n= \nabla h(P)\) ,所以对于函数 f , g ：

\(n = \lambda m \Rightarrow \nabla f(P) = \lambda \, \nabla g(P) \Rightarrow \begin{pmatrix} f_{x}\\ f_{y} \end{pmatrix} = \lambda\begin{pmatrix} g_{x}\\ g_{y} \end{pmatrix} \Rightarrow f_{x} = \lambda g_{x} \; (1) \\ f_{y} = \lambda g_{y} \; (2)\)

即由相交点的性质我们得到了2个关系式（因为是二维平面，对于三维则可以得到三个关系式，以此类推），

再加上我们的约束条件：

\(g(P)=g(x,y)=0 \; (3)\)

一共三个关系式。由线性代数中知识可知3个关系式，3个未知量，\((x,y,\lambda)\) 极可能有唯一解，当然也不排除会出现多个解甚至无穷多解 （例如下图河边是一条直线，且M,C就在河边时）。

2. 从数学公式中获得灵感

仍然是问题：

\(max f(P) = d(M,P) + d(P, C)\)
\(subject to: g(P) = 0\)

我们知道在多元微积分中如果想求一个函数的极值一般的做法是把 \(\nabla f(P)=0\) ，如何把这个公式和我们的约束条件 \(g(P)=0\) 统一在一起呢？

答案是引入\(\lambda\) 并且定义一个新的函数 \(F(P,\lambda)=f(P)- \lambda g(P)\) ,

令： \(\nabla F(P, \lambda) = \nabla F(x,y, \lambda)= \begin{pmatrix}F_{x} \\F_{y} \\F_{\lambda}\end{pmatrix}=0\) 与我们要求解的优化问题是等价的。

\(F_{x} = 0 \Rightarrow f_{x} - \lambda g_{x} = 0 \Rightarrow f_{x} = \lambda g_{x} \; (1) \\F_{y} = 0 \Rightarrow f_{y} - \lambda g_{y} = 0 \Rightarrow f_{y} = \lambda g_{y} \; (2)\\g(x,y) = 0 \; (3)\)