梯度下降
梯度下降是优化中常用的一种寻优策略,很自然的被引入NN中。本文只对NN中的梯度下降进行介绍。梯度下降算法的核心就是不断计算当前损失函数的梯度,在NN中为了更好的计算梯度,引出了后向传播算法,其实就是为了计算梯度而已。
Ok,假设我们已经有了一个比较复杂的网络,其中参数theta是我们想要求出来的值。
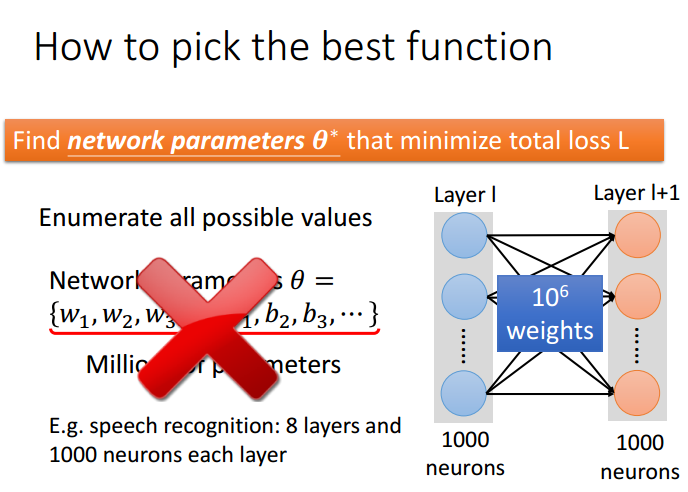
寻找最好的函数,就是为神经网络选取一组最好的系数theta使得损失函数最小。但,显然我们不能通过遍历的方式进行寻找系数。例如含有1000个neuron的两层神经网络结构中,第一层的输出为1000个值,对应第二层的每个neuron就有1000个weights,所以需要的参数就是1000*1000+1000(偏置)。
梯度下降算法是最优化求解中常用的经典算法,把损失函数作为所求参数的函数。然后通过利用函数的梯度和学习步长,不断迭代寻找最优参数,优点是适用面广,速度快,缺点是只能获得局部最优
例如,损失函数为L,参数集合为theta,是关于omega的函数。


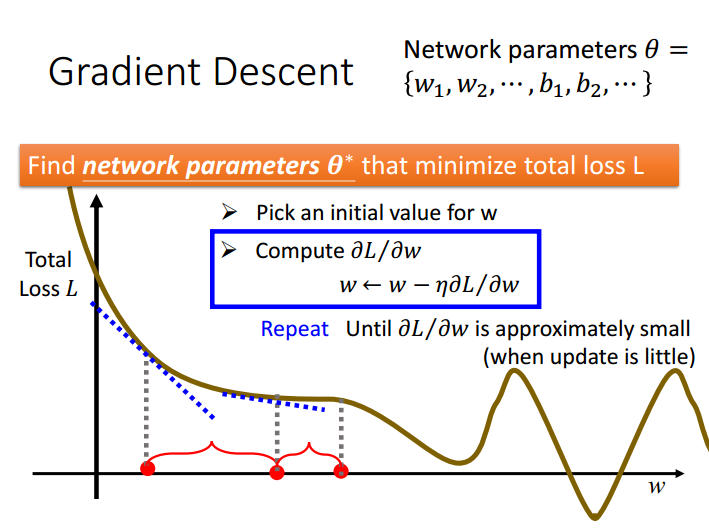
每次沿着负梯度方向移动:

通过不断迭代,最终得到一个局部最优解。下面为一个例子:


总结:
梯度下降十分经典,相关资料很多,这里不进行复述。这里主要讲讲梯度下降训练神经网络和神经网络中前向,后向传播算法的关系。
首先,整个函数的损失函数为L,对损失函数进行求导,得到theta的初始导数,然后根据学习步长与导数不断更新。

为了更新,我们需要求得损失函数的导数,需要用到链式法则,具体如下:

损失函数是所有损失的累加。但是损失函数对系数omega的导数不能直接求出,需要传递:
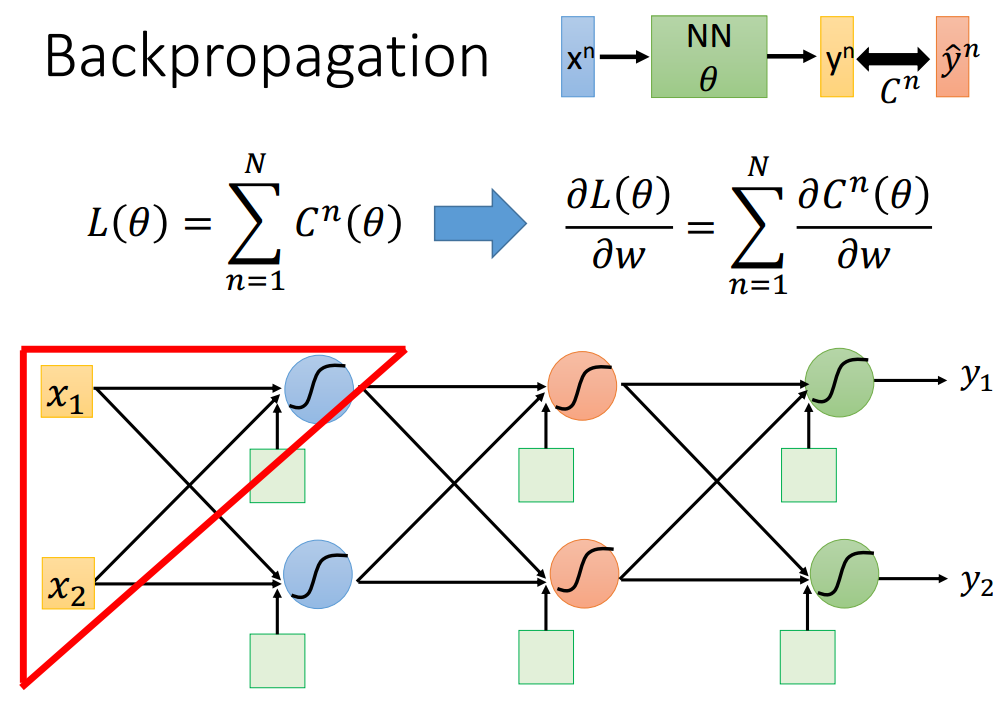
例如,求上图中红色三角区域内参数(w1和w2),通过链式法则我们可以得到该梯度由两部分组成,具体如下:

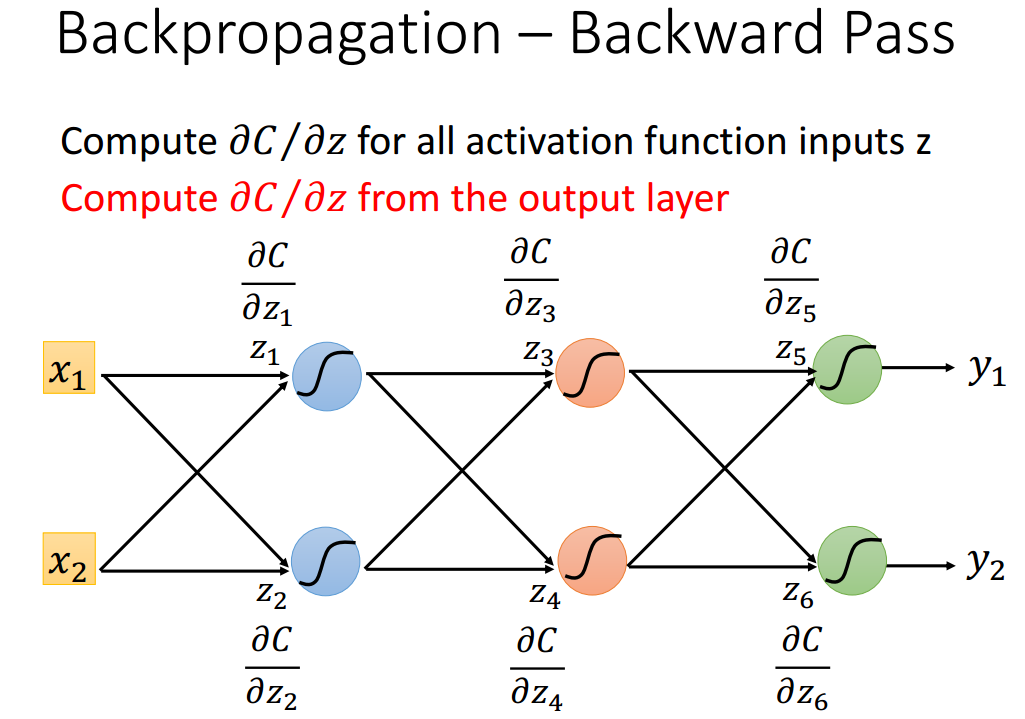
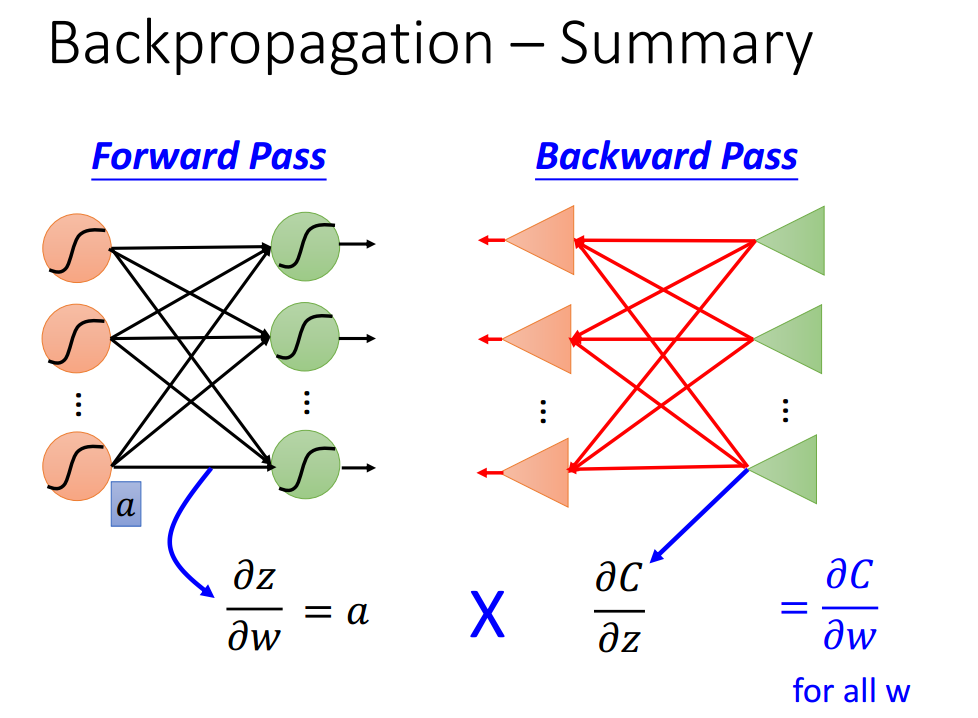
所有参数的导数(z对w的导数),这部分由前向传播决定;激活函数输入的梯度(c对z的导数),这部分由后向传播决定,所以需要配合使用。其中还有其他层的梯度信息,暂时用问号代替。
惊喜的发现,所有参数的梯度竟然就是与权值相连的输入值。问号是指网络中所有与权值相连的如输入值,Amazing!

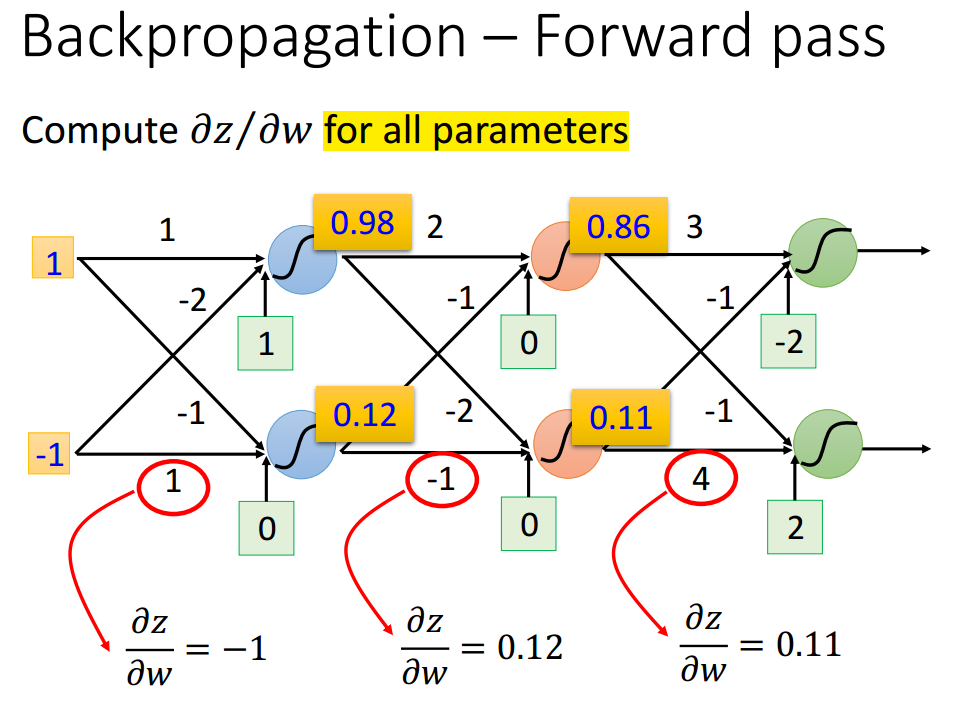
所以,我们得到了全部参数的导数之后,就开始计算激活函数输入的导数:
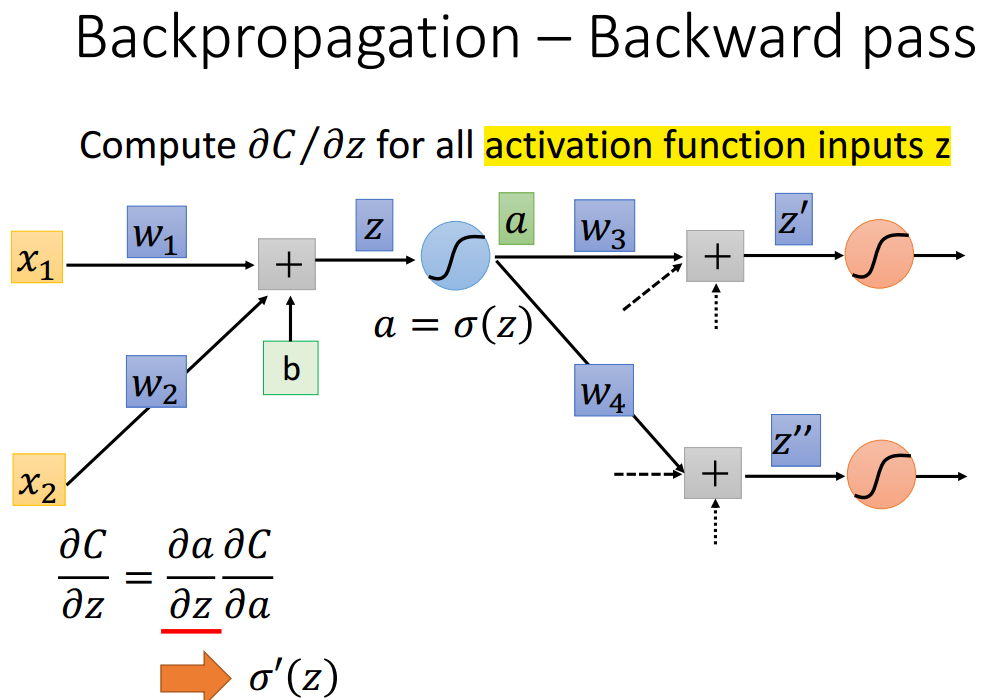
计算包含两部分,一个是激活函数本身的导数,对于一个固定结构的神经网络,sigma(z)的导数是小于0的,非常小,这点导致了梯度消散的问题。
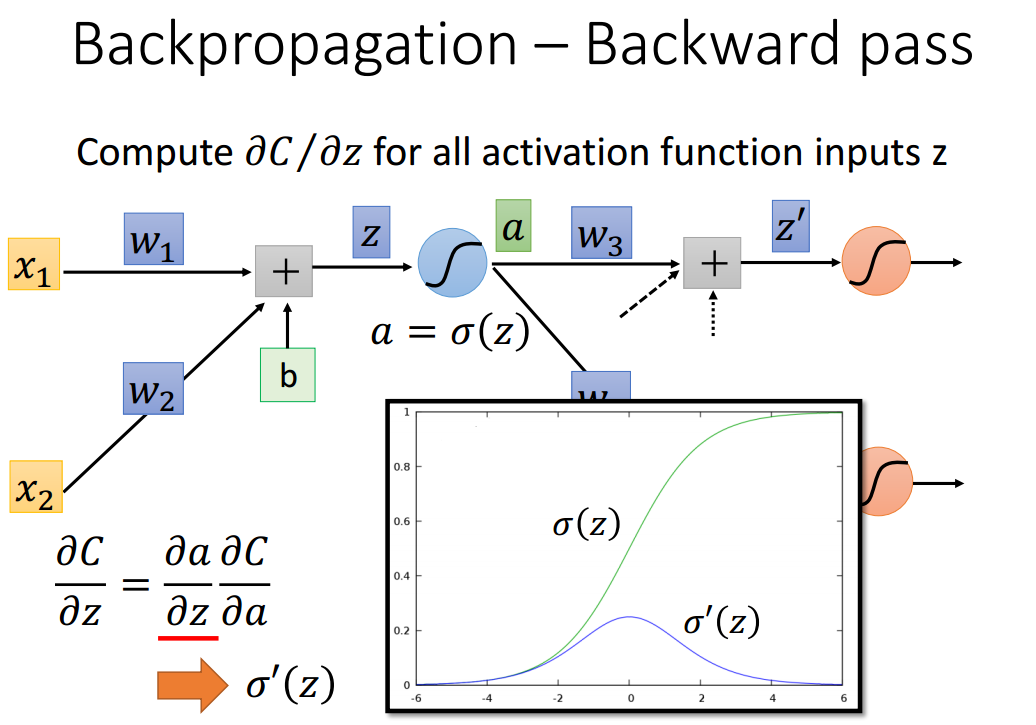
而损失函数L对a的导数则可以通过链式法则得到。其中W是已知的,只需要计算C与Z'和Z''的导数。
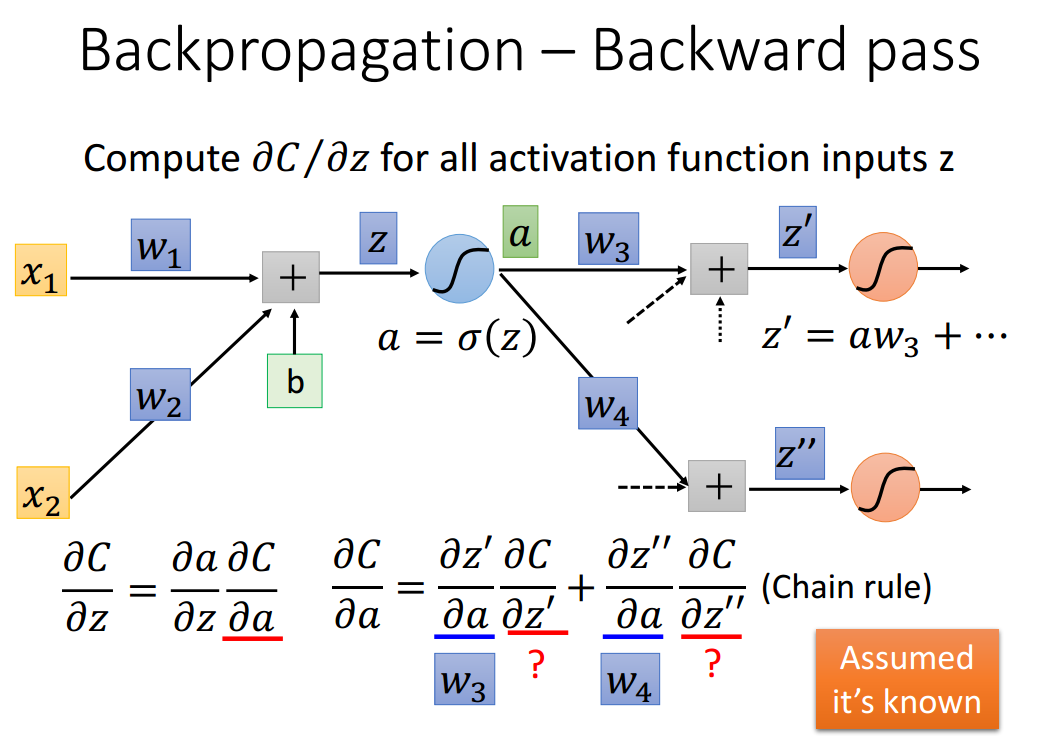
进一步归纳如下:
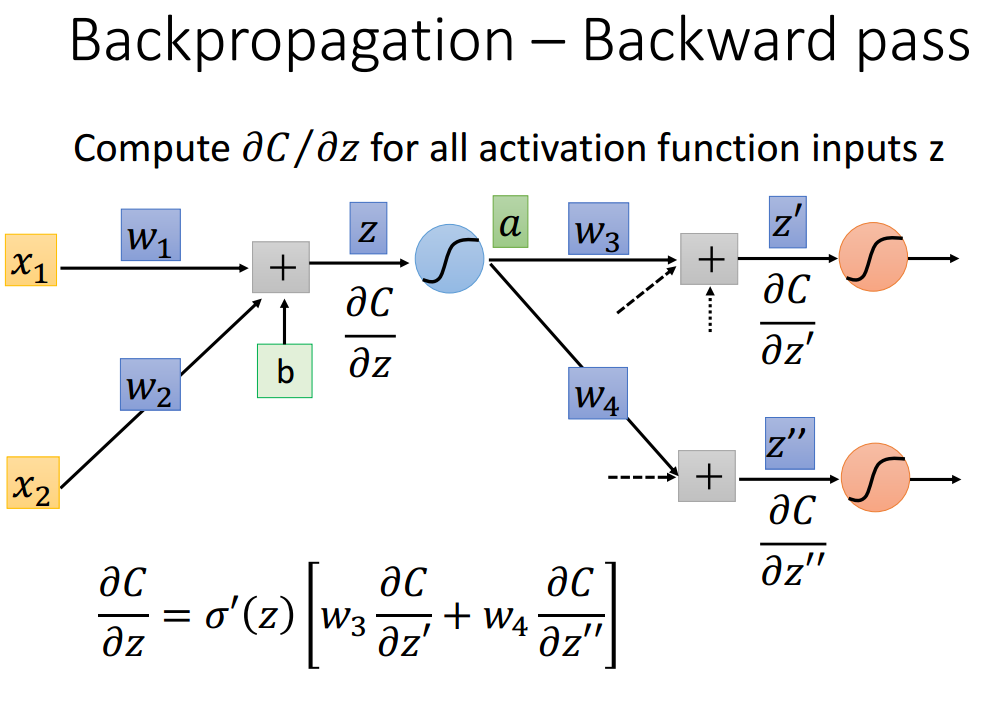
首先sigma(z)的导数是常数,只需要计算C与Z'和Z''的导数.
记住C对z的导数结构,递归执行这个结构得到所有的结果,例如C对z'的导数仍然是这个结构。
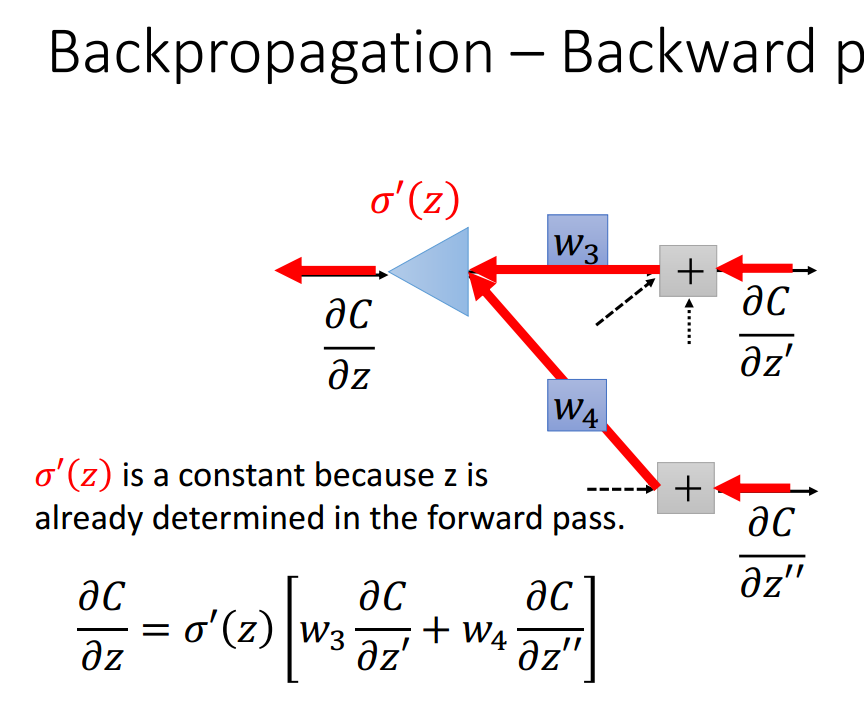
记住C对z的导数结构,递归执行这个结构得到所有的结果,例如C对z'的导数仍然是这个结构。
如何计算C与Z'和Z''的梯度?第一种情况,该计算发生在输出层,十分好计算。
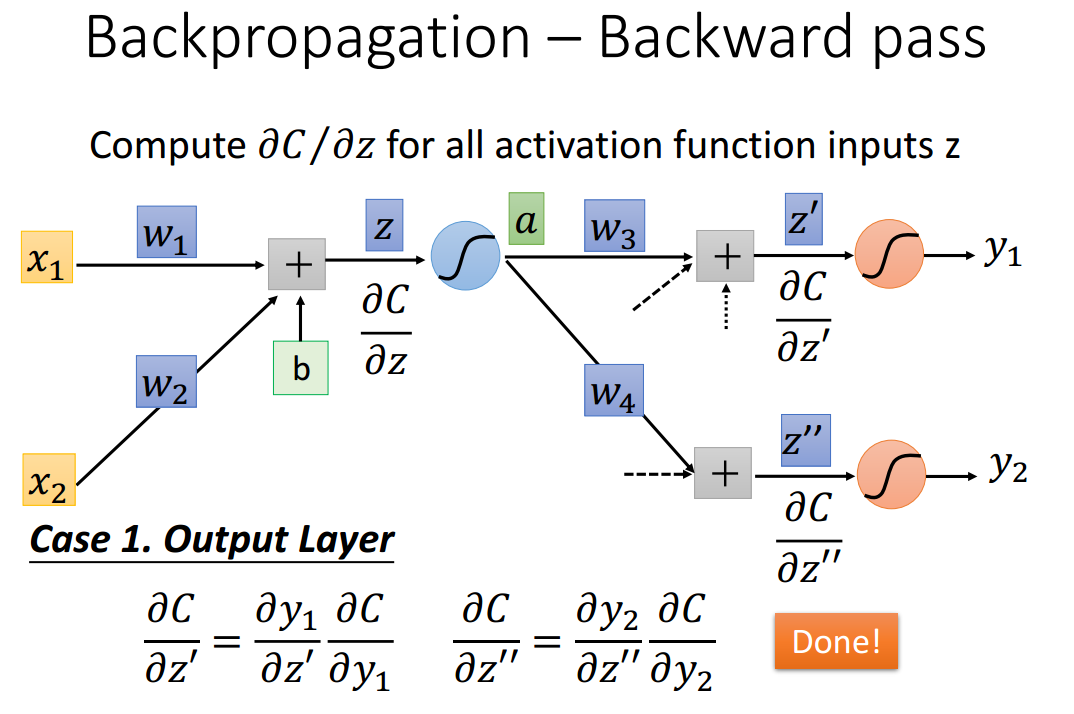
如何计算C与Z'和Z''的梯度?第二种情况,该计算发生在非输出层。
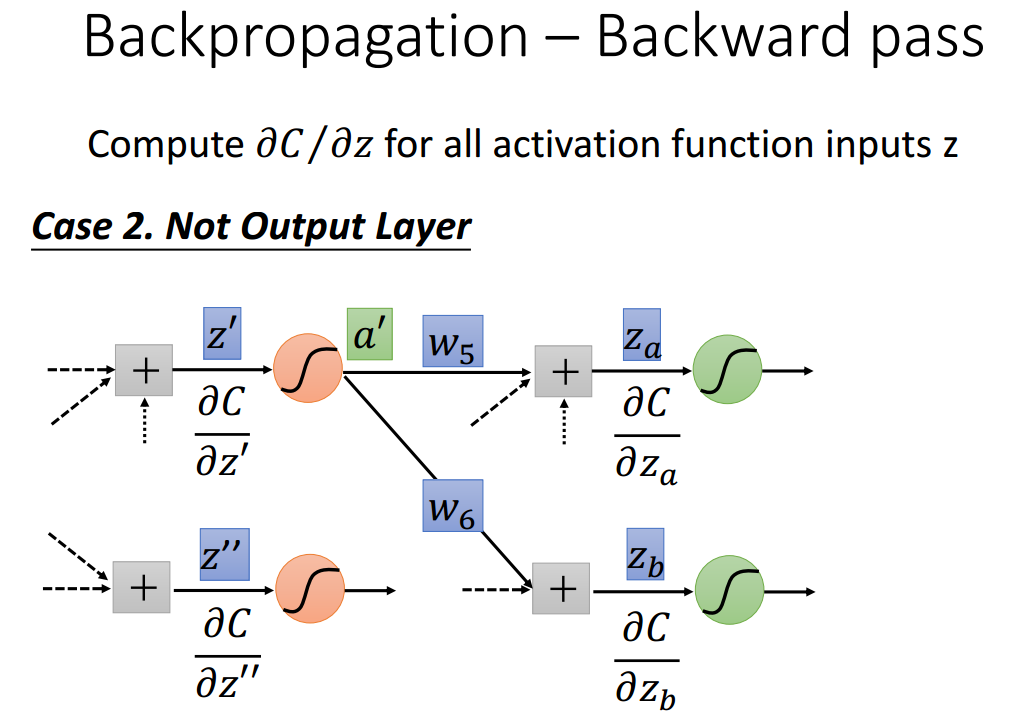
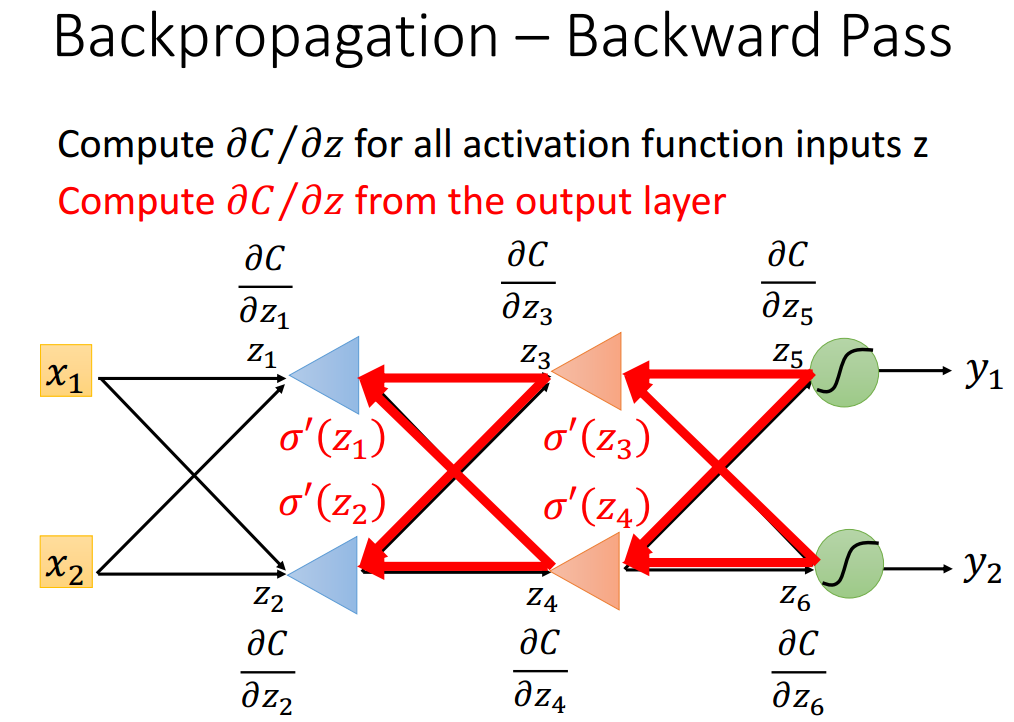
进行递归形式的计算即可,直至递归至输出层.
例如下图中z'的导数,就是由后面两条红色线的路径结果得到。其格式与下列公式相同:

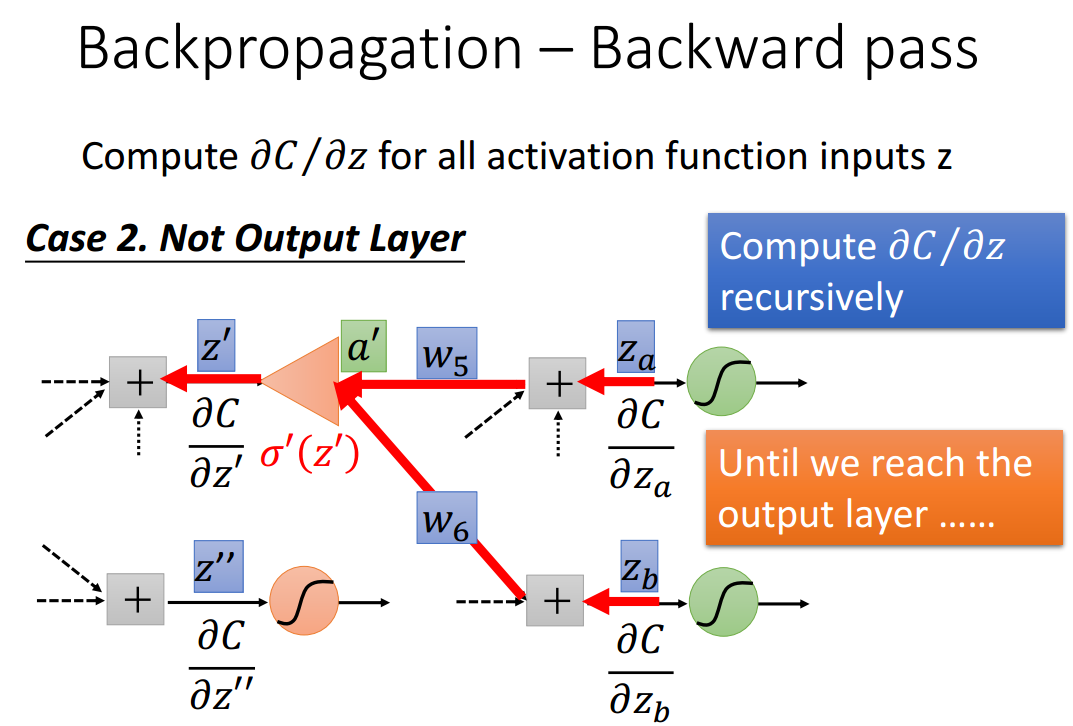
计算损失函数C与所有激活函数输入Z的导数。递归地从输出层开始计算
最后将两部分结合到一起,得到损失函数与W的梯度。
这里面会出现一个问题:在隐层中a是0到1的数,C对z的导数中,导函数的值是0到0.2的值,不断的连乘,得到的结果就是梯度太小,出现梯度消失的问题。
总结:
其实,网络中就有两个函数:
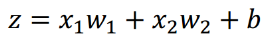
和激活函数:
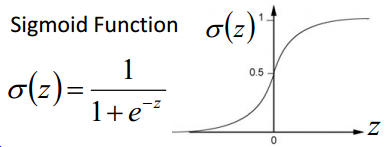
所以,在求导的时候,要先对z求导,然后对w求导。这中间用到了链式法则。
为了求得神经网络的最优系数,我们需要使用梯度下降算法。而梯度下降算法中的梯度需要通过前向传播算法和后向传播算法共同计算。神奇的是梯度需要计算的值非常少(大多数已知),所以速度非常快。
看到一个比较直观的后向传播介绍:
链接:https://www.zhihu.com/question/27239198/answer/89853077
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
简单的理解,它的确就是复合函数的链式法则,但其在实际运算中的意义比链式法则要大的多。
要回答题主这个问题“如何直观的解释back propagation算法?” 需要先直观理解多层神经网络的训练。
机器学习可以看做是数理统计的一个应用,在数理统计中一个常见的任务就是拟合,也就是给定一些样本点,用合适的曲线揭示这些样本点随着自变量的变化关系。
深度学习同样也是为了这个目的,只不过此时,样本点不再限定为(x, y)点对,而可以是由向量、矩阵等等组成的广义点对(X,Y)。而此时,(X,Y)之间的关系也变得十分复杂,不太可能用一个简单函数表示。然而,人们发现可以用多层神经网络来表示这样的关系,而多层神经网络的本质就是一个多层复合的函数。借用网上找到的一幅图[1],来直观描绘一下这种复合关系。

其对应的表达式如下:
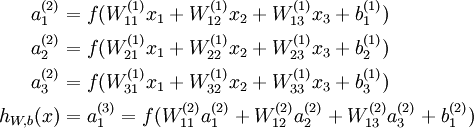
上面式的Wij就是相邻两层神经元之间的权值,它们就是深度学习需要学习的参数,也就相当于直线拟合y=k*x+b中的待求参数k和b。
和直线拟合一样,深度学习的训练也有一个目标函数,这个目标函数定义了什么样的参数才算一组“好参数”,不过在机器学习中,一般是采用成本函数(cost function),然后,训练目标就是通过调整每一个权值Wij来使得cost达到最小。cost函数也可以看成是由所有待求权值Wij为自变量的复合函数,而且基本上是非凸的,即含有许多局部最小值。但实际中发现,采用我们常用的梯度下降法就可以有效的求解最小化cost函数的问题。
梯度下降法需要给定一个初始点,并求出该点的梯度向量,然后以负梯度方向为搜索方向,以一定的步长进行搜索,从而确定下一个迭代点,再计算该新的梯度方向,如此重复直到cost收敛。那么如何计算梯度呢?
假设我们把cost函数表示为
我们以求e=(a+b)*(b+1)的偏导[3]为例。
它的复合关系画出图可以表示如下:
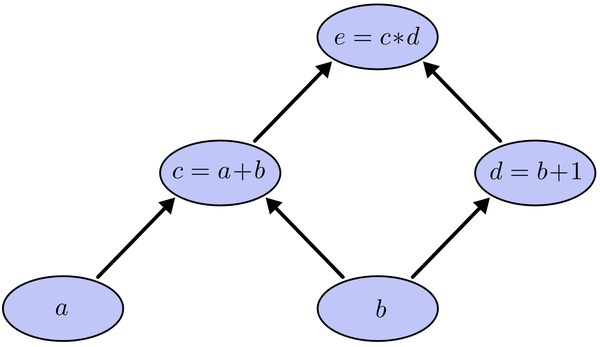
在图中引入了中间变量c,d。
为了求出a=2, b=1时,e的梯度,我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系,如下图所示:

利用链式法则我们知道:
链式法则在上图中的意义是什么呢?其实不难发现,
大家也许已经注意到,这样做是十分冗余的,因为很多路径被重复访问了。比如上图中,a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络,这样的冗余所导致的计算量是相当大的。
同样是利用链式法则,BP算法则机智地避开了这种冗余,它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
正如反向传播(BP)算法的名字说的那样,BP算法是反向(自上往下)来寻找路径的。
从最上层的节点e开始,初始值为1,以层为单位进行处理。对于e的下一层的所有子节点,将1乘以e到某个节点路径上的偏导值,并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后,第二层的每一个节点都“堆放"些值,然后我们针对每个节点,把它里面所有“堆放”的值求和,就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点,初始值设为顶点e对它们的偏导值,以"层"为单位重复上述传播过程,即可求出顶点e对每一层节点的偏导数。
以上图为例,节点c接受e发送的1*2并堆放起来,节点d接受e发送的1*3并堆放起来,至此第二层完毕,求出各节点总堆放量并继续向下一层发送。节点c向a发送2*1并对堆放起来,节点c向b发送2*1并堆放起来,节点d向b发送3*1并堆放起来,至此第三层完毕,节点a堆放起来的量为2,节点b堆放起来的量为2*1+3*1=5, 即顶点e对b的偏导数为5.
举个不太恰当的例子,如果把上图中的箭头表示欠钱的关系,即c→e表示e欠c的钱。以a, b为例,直接计算e对它们俩的偏导相当于a, b各自去讨薪。a向c讨薪,c说e欠我钱,你向他要。于是a又跨过c去找e。b先向c讨薪,同样又转向e,b又向d讨薪,再次转向e。可以看到,追款之路,充满艰辛,而且还有重复,即a, b 都从c转向e。
而BP算法就是主动还款。e把所欠之钱还给c,d。c,d收到钱,乐呵地把钱转发给了a,b,皆大欢喜。
------------------------------------------------------------------
【参考文献】
[1] 技术向:一文读懂卷积神经网络CNN
[2] Gradient
[3] http://colah.github.io/posts/2015-08-Backprop/
其他推荐网页:
1. tensorflow.org 的页面
2. Neural networks and deep learning



