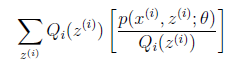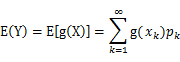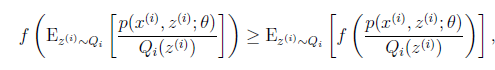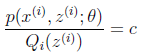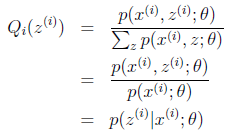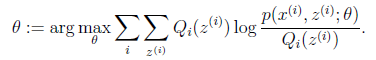EM算法(Expectation Maximization Algorithm)初探

1. 通过一个简单的例子直观上理解EM的核心思想

0x1: 问题背景

假设现在有两枚硬币Coin_a和Coin_b，随机抛掷后正面朝上/反面朝上的概率分别是

Coin_a：P1；1-P1
Coin_b：P2；1-P2

为了估计这个概率（我们事先是不知道这两枚硬币正面朝上的概率的），我们需要通过实验法来进行最大似然估计，每次取一枚硬币，连掷5下，记录下结果

硬币	结果	统计
Coin_a	正正反正反	3正-2反
Coin_b	反反正正反	2正-3反
Coin_a	正反反反反	1正-4反
Coin_b	正反反正正	3正-2反
Coin_a	反正正反反	2正-3反

根据最大似然估计的公式，可以很容易地估计出P1和P2，如下：

P1 = （3+1+2）/ 15 = 0.4
P2= （2+3）/10 = 0.5

这是我们基于现有的5次"观测结果"得到的最大似然估计，这是不是就是规律本身呢？答案是不知道！事实上，概率本身就是未知的，我们能做的只能是通过大量的实验去观测它。为了继续本例的讨论，我们假设P1=0.4；P2=0.5就是真实概率了

0x2: 加入隐变量

假设我么在抛掷硬币的时候被蒙上的眼睛而不知道每次抛掷的硬币是是Coin_a还是Coin_b，重新列出实验结果

硬币	结果	统计
Unknown	正正反正反	3正-2反
Unknown	反反正正反	2正-3反
Unknown	正反反反反	1正-4反
Unknown	正反反正正	3正-2反
Unknown	反正正反反	2正-3反

现在我们依然需要求P1、P2，但是怎么求？实验数据和Coin_a和Coin_b没法一一对应起来了。最大似然估计没法直接计算出来了

显然，此时我们多了一个隐变量z，它是一个5维的向量（z1，z2，z3，z4，z5），代表每次投掷时所使用的硬币（是Coin_a还是Coin_b），这个隐变量z不知道，就无法估计P1、P2。但要估计z，我们又得先知道P1、P2，根据最大似然思想基于P1、P2和实验观测数据估计z。我们似乎陷入了一个鸡生蛋蛋生鸡的死循环问题！

破题的核心思路在于：

我们先不管三七二十一，在所有可行解空间中随机初始化一个P1、P2，基于初始化的P1、P2来估计z，然后基于z按照最大似然概率法则去估计新的P1、P2
（1）如果新的P1、P2和我们初始化的初始值差距小于一个阈值，说明收敛了，我们初始化的P1、P2有很大可能就是真实值
（2）如果新的P1、P2和我们初始化的初始值差距很大，则继续用新的P1、P2进行迭代，重复本轮步骤，直至收敛

从算法思想上来说，这是深度神经网络中进行梯度下降逐步迭代求解最优解的思想很类似，我们无法在一开始知道全局最优值在什么地方，所以就随机初始化一个，然后在每轮的迭代中，逐渐求解局部最优值，不断尝试考虑全局最优值

0x3: EM初级版

我们先给P1和P2随机化地赋一个初始值，例如

Coin_a P1 = 0.1; 1-P1 = 0.9
Coin_b P2 = 0.8; 1-P2 = 0.2

基于这个假设的概率P1、P2，我们根据实验观测结果来计算每一轮抛掷的最可能是哪个硬币（即求z值）

轮数	硬币Coin_a的概率	硬币Coin_b的概率	本轮最可能的硬币
1	0.1 * 0.1 * 0.1 * 0.9 * 0.9 = 0.00081（3正2反）	0.8 * 0.8 * 0.8 * 0.2 * 0.2 = 0.02048（3正2反）	Coin_b
2	0.1 * 0.1 * 0.9 * 0.9 * 0.9 = 0.00729（2正3反）	0.8 * 0.8 * 0.2 * 0.2 * 0.2 = 0.00512（2正3反）	Coin_a
3	0.1 * 0.9 * 0.9 * 0.9 * 0.9（1正4反）	0.8 * 0.2 * 0.2 * 0.2 * 0.2 = 0.00512（1正4反）	Coin_a
4	0.1 * 0.1 * 0.1 * 0.9 * 0.9（3正2反）	0.8 * 0.8 * 0.8 * 0.2 * 0.2 = 0.02048（3正2反）	Coin_b
5	0.1 * 0.1 * 0.9 * 0.9 * 0.9 = 0.00729（2正3反）	0.8 * 0.8 * 0.2 * 0.2 * 0.2 = 0.00512（2正3反）	Coin_a

按照最大似然法则：

第1轮中最有可能的是硬币Coin_b
第2轮中最有可能的是硬币Coin_a
第3轮中最有可能的是硬币Coin_a
第4轮中最有可能的是硬币Coin_b
第5轮中最有可能的是硬币Coin_a

我们把上面的值作为本轮z的估计值，然后按照最大似然概率法则来重新估计P1、P2（这时已知每轮的硬币类型了，可以直接根据观测结果估计概率）

Coin_a P1 = （2 + 1 + 2）/ 15 = 0.33333：抛了3轮，每轮5次，总计15次
Coin_b P1 = （3 + 3）/ 10 = 0.6：抛了2轮，每轮5次，总计10次

对比下我们初始化的P1和P2和新估计出的P1和P2

	Coin_a P1	Coin_b P2
初始化的概率值	0.1	0.8
本轮估计出的概率值	0.3333	0.6
真实的概率值	0.4	0.5

可以看到，我们本轮的P1、P2估计值相比于它们的初始值，更接近于它们各自的真实值了，即在向全局最优靠近

我们只要继续按照上面的迭代过程，用估计出的P1、P2继续估计z，再用z来估计新的P1、P2，反复迭代下去，就可以最终收敛得到P1=0.4、P2=0.5这个真实值了，此时无论怎么继续迭代，P1、P2都会保持不变，此时我们就得到了P1、P2的最大似然估计

很明显这里有2个问题：

1. 为啥新估计出的P1、P2会更加接近真实值？只是本例的偶然吗？答案是否定的，我们接下来的章节会介绍理论数学推导来证明EM的单调性
2. 不管我们如何初始化，迭代一定会收敛到真实的P1、P2吗？答案是否定的，这取决于我们的P1、P2初始化值，EM对初始值比较敏感，因为它很容易陷入到局部最优

0x4: EM进阶版

回想一下我们上面用最大似然概率法则估计出的z值，然后再用z值按照最大似然法则估计新的P1、P2。但是我们估计z值的时候只取了最可能的那个z值，而另一个z值也许只是概率上差了很少的一点，这部分的概率就被我们忽略了，这种求解方式不够"柔和"，我们可以改进一下

如果考虑所有可能的z值，对每一个z值都估计出一个新的P1、P2，将每一个z值概率大小作为权重，将所有新的P1、P2分别加权相加，这样的P1、P2收敛性应该会更好一些

为了保持连贯性，我们复制上面的表格计算结果（在假设初始值P1、P2的前提下计算每轮z是Coin_a和Coin_b的概率）

轮数	硬币Coin_a的概率	硬币Coin_b的概率
1	0.1 * 0.1 * 0.1 * 0.9 * 0.9 = 0.00081（3正2反）	0.8 * 0.8 * 0.8 * 0.2 * 0.2 = 0.02048（3正2反）
2	0.1 * 0.1 * 0.9 * 0.9 * 0.9 = 0.00729（2正3反）	0.8 * 0.8 * 0.2 * 0.2 * 0.2 = 0.00512（2正3反）
3	0.1 * 0.9 * 0.9 * 0.9 * 0.9 = 0.06561（1正4反）	0.8 * 0.2 * 0.2 * 0.2 * 0.2 = 0.00128（1正4反）
4	0.1 * 0.1 * 0.1 * 0.9 * 0.9 = 0.00081（3正2反）	0.8 * 0.8 * 0.8 * 0.2 * 0.2 = 0.02048（3正2反）
5	0.1 * 0.1 * 0.9 * 0.9 * 0.9 = 0.00729（2正3反）	0.8 * 0.8 * 0.2 * 0.2 * 0.2 = 0.00512（2正3反）

然后计算每轮Coin_a和Coin_b各自概率的权重

轮数	硬币Coin_a的权重	硬币Coin_b的概率
1	0.00081 / (0.00081 + 0.02048) = 0.0380460310005	0.961953969
2	0.00729 / (0.00729 + 0.00512) = 0.587429492345	0.412570507655
3	0.06561/ (0.06561+ 0.00128) = 0.980864105247	0.0191358947526
4	0.00081 / (0.00081 + 0.02048) = 0.0380460310005	0.961953969
5	0.00729 / (0.00729 + 0.00512) = 0.587429492345	0.412570507655

相比于简易版EM，我们此时更加谨慎合理，我们对于第一轮的只能说有0.038的概率是Coin_a，有0.96的概率是Coin_b，不再是非彼既此。这样我们在估计P1、P2的时候，就可以用上全部的观测数据，而不仅仅是部分数据

这一步，我们实际估计出了z的概率分布，这步被称为E步

有了z的概率分布，我们根据观测数据进行最大似然估计

硬币	结果	统计
Unknown	正正反正反	3正-2反
Unknown	反反正正反	2正-3反
Unknown	正反反反反	1正-4反
Unknown	正反反正正	3正-2反
Unknown	反正正反反	2正-3反

根据权重对P1、P2进行最大似然估计，计算过程中得到P1、P2的概率分布

轮数	Coin_a P1（正面）	Coin_a 1-P1（反面）	Coin_b P2（反面）	Coin_b 1-P2（反面）
1	0.0380460310005 * 3 = 0.114138093001	0.0380460310005 * 2 = 0.076092062001	0.961953969 * 3 = 2.885861907	0.961953969 * 2 = 1.923907938
2	0.587429492345 * 2 = 1.17485898469	0.587429492345 * 3 = 1.76228847703	0.412570507655 * 2 = 0.82514101531	0.412570507655 * 3 = 1.23771152296
3	0.980864105247 * 1 = 0.980864105247	0.980864105247 * 4 = 3.92345642099	0.0191358947526 * 1 = 0.0191358947526	0.0191358947526 * 4 = 0.0765435790104
4	0.114138093001	0.076092062001	2.885861907	1.923907938
5	1.17485898469	1.76228847703	0.82514101531	1.23771152296
总计	3.55885826063	7.60021749905	7.44114173937	6.39978250093

Coin_a P1 = 3.55885826063 / (3.55885826063 + 7.60021749905) = 0.318920521491
Coin_b P1 = 7.44114173937 / (7.44114173937 + 6.39978250093) = 0.53761884757

对比下我们初始化的P1和P2和新估计出的P1和P2

	Coin_a P1	Coin_b P2
初始化的概率值	0.1	0.8
EM初级版估计出的概率值	0.3333	0.6
EM高级版估计出的概率值	0.318920521491	0.53761884757
真实的概率值	0.4	0.5

这一步中，我们根据E步中求出的z的概率分布，依据最大似然概率法则去估计P1、P2，被称为M步。如下图

从图中可以看到几点

1. 初始的第一步是原始的最大似然估计要求的参数，我们通过随机初始化的方式赋予了一个随机初始值
2. Expectation这一步的目的是估计出隐变量的概率分布
3. Maximization这一步就是原始的最大似然概率估计（基于本轮Expectation得到的隐变量概率分布），估计出模型的参数

Relevant Link:

https://www.zhihu.com/question/27976634
http://blog.sina.com.cn/s/blog_a7da5cda010158b3.html
http://www.cnblogs.com/Gabby/p/5344658.html
http://blog.csdn.net/livecoldsun/article/details/40833829

2. EM算法的引入

EM算法是一种迭代算法，1977年由Dempster等人总结提出，用于含有隐变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每轮迭代由两步组成：E步（求期望 expectation）；M步（求极大似然），所以这一算法称为期望极大算法（expectation maximization algorithm EM算法）

概率模型有时既含有观测变量（observable variable），又含有隐变量或潜在变量（latent variable）。如果概率模型的变量都是观测变量，那么给定训练观测数据，可以直接用极大似然估计法或贝叶斯估计法（带先验概率的极大似然估计）来估计模型参数。但是，当模型含有隐变量时，就不能简单地使用这些估计方法（即我们无法直接求出解析解），EM算法就是针对含有隐变量的概率模型参数的极大似然估计法或极大后验概率估计法

0x1: EM算法数学定义

输入：观测变量数据Y，隐变量数据Z，联合概率密度分布，条件分布

一般地，用Y表示观测随机变量的数据，Z表示隐随机变量的数据，Y和Z合在一起称为完全数据（complete-data），观测数据Y单独称为不完全数据（incomplete-data）

输出：需要估计的模型参数

（1）随机初始化模型参数的初值，开始迭代。模型参数的初值可以任意随机选择，但需要注意EM算法对初值很敏感（EM每轮迭代都是在求局部最优，并不能保证最后得到全局最优解）

（2）E步：记为第 i 次迭代参数的估计值，在第 i + 1 次迭代的E步，计算：，这里，是在给定观测数据Y和当前的参数估计下隐变量数据Z的条件概率分布。

注意，是EM算法的核心，称为Q函数（Q function）

完全数据的对数似然函数关于在给定观测数据Y和当前模型参数下对未观测隐变量Z的条件概率分布的期望称为Q函数：

E步求Q函数，Q函数式中Z是未观测数据，Y是观测数据，可以看到，Q函数是为M步进行最大似然估计做数学公式解析准备的，每轮迭代实际上是在求Q函数机器极大。即EM的迭代是不断调整隐变量的极大似然值，使其（隐变量）接近真实值，可以预见，只有隐变量越接近真实值，模型参数的极大似然才能随着不断接近真实值

（3）M步：求使极大化的（模型参数），确定第 i + 1次迭代的参数的估计值。每次迭代使模型参数的似然函数增加或达到局部极值

（4）重复（2）和（3）步，直至收敛，收敛停止条件一般是对较小的正数，若满足（及本轮相较于上一轮的优化幅度小于一定阈值）则停止迭代

0x2: 举一个实际的例子说明EM算法的推导

例如我们有一些东北人的身高的数据，又知道身高的概率模型是高斯分布，那么利用极大化似然函数的方法可以估计出高斯分布的两个参数：均值和方差（已知模型和数据估计出模型参数），这是基本的最大似然概率估计的方法过程。但是我们面临的是这种情况，我手上的数据是四川人和东北人的身高合集，然而对于其中具体的每一个数据，并没有标定出它来自“东北人”还是“四川人”，如果把这个数据集的概率密度画出来，大约是这个样子：

我们来具体考虑一下上面这个问题，我们能不能继续用极大似然估计，我们尝试写出我们需要极大化的似然函数：，m代表Xi的类别，这里是2（四川、东北），代表样本类型Xi和模型参数的联合概率密度，然而问题就在我们并不知道的解析表达式

通过贝叶斯边缘概率分布定理，将上式改写为包含隐变量 Z 的公式：

上式同时有两个未知量，我们没法同时进行似然估计，EM解决的方法是假设，首先初始化假设一个模型参数 θ，然后每个样本来自四川/东北的P(Zi)的概率分布就可以算出来了。P（x_i，z_{i；θ为某个常数}）= P（x_i| z_i）P（z_i），左式中 x|z=0服从四川人分布，x|z=1服从东北人分布，所以最隐变量 Z 的似然函数P（z_i）可以写成含有θ的函数，通过极大化它我们可以得到一个新的θ。新的θ因为考虑了样本来自哪个分布，会比原来的θ估计更能反映数据本身的规则（所有算法的本质都是在反映数据本身的规律）。在下一轮迭代中，我们基于这个更好的θ再对每个样本重新估计它来自四川和东北的最大似然概率（即P（z_i）），用更好的θ算出来的概率会更准确，如果不断循环下去知道收敛

纯理论上，上面说的就是EM算法了，但是工程化起来非常困难，主要原因是我们要极大化的似然函数有"和的log"这一项，log里是一个和的形式，求导起来非常困难，这导致我们希望直接求解析解的目的变得十分困难，需要消耗非常大的计算量（如果这里是计算机实现可能也不是大问题）

为了解决这个问题，EM的创造者采取了一个折衷的方法：我不能一次性得到极大值（上界），但是我能求得下界，并保证每轮迭代下界都在不断提高，那么从总体看，上界也是在被动地逐轮提高了

所以问题变成了：如何得到每一轮参数最大似然函数的下界，这就需要用到Jensen不等式：X是一个随机变量，f(X)是一个凸函数（二阶导数大或等于0），那么有

，当且仅当X是常数的时候等号成立，如果f（X）是凹函数，不等号反向

log函数是凹函数，所以E（f(x)） <= f（E(x)）

这里我们需要说明下为什么Jensen不等式能保证每轮迭代上界是在不断提高的，看下图

横坐标是参数，纵坐标是似然函数

1. 首先我们初始化一个θ1，根据它求似然函数一个紧的下界，也就是图中第一条黑短线，黑短线上的值虽然都小于似然函数的值，但至少有一点可以满足等号（所以称为紧下界），最大化小黑短线我们就hit到至少与似然函数刚好相等的位置，对应的横坐标就是我们的新的θ2
2. 如此进行，只要保证随着θ的更新，每次最大化的小黑短线（Jensen不等式的下界）值都比上次的更大，那么算法收敛，最后就能最大化到似然函数的极大值处

所以问题从难以求解析解的上界（原模型参数的最大似然函数）转化为了求下界。为了构造这个小黑短线（下界），就要靠Jensen不等式，注意到我们这里的log函数是一个凹函数，所以我们使用Jensen不等式的凹函数版本，即代表了我们原函数最大似然函数，它就是上界，我们要想办法写出不等式右边的，它代表了下界。

所以，现在问题来了，我们的似然函数和数学期望有什么关系？一眼看上去没啥关系，这就我们做一些公式变形，我们需要把log里面的东西写成一个数学期望的形式，注意到log里的和是关于隐变量Z的和，于是自然而然，这个数学期望一定是和Z有关，如果设Q(z)是Z的分布函数，那么可以这样构造：

1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式，考虑到是凹函数（二阶导数小于0），而且

其实就是的期望

先看看下列关于数学期望的公式定义：

设Y是随机变量X的函数（g是连续函数），那么

（1） X是离散型随机变量，它的分布律为，k=1,2,…。若绝对收敛，则有

（2） X是连续型随机变量，它的概率密度为，若绝对收敛，则有

对应于上述问题

（1）Y是

（2）X是

（3）是

（4）g是到的映射。这样解释了式子（2）中的期望，再根据凹函数时的Jensen不等式：

可以得到（3），可以看到，Jensen不等式把"和的log"转化为了"log的和"，使求解难度下降了

这个过程可以看作是对求了下界，但是我们前面说了，我们希望Jensen不等式的为等号，说明我们找到了Qi的局部最优值

根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

c为常数，不依赖于。对此式子做进一步推导，我们知道，那么也就有，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式：

至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。接下来的M步，就是在给定后，调整，去极大化的下界（在固定后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：

循环重复直到收敛 {

（E步）对于每一个i，计算

（M步）计算

Relevant Link:

http://blog.csdn.net/yzheately/article/details/51164441
http://www.cnblogs.com/yymn/p/4769736.html
http://blog.csdn.net/xiaozezepingping/article/details/29849007
http://blog.csdn.net/livecoldsun/article/details/40833829
http://www.cnblogs.com/Gabby/p/5344658.html

3. EM算法的收敛性

上一章节，我们通过Jensen不等式，解决了EM算法中最大似然函数估计中"和的对数"求导困难问题，即通过Jensen不等式将其转化为求其下界，并证明了Jensen不等式等号成立的条件正好就是对隐变量求其最大后验概率.所以接下来的问题就是EM算法能保证每轮迭代中下界会不断提高并收敛吗？如果收敛，是否收敛到全局最大值或局部极大值

0x1: 定理1 - EM对模型参数的最大似然估计是单调递增的

设为观测数据的似然函数，为EM算法得到的参数估计序列（每轮迭代的最大似然参数估计结果），为对应的似然函数序列，则是单调递增的，即，下面证明这一点

由于：，取对数有：

可以看到，式子等号右边的左半部分就是Q函数：

而等号右边的右半部分我们设：

于是对数似然函数可以写成：

对上式分别取为和并相减，有：

只需证明上式等号右边是非负的即达到我们的目的

（1）上式等号右边第一项，由于使达到极大，所以有

（2）上式等号右边第二项展开得：

该公式推导解释如下

1. 等号由Jensen不等式得到
2. 最后一步等于0是因为Z是已知的，概率为1，log = 0
3. 倒数第二步的分母约分根据条件概率边缘分布原理

以上推导证明

Relevant Link:

http://blog.csdn.net/xiaozezepingping/article/details/29849007
http://blog.csdn.net/yzheately/article/details/51164441
http://www.cnblogs.com/yymn/p/4769736.html

4. EM算法在高斯混合模型（GMM）学习中的应用

EM算法的一个重要应用是高斯混合模型的参数估计，高斯混合模型应用广泛，在许多情况下，EM算法是学习高斯混合模型（Gaussian misture model）的有效方法

0x1: 高斯混合模型定义

高斯混合模型是指具有如下形式的概率分布模型：，其中，是系数，是高斯分布密度，为高斯模型参数，称为第k个分模型（联想到adaboost中的加法模型，高斯混合模型本质上也是分模型的线性组合）

0x2: 高斯混合模型参数估计中的EM的算法

假设观测数据y1，y2，....，yn由高斯混合模型生成，，其中，，我们用EM算法估计高斯混合模型的参数

既然要用EM算法来进行高斯混合模型的参数估计，我们就需要将高斯混合模型改写成包含隐变量和观测量的公式，并且构造完全数据的似然函数，套用E和M步的求解过程

1. 明确隐变量，写出完全数据的对数似然函数

可以设定观测数据 y1，y2，....，yn 是这样产生的：

（1）首先按照概率选择第 k 个高斯分布模型；

（2）然后依照第 k 个分模型的概率分布生成观测数据。这是观测数据，是已知的；

（3）反映观测数据来自第 k 个分模型的数据是未知的（隐变量），，以隐变量表示，其定义如下：，其中是0-1随机变量

有了观测数据及未观测数据，那么完全数据是，于是可以写出完全数据的似然函数：

式中，，则完全数据的对数似然函数为：

2. EM算法的E步：确定Q函数

这里需要计算，记为

是在当前模型参数下第 j 个观测数据来自第 k 个分模型的概率，称为分模型 k 对观测数据的响应度

将及代入上式得：

3. 确定EM算法的M步

迭代的M步是求函数对的极大值，即求新一轮迭代的模型参数：，和最大似然估计一样，还是求偏导求极值点的思路，用表示的各参数

（1）分别对求偏导数并令其为0：

（2）求是在条件下求偏导数并令其为0得到的：，可以看到，对隐变量其实就是在进行最大似然估计

重复以上计算，知道对数似然函数值不再有明显变化为止

Relevant Link:

http://www.cnblogs.com/xingshansi/p/6584555.html
http://www.cnblogs.com/mindpuzzle/archive/2013/04/24/3036447.html

5. EM算法在思想上和K-means的异同点

0x1: 简单回顾K-means算法

k-means算法是一种得到最广泛使用的聚类算法。它是将各个聚类子集内的所有数据样本的均值作为该聚类的代表点。k-means 计算过程：

1. 随机选择k个类簇的中心
2. 计算每一个样本点到所有类簇中心的距离，选择最小距离作为该样本的类簇
3. 重新计算所有类簇的中心坐标，直到达到某种停止条件(迭代次数/簇中心收敛/最小平方误差)

从直观上我们感觉K-means的步骤2和步骤3就是EM算法的E和M步，下面我们通过数学推导来证明这一点

0x2: K-means算法是EM算法的一个特例数学证明

聚类问题：给定N个数据点 $x_1, x_2, \ldots, x_N \in \mathbb{R}^m$ ，给定分类数目 $K$ （需人工设定带聚类数目K），求出 $K$ 个类中心 $\mu_1, \mu_2, \ldots, \mu_K \in \mathbb{R}^m$ ，使得所有点到距离该点最近的类中心的距离的平方和 $\sum_{i=1}^N{\min_{1\le k \le K} ||x_i-\mu_k||_2^2}$ 最小

含隐变量的最大似然问题：给定数据点 $x_1, x_2, \ldots, x_N \in \mathbb{R}^m$ ，给定分类数目 $K$ ，考虑如下生成模型，

$p(x,z|\mu_1, \mu_2, \ldots, \mu_K)\propto \begin{cases} \exp\left(-\left|\left|{x-\mu_z}\right|\right|_2^2\right) & ||x-\mu_z||_2=\min_{1\le k \le K} ||x-\mu_k||_2\\ 0 & ||x-\mu_z||_2>\min_{1\le k \le K} ||x-\mu_k||_2 \\ \end{cases}$

模型中 $z\in\{1,2,\ldots,K\}$ 为隐变量

这个式子的直观意义是这样的：对于某个将要生成的点 $x$ 和他的类别号 $z$ ，如果不满足“ $x$ 到中心 $\mu_z$ 的距离小于等于 $x$ 到其他中心 $\mu_k$ 的距离”的话，则不生成这个点。如果满足的话，则 $z$ 取值就是这个“最近的”类中心的编号（如果有多个则均等概率随机取一个），以高斯的概率密度在这个类中心周围生成点 $x$

回想我们第一章举的那个例子：

K-means的这种方法相当于进行了"硬分类"，每个样本点有且只能在一个类别Z中，而不能具有概率分布

用EM算法解这个含隐变量的最大似然问题就等价于用K-means算法解原聚类问题

E步骤 - 根据当前质心求样本的分类最大似然结果Zi：

1、计算 $p(z_i|x_i,\{\mu_k\}^{(t)})\propto \begin{cases} 1 & ||x_i-\mu_{z_i}^{(t)}||_2=\min_{1\le k \le K} ||x_i-\mu_k^{(t)}||_2\\ 0 & ||x_i-\mu_{z_i}^{(t)}||_2>\min_{1\le k \le K} ||x_i-\mu_k^{(t)}||_2 \\ \end{cases}$ ，以及 $p(Z|X,\{\mu_k\}^{(t)})=\prod _{i=1}^N p(z_i|x_i,\{\mu_k\}^{(t)})$ （联合概率），这里使用正比于符号是考虑到距离点 $x_i$ 最近的类中心可能不止一个，下面推导假设类中心点只有一个，并且该类中心的编号为 $y_i$

2、计算目标函数 $Q(\{\mu_k\}|\{\mu_k\}^{(t)})=\mathbb{E}_{Z|X,\{\mu_k\}^{(t)}}\left[\log p(X,Z|\{\mu_k\})\right]$ $=\sum_{i=1}^{N}\mathbb{E}_{z_i|x_i,\{\mu_k\}^{(t)}}\left[\log p(x_i,z_i|\{\mu_k\})\right]$ $=\sum_{i=1}^{N}\log p(x_i,z_i=y_i|\{\mu_k\})$ $= const - \sum_{i=1}^{N}\left|\left|{x_i-\mu_{y_i}}\right|\right|_2^2$

因为我们的重点是 $\{\mu_k\}$ 的值，而不是目标函数本身的值，因此可以将目标函数替换为， $Q'(\{\mu_k\}|\{\mu_k\}^{(t)})= \sum_{i=1}^{N}\left|\left|x_i-\mu_{y_i}\right|\right|_2^2$ ，并把求最大值转换为求最小值。

注意到这里 $\{y_i\}_{i=1}^N$ 其实是根据当前参数 $\{\mu_k\}^{(t)}$ 求出来的，而且这个目标函数的已经是K-means的目标函数了。

EM算法中E步对隐变量 Zi 求其最大似然值，这等价于K-means算法中对于每一个点 $x_i$ 找当前最近的聚类中心 $\mu_{y_i}$

M步骤 - 重新寻找新的质心：
找寻 $\{\mu_k\}$ 使得 $Q'(\{\mu_k\}|\{\mu_k\}^{(t)})$ 最小。

将指标集 $\{1,2,\ldots,K\}$ 割为 $K$ 个， $I_k=\{i|y_i=k\}$ ，则 $Q'(\{\mu_k\}|\{\mu_k\}^{(t)})= \sum_{k=1}^{K}\sum_{i\in I_k}\left|\left|\mu_k-x_i\right|\right|_2^2$

由于求和的每一项都是非负的，所以当每一个内层求和 $\sum_{i\in I_k}\left|\left|\mu_k-x_i\right|\right|_2^2$ 都达到最小时，总和 $Q'(\{\mu_k\}|\{\mu_k\}^{(t)})$ 最小。

此时 $\mu_k=\sum_{i\in I_K} \frac{x_i}{\left|I_K\right|}$ ，即求平均值

这和K-means算法中根据当前分配求新的聚类中心的操作是一样的

0x3: k-means算法与由EM算法推导出的的关系

1. k-means是两个步骤交替进行，可以分别看成E步和M步；
2. M步中将每类的中心更新为分给该类各点的均值，可以认为是在「各类分布均为单位方差的高斯分布」的假设下，最大化似然值；
3. E步中将每个点分给中心距它最近的类（硬分配），可以看成是EM算法中E步（软分配）的近似。

k-means对GMM的简化有

$\pi_k = 1/K$ ，混合权重相等
$\Sigma_k = \epsilon I$ ，各个分模型的协方差相等，且固定为单位矩阵的倍数
$x_n$ 分配给各个分模型的方式，由基于概率分布变为winner-take-all方式的 hard 赋值

所以说GMM是更为flexible的model，由于大量的简化，使得k-means算法收敛速度快于GMM，并且通常使用k-means对GMM进行初始化

Relevant Link:

http://www.cnblogs.com/arachis/p/KMeans.html 
https://www.zhihu.com/question/49972233
http://www.cnblogs.com/mindpuzzle/archive/2013/04/24/3036447.html

6. EM算法在高斯混合模型(GMM)学习中的应用

EM算法的一个重要应用是高斯混合模型的参数估计

0x1: 利用GMM进行无监督聚类

类似于K-means，GMM可以用来对鸢尾花这种具有特征空间区分的数据集进行无监督聚类

# -*- coding:utf-8 -*-

import matplotlib as mpl
import matplotlib.pyplot as plt

import numpy as np

from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import StratifiedKFold

print(__doc__)

colors = ['navy', 'turquoise', 'darkorange']


def make_ellipses(gmm, ax):
    for n, color in enumerate(colors):
        if gmm.covariance_type == 'full':
            covariances = gmm.covariances_[n][:2, :2]
        elif gmm.covariance_type == 'tied':
            covariances = gmm.covariances_[:2, :2]
        elif gmm.covariance_type == 'diag':
            covariances = np.diag(gmm.covariances_[n][:2])
        elif gmm.covariance_type == 'spherical':
            covariances = np.eye(gmm.means_.shape[1]) * gmm.covariances_[n]
        v, w = np.linalg.eigh(covariances)
        u = w[0] / np.linalg.norm(w[0])
        angle = np.arctan2(u[1], u[0])
        angle = 180 * angle / np.pi  # convert to degrees
        v = 2. * np.sqrt(2.) * np.sqrt(v)
        ell = mpl.patches.Ellipse(gmm.means_[n, :2], v[0], v[1],
                                  180 + angle, color=color)
        ell.set_clip_box(ax.bbox)
        ell.set_alpha(0.5)
        ax.add_artist(ell)

iris = datasets.load_iris()

# Break up the dataset into non-overlapping training (75%) and testing
# (25%) sets.
skf = StratifiedKFold(n_splits=4)
# Only take the first fold.
train_index, test_index = next(iter(skf.split(iris.data, iris.target)))


X_train = iris.data[train_index]
y_train = iris.target[train_index]
X_test = iris.data[test_index]
y_test = iris.target[test_index]

n_classes = len(np.unique(y_train))

# Try GMMs using different types of covariances.
estimators = dict((cov_type, GaussianMixture(n_components=n_classes,
                   covariance_type=cov_type, max_iter=20, random_state=0))
                  for cov_type in ['spherical', 'diag', 'tied', 'full'])

n_estimators = len(estimators)

plt.figure(figsize=(3 * n_estimators // 2, 6))
plt.subplots_adjust(bottom=.01, top=0.95, hspace=.15, wspace=.05,
                    left=.01, right=.99)


for index, (name, estimator) in enumerate(estimators.items()):
    # Since we have class labels for the training data, we can
    # initialize the GMM parameters in a supervised manner.
    estimator.means_init = np.array([X_train[y_train == i].mean(axis=0)
                                    for i in range(n_classes)])

    # Train the other parameters using the EM algorithm.
    estimator.fit(X_train)

    h = plt.subplot(2, n_estimators // 2, index + 1)
    make_ellipses(estimator, h)

    for n, color in enumerate(colors):
        data = iris.data[iris.target == n]
        plt.scatter(data[:, 0], data[:, 1], s=0.8, color=color,
                    label=iris.target_names[n])
    # Plot the test data with crosses
    for n, color in enumerate(colors):
        data = X_test[y_test == n]
        plt.scatter(data[:, 0], data[:, 1], marker='x', color=color)

    y_train_pred = estimator.predict(X_train)
    train_accuracy = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100
    plt.text(0.05, 0.9, 'Train accuracy: %.1f' % train_accuracy,
             transform=h.transAxes)

    y_test_pred = estimator.predict(X_test)
    test_accuracy = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100
    plt.text(0.05, 0.8, 'Test accuracy: %.1f' % test_accuracy,
             transform=h.transAxes)

    plt.xticks(())
    plt.yticks(())
    plt.title(name)

plt.legend(scatterpoints=1, loc='lower right', prop=dict(size=12))


plt.show()

Relevant Link:

http://scikit-learn.org/stable/modules/generated/sklearn.mixture.GMM.html

posted @ 2017-09-26 23:31 郑瀚阅读(2190) 评论(0) 编辑收藏举报

刷新页面返回顶部

Han Zheng, Thinker and Doer

Welcome to contact me. Wechat：LittleHann

EM算法(Expectation Maximization Algorithm)初探

1. 通过一个简单的例子直观上理解EM的核心思想

0x1: 问题背景

0x2: 加入隐变量

0x3: EM初级版

0x4: EM进阶版

2. EM算法的引入

0x1: EM算法数学定义

0x2: 举一个实际的例子说明EM算法的推导

3. EM算法的收敛性

0x1: 定理1 - EM对模型参数的最大似然估计是单调递增的

4. EM算法在高斯混合模型（GMM）学习中的应用

0x1: 高斯混合模型定义

0x2: 高斯混合模型参数估计中的EM的算法

1. 明确隐变量，写出完全数据的对数似然函数

2. EM算法的E步：确定Q函数

3. 确定EM算法的M步

5. EM算法在思想上和K-means的异同点

0x1: 简单回顾K-means算法

0x2: K-means算法是EM算法的一个特例数学证明

0x3: k-means算法与由EM算法推导出的的关系

6. EM算法在高斯混合模型(GMM)学习中的应用

0x1: 利用GMM进行无监督聚类

公告